
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термин называется нераспределенным, Если он в данном суждении рассматривается не во всем объеме.Содержание книги
Поиск на нашем сайте
1. 2.
На основании рассмотрения соотношения распределенности S и Р можно составить следующую таблицу.
3.
Простые суждения находятся в определенных отношениях друг к другу, что мы можем использовать в процессе умозаключений В XI веке византийский логик Михаил Пселл предложил облегчить запоминание и преобразование суждений, введя так называемый «логический квадрат», у которого оказались свойства, считавшиеся магическими. Но суть «логического квадрата» проста. Если верхние углы квадрата обозначить символами общих суждений, соответственно нижние - символами частных, правые вершины - отрицательных, а левые утвердительных суждений, то получим в виде каждой стороны и диагонали квадрата определенное отношение между простыми категорическими суждениями. По этим отношениям можно делать умозаключение. Вертикальные линии теперь будут означать подчиненность нижних типов суждений верхним. У этих общих суждений А и Е выявляются отношения контрарности (противности). У отношений частных I и 0 совсем другое правило, называемое подпротивностъю (субконтрарностью). У суждений по диагоналям типов А и 0, 1 и Е отношения контрадикторности (противоречащие). Запомнив «логический квадрат», можно устанавливать истинность и ложность одних суждений по другим. То есть, если мы знаем, как установить истинность интересующего нас суждения, мы подставляем его в «логический квадрат» и «обкатываем». Если нашли возможность установить истинность или ложность хотя бы одного из четырех, у нас появляется право судить и об интересующем нас. По логическому квадрату можно преобразовывать общие в частные, утвердительные в отрицательные, и наоборот, не сомневаясь в той, что не превратим истинные в ложные. В «логическом квадрате» из истинности или ложности одного типа суждений с необходимостью следует истинность или ложность другого, но может быть и неопределенность, позволяющая также вскрывать логические ошибки по правилам квадрата.
Отношения подчинения. Из истинности общих суждений следует истинность и частных суждений того же качества: из истинности общеутвердительного следует истинность частноутвердительного, а из истинности Е следует истинность 0. Но из ложности общих 1 ложность частных не следует, частные Субконтрарные в этом случае могут быть как тоже ложными, так и истинными. Если суждение «Все дети доверчивы» - истинно, то с необходимостью это должно быть истинно и со отношению к части детей. Если каждый человек не может жить без воздуха, то и некоторые тоже. Но если неверно, что все люди от природы труженики,. то из этого не следует, что вообще нет тружеников от при роды, что Евангелие ошибается, сие надо еще доказать. Если ложь, что все не любят авторские песни, то отсюда никак. нельзя делать вывод, что ложно, будто некоторые не любят или любят, и это надо еще доказывать.
Как же происходит умозаключение по логическому квадрату.
I. 1)Если А (и), то Е (л), О (л), I (и). используя логический квадрат и метод логического отрицания из А (и) можем получить следующие истинные суждения: А(и) - > I (и) Например, Все кражи являются хищениями (А, и), значит «Некоторые кражи – являются хищениями»(I. и),
2). Если Е (и), то А (л), I (л), О(и) используя логический квадрат получаем Е (и) - > О (и) Например, Ни один лентяй не заслуживает похвалы (Е,.и), значит Некоторые лентяи не заслуживают похвалы» (О, и)
1) Если I (и), то А неопределенно, О неопределенно, Е (л) используялогический квадрат получаем. Из I (и) не можем получить истинные высказывания: Утверждения «Все цыгане живут оседло» или «Ни один цыган не живет оседло», то они неопределенны по своему содержанию . 2) Если О (и), то Е неопределенно, I неопределенно, а А (л) используя логический квадрат можно получить следующие выводы: О (и) -> неопределенно Например, «Некоторые преступления не являются умышленными» О (и),
II.Теперь рассмотрим возможные варианты умозаключений из ложных высказывания по логическому квадрату. Здесь возможны следующие случаи: 1) Если А (л), то, Е неопределенно, О истинно, I неопределенно. Используя логический квадрат можно получить следующие выводы. А (л) - > неопределенно Например, «Все правонарушения совершаются умышленно» (А, л),
2) Если Е (л) то,А неопределенно, I (и), О неопределенно. Используя логический квадрат можно получить следующий вывод: Е (л) -> неопределенно Например, «Ни один свидетель не говорит правды в суде» (Е, л.), 3) Если I (л), то А (л), О (и),Е (и). Используя логический квадрат и метод отрицания простых суждений можно получить следующий вывод. I (л) - > А (л), Например, «Часто наиболее надежные договоры заключаются между незнакомыми людьми» (I,л), следовательно «Все наиболее надежные договоры заключаются между незнакомыми людьми». (А,л),
4) Если О (л), то Е (л), I (и), А (и). Используя логический квадрат можно сделать следующие умозаключения: О (л) - > Е (л), Например, «Некоторые слова естественного языка являются бессмысленными» (О,л), следовательно, «Ни одно слово естественного языка не имеет смысла» (Е, л); Попробуем сделать умозаключение по логическому квадрату ««Числа суть величины VSAP
Сложные суждения, состоящие из двух и более суждений вступают в отношения, подобные простым. Эти отношения мы систематизировали с помощью логического квадрата и операции отрицания.. Сложные суждения образуются путем соединения простых с помощью логических союзов: ~ отрицание «неверно, что» ^ конъюнкция (грамматические союзы «и», «или», «но», «да») v - слабая дизъюнкция(«либо, либо» в значении и то, и то вместе); v - грамматические союзы «либо, либо..», «или, или..» в значении «что- одно из двух») è импликация (грамматический если, то», «когда,..тогда «); < -> эквиваленция «грамматические союзы, «если, только если, то», «тогда и только тогда, когда» По типу применяемых союзов все сложные суждения делятся на следующие виды, причем каждый из них имеет свою таблицу истинности.
I. Отрицание, в результате которого из простых суждений образуется сложное. Отрицание начинается со слов «Неверно, что…» Отрицание суждений – это логическая операция, состоящая в преобразовании логического содержания отрицаемого суждения, конечным результатом которого является формирование нового суждения, находящегося в отношении противоречия (контродикторности) к исходному. В результате отрицания получаем следующие эквивалентности. При отрицании к суждению добавляется «неверно, что»…. ~A равнозначно О ~O равнозначно А ~ Е равнозначно I ~I равнозначно Е
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.144.147 (0.011 с.) |





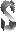

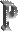
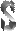
 Термин распределен, если он полностью включается в объем другого термина, а также, если он полностью исключается из объема другого термина или из части объема другого термина.
Термин распределен, если он полностью включается в объем другого термина, а также, если он полностью исключается из объема другого термина или из части объема другого термина.
 Распределены S и Р; 2. Распределены S и Р. 3. Распределен Р. 4.
Распределены S и Р; 2. Распределены S и Р. 3. Распределен Р. 4. Распределен S. 1. 2. 3. 4.
Распределен S. 1. 2. 3. 4.



