
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические операции и базовые элементы компьютераСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые высказывания. Истинность результирующих высказываний зависит от истинности исходных и использованных для их преобразования логических операций. „ Схемные элементы ЭВМ. Преобразование информации в ЭВМ осуществляется элементами (схемами) двух классов: - комбинационными; - последовательностными (схемами с памятью). Состояние выходов комбинационных схем однозначно определяется состояниями входов в данный момент времени. Состояние выходов в последовательных схемах определяется не только состоянием входов, но и внутренними состояниями, имевшими место в предыдущие моменты времени. Комбинационные схемы являются техническим аналогом булевых функций. Подобно тому, как сложная булева функция может быть получена суперпозицией более простых функций, так и комбинационная схема может строиться из более простых схем. Существует следующее определение — систему логических элементов, с помощью которых путем суперпозиции можно представить любую сколь угодно сложную комбинационную схему, называют функционально полной. Известны различные функционально полные системы элементов, но наибольшее распространение получили системы, использующие логические операции, выражаемые предлогами НЕ, и, или. Логический элемент компьютера — это часть электронной схемы, которая реализует элементарную логическую функцию. Логическими элементами компьютеров являются электронные схемы «И», «ИЛИ», «НЕ», «И-НЕ», «ИЛИ-НЕ» или другие (называемые также вентилями), а также триггер. Можно показать, что с помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода. Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Работу логических элементов описывают с помощью таблиц истинности. Рассмотрим логические операции и соответствующие им элементы логических схем. Конъюнкция. Соединение двух (или нескольких) высказываний в одно с помощью союза и (or) называется операцией логического умножения, или конъюнкцией. Эту операцию принято обозначать знаками «^, &» или знаком умножения «х». Сложное высказывание А ^ В истинно только в том случае, когда истинны оба входящих в него высказывания. Истинность такого высказывания задается табл.
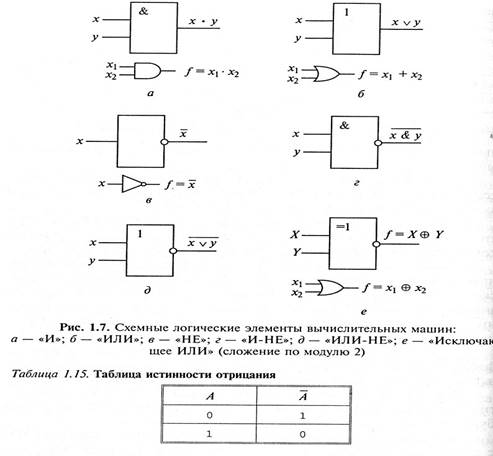
Логическая схема «И» реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных диаграммах схемы «И» с двумя входами представлено на рис. Единица на выходе схемы «И» будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет нуль, на выходе также будет нуль. Связь между выходом z этой схемы и входами х и у описывается соотношением z = x&y (читается как «х и у»). Операция конъюнкции на структурных схемах обозначается знаком «&». Дизъюнкция. Объединение двух (или нескольких) высказываний с помощью союза или (OR) называется операцией логического сложения, или дизъюнкцией. Эту операцию обозначают знаками «I, v» или знаком сложения «+». Сложное высказывание A v В истинно, если истинно хотя бы одно из входящих в него высказываний (см. табл. 1.14). В последнем столбце табл. 1.14 размещены результаты модифицированной операции ИЛИ — Исключающее или (XOR). Отличается от обычного или последней строкой (см. также рис. 1.7, е). Схема «ИЛИ» реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы «ИЛИ» будет единица, на ее выходе также будет единица. Условное обозначение на структурных схемах схемы «ИЛИ» с двумя входами представлено на рис. 1.7, б. Знак «1» на схеме происходит от классического обозначения дизъюнкции как «>=» (т. е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами х и у описывается соотношением z = x v у (читается как «х или у»).
Инверсия. Присоединение частицы НЕ (not) к некоторому высказыванию_ называется операцией отрицания (инверсии) и обозначается А (или А). Если высказывание А истинно, то В ложно, и наоборот (табл. 1.15) Схема «НЕ» (инвертор) реализует операцию отрицания. Связь между входом х этой схемы и выходом z можно записать соотношением z = х, где х читается как «не х» или «Инверсия х». Если на входе схемы «О», то на выходе «1», и наоборот. Условное обозначение на структурных схемах инвертора — на рис. 1.7, в. Вентили. Кроме схемных элементов, соответствующих перечисленным логическим операторам, в состав логических схем ходят комбинированные связки, именуемые вентилями, например, следующие. Схема «И-НЕ» состоит из элемента «И» и инвертора и осуществляет отрицание результата схемы «И» (табл. 1.16). Связь между выходом z и входами х и у схемы записывают как Таблица 1.16. Таблица истинности схем «И-НЕ», «ИЛИ-НЕ»
Схема «ИЛИ-НЕ» состоит из элемента «ИЛИ» и инвертора и осуществляет отрицание результата схемы «ИЛИ» (табл. 1.16). Связь между выходом z и входами хну схемы записывают как х v у, или «Инверсия х или у». Условное обозначение на структурных схемах схемы «ИЛИ-НЕ» с двумя входами представлено на рис. 1.7, д. Схема «Исключающее ИЛИ» (рис. 1.7, е) соответствует «сложению по модулю два» (см. также табл. 1.14). Следует отметить, что помимо операций и, или, не в алгебре высказываний существует ряд и других операций. Например, операция эквивалентности (эквиваленции) А ~ В (А = В, или A eqv В ) (табл. 1.17). Таблица 1.17. Таблицы истинности операций эквивалентности и импликации
Другим примером может служить логическая операция импликации или логического следования (А —> В, A IMP В)у иначе говоря, «если А, то В» (табл. 1.17). Высказывания, образованные с помощью логических операций, называются сложными. Истинность сложных высказываний можно установить, используя таблицы истинности. Например, истинность сложного высказывания ( Таблица 1.18. Таблица истинности высказывания (A&B)v(
Высказывания, у которых таблицы истинности совпадают, называются равносильными. Для обозначения равносильных высказываний используют знак «=» (А = В). Рассмотрим сложное высказывание (А ^ В) v ( Таблица 1.19. Таблица истинности выражения (А & В) v (
Если сравнить эту таблицу с таблицей истинности операции эквивалентности высказываний A v В(см. табл. 1.17), то можно увидеть, что высказывания (А ^ В) v (А ^ В) и А ~ В тождественны, т. е. (А ~ В) = (А л В) v (А л В). В алгебре высказываний можно проводить тождественные преобразования, заменяя одни высказывания равносильными им другими высказываниями. Свойства операций. Исходя из определений дизъюнкции, конъюнкции и отрицания, устанавливаются свойства этих операций и взаимные распределительные свойства. Приведем примеры некоторых из этих свойств:
Высказывания, образованные с помощью нескольких операций логического сложения, умножения и отрицания, называются сложными. Истинность всякого сложного высказывания устанавливается с помощью таблиц истинности. Сложные высказывания, истинные (true) для любых значений истинности входящих в них простых высказываний, называются тождественно-истинными. Наоборот, тождественно-ложными являются формулы, принимающие значение false для любых значений входящих в него простых высказываний. В табл. 1.20 приведено доказательство истинности дистрибутивного закона. Аналогичным образом могут быть доказаны и другие тождества.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1562; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.29 (0.008 с.) |

 , или «Инверсия х и у». Условное обозначение на структурных схемах схемы «И-НЕ» с двумя входами приведено на рис. 1.7, г.
, или «Инверсия х и у». Условное обозначение на структурных схемах схемы «И-НЕ» с двумя входами приведено на рис. 1.7, г.

 В
В
 ^
^ 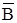 )определяется табл. 1.18.
)определяется табл. 1.18.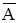 &
& 



