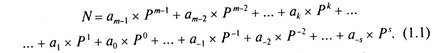Практическая работа №1-3 Представление информации в ЭВМ. Кодирование и подсчет количества информации.

Практическая работа №1-3 Представление информации в ЭВМ. Кодирование и подсчет количества информации.

ЦЕЛЬ РАБОТЫ

Приобретение навыков представления двоичной информации в ЭВМ

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Прочитать задания к работе, просмотреть все предложенные примеры решения задач и дополнительные задания к ним

2. Сформулировать условие и решить задачу.

3. Оформите отчет по самостоятельной работе, который должен содержать:

-титульный лист (см. приложение);

-условие задачи;

-решение;

-ответ.

3. ЗАДАНИЯ К РАБОТЕ.

Для выполнения этого задания потребуются некоторые сведения из теории и определения:

Системы счисления. Человек привык считать предметы десятками, сотнями: десять единиц образуют десяток, десять десятков — сотню, десять сотен — тысячу и т. д. Это — десятичная система счисления, которая не является единственно возможной (известна, например, двенадцатеричная система счисления).

Система счисления — способ именования и изображения чисел с помощью символов, имеющих определенные количественные значения. В зависимости от способа изображения чисел системы счисления делятся на:

• непозиционные;

• позиционные.

Непозиционные системы счисления. В такой системе цифры не меняют своего количественного значения при из­менении их расположения в числе.

Самый простой и очевидный пример — система счисления, где количество обозначается I (палочкой/единицей):

1 = I;

2 = I;

5 = IIIII;

10= IIIIIIIIII.

Пусть далее следующие символы (цифры в гипотетической системе счисления) соответствуют числам (в десятичной системе счисления):

Н - 1;

Л - 6;

Е - 12

* - 24;

Щ - 60;

S - 365,

и пусть есть правило, по которому число можно записать любой комбинацией таких символов, чтобы сумма обозначаемых ими чисел была равна заданному числу.

Тогда 444 можно записать по крайней мере двумя способами: SЩЕЛН (365 + 60+12 + 6+1); ЛН SЩЕ (6 + 1 + 365 + 60 + 12), т. е. SЩЕЛН = ЛН SЩЕ

Такая система счисления является непозиционной, так как цифры не меняют своего количественного значения при измене­нии их расположения в числе.

Позиционные системы счисления. В этом случае количественное значение каждой цифры зависит от ее места (позиции) в числе.

Десятичная система счисления является позиционной, так как значение каждой цифры зависит от ее места (позиции) в числе.

Например,

23 = 2 х 10 + 3;

32 = 3 х 10 + 2

и 23 не равно 32

Римская система счисления является смешанной, так как значение каждой цифры частично зависит от ее места (позиции) в числе. Так, в числах

VII

VI

IV

V обозначает 5, а I обозначает I. Но, с другой стороны, важно, как цифры расположены относительно друг друга:

VII = 5+1 + 1=7;

VI = 5+1=6; IV=5- 1=4.

Наиболее естественный способ представления числа в компьютерной системе заключается в использовании строки битов, называемой двоичным числом — числом в двоичной системе счисления (символ также может быть представлен строкой би­тов, или символа).

Основание позиционной системы счисления — количество (Р) различных цифр, используемых для изображения числа в позиционной системе счисления. Значения цифр лежат в пределах от 0 до Р-1.

В общем случае запись любого числа N в системе счисления с основанием Р будет представлять собой ряд (многочлен) вида: (1.1)

Нижние индексы определяют местоположение цифры в числе (разряд):

• положительные значения индексов — для целой части числа (т разрядов);

• отрицательные значения — для дробной (s разрядов). Максимальное целое число, которое может быть представлено в т разрядах:

N_max = Р^т - 1

Минимальное значащее, не равное 0 число, которое можно записать в s разрядах дробной части:

N_min = P^s

Имея в целой части числа т разрядов, а в дробной — s, можно записать P^m+s разных чисел

Двоичная система счисления (основание Р=2) использует для представления информации две цифры — 0 и 1.

Существуют простые правила перевода чисел из одной системы счисления в другую, основанные, в том числе, и на выражении (1.1).

Например, двоичное число 101110,101 равно десятичному числу 46,625:

101110,101₂= 1 х2⁵ + 0х2⁴+ 1 х2³+ 1 х2²+ 1 х2' + 0х2° +1 х 2^-1 + 0 х 2^-2 + 1 х 2^-3 = 46,625₁₀.

Практически перевод из двоичной системы в десятичную можно легко выполнить, надписав над каждым разрядом соответствующий ему вес и сложив затем произведения значений соответствующих цифр на их веса.

Например, двоичное число 01000001₂ равно 65₁₀. Действительно, 64 х 1 + 1 х 1 = 65.

Вес
Цифра

Таким образом, для перевода числа из позиционной системы счисления с любым основанием в десятичную систему счисления можно воспользоваться выражением (1.1).

Обратный перевод из десятичной системы счисления в систему счисления с другим основанием непосредственно по (1.1) затруднителен, поскольку все арифметические действия, предусмотренные этой формулой, следует выполнять в той системе счисления, в которую число переводится. Обратный перевод выполняется значительно проще, если предварительно преобразовать отдельно целую и дробную части выражения (1.1) к виду:

Алгоритм перевода числа из десятичной системы счисления в систему счисления с основанием Р, основанный на этих выражениях, позволяет оперировать числами в той системе счисле­ния, из которой число переводится, и может быть сформулиро ван следующим образом (при переводе смешанного числа следует переводить его целую и дробную части отдельно):

• для перевода целой части числа ее, а затем целые части получающихся частных от деления следует последовательно делить на основание Р до тех пор, пока очередная целая часть частного не окажется равной 0. Остатки от деления, записанные последовательно справа налево, образуют целую часть числа в системе счисления с основанием Р;

• для перевода дробной части числа ее, а затем дробные части получающихся произведений следует последовательно умножать на основание Р до тех пор, пока очередная дробная часть произведения не окажется равной 0 или не будет достигнута нужная точность дроби. Целые части произве­дений, записанные после запятой последовательно слева направо, образуют дробную часть числа в системе счисле­ния с основанием Р.

Пример 1 Пусть требуется перевести смешанное число (например, 46,625) из десятичной в двоичную систему счисления.

1. Переводим целую часть числа: 46: 2 = 23 (остаток 0);

23: 2 = 11 (остаток 1); 11: 2 = 5 (остаток 1); 5:2 = 2 (остаток 1); 2:2=1 (остаток 0); 1:2 = 0 (остаток 1).

Записываем остатки последовательно справа налево — 101110, т.е.

46₁₀= 101110₂.

2. Переводим дробную часть числа: 0,625x2= 1,250;

0,250x2 = 0,500;

0,500 х 2 = 1,000 (дробная часть равна 0 => стоп).

Записываем целые части получающихся произведений после запятой последовательно слева направо — 0,101, т. е.

0,625₁₀ = 0,101₂.

Окончательно: 46,625₁₀= 101110,101₂.

Пример 3

Сложение	101110 + 001011	Вычитание	101110 001011
Результат		Результат
У'множение	X 101 101101 000000 101101	Деление	101101 /101 01 010 0101
'Результат произведение)		Результат (частное)

 

Пример 4

Пример 5

Пример 6

ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ

Расскажите о позиционных и непозиционных системах исчисления

Назовите некоторые наиболее известные коды

В чем сущность двоичного кодирования звуковой информации

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Представление чисел в ЭВМ

В ЭВМ применяются две формы представления чисел:

• естественная форма, или форма с фиксированной запятой(точкой) - ФЗ (ФТ);

• нормальная форма, или форма с плавающей запятой (точкой) - ПЗ (ПТ).

Фиксированная запятая (точка). В форме представления с фиксированной запятой (точкой) числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.

Например, пусть числа представлены в десятичной системе счисления и имеют пять разрядов в целой части числа (до запятой) и пять — в дробной части (после запятой). Числа, записанные в такую разрядную сетку, имеют вид:

+00721.35500;

+00000.00328;

-10301.20260.

Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел.

Диапазон значащих чисел N в системе счисления с основа­нием Р при наличии т разрядов в целой части и s разрядов в дробной части числа (без учета знака числа) будет таким:

P^-s<N<P^m- Р^-s

Например, при Р=2, m= 10 и s = 6 числа изменяются в диапазоне 0,015 <N< 1024. Если в результате операции получится число, выходящее за допустимые пределы, произойдет переполнение разрядной сетки, и дальнейшие вычисления теряют смысл. В современных компьютерах естественная форма представления используется как вспомогательная и только для целых чисел.

В памяти ЭВМ числа с фиксированной точкой хранятся в трех форматах:

• полуслово — это обычно 16 бит или 2 байта;

• слово — 32 бита или 4 байта;

• двойное слово — 64 бита или 8 байтов.
Отрицательные числа с ФТ записываются в разрядную сетку в дополнительных кодах, которые образуются прибавлением единицы к младшему разряду обратного кода. Обратный код получается заменой единиц на нули, а нулей на единицы в прямом двоичном коде.

Плавающая запятая (точка). В форме представления с плавающей запятой (точкой) число изображается в виде двух групп цифр:

• мантисса;

• порядок.

При этом абсолютная величина мантиссы должна быть меньше 1, а порядок должен быть целым числом. В общем виде число в форме с плавающей запятой может быть представлено так:

N=±M x P^±r,

где М — мантисса числа (|М| < 1);

r — порядок числа (целое число);

Р — основание системы счисления.

Например, приведенные ранее числа в нормальной форме запишутся следующим образом:

+0,721355 х 10³;

+0,328 х 10^-3;

-0,103012026 х 10⁵.

Нормальная форма представления обеспечивает большой диапазон отображения чисел и является основной в современных компьютерах. Так, диапазон значащих чисел в системе счисления с основанием Р при наличии т разрядов у мантиссы и s разрядов у порядка (без учета знаковых разрядов порядка и мантиссы) будет:

Р^-т _х p-iP--\) <М<(\-Р~^т)х

При Р=2, m= 10 и s = 6 и = 22 и s= 10 диапазон чисел прости­рается примерно от 10^-300 до 10³⁰⁰. Для сравнения отметим, что количество секунд, которые прошли с момента образования планет Солнечной системы, составляет около 10¹⁸.

Следует заметить, что все числа с плавающей запятой хранятся в машине в так называемом нормализованном виде.

Нормализованным называют такое число, в старшем разряде мантиссы которого стоит единица (следовательно, для нормализованных двоичных чисел 0,5 < \М\ < 1).

Нормализованные, т. е. приведенные к правильной дроби,; числа:

10,35₁₀ = 0,1035₁₀ х 10²;

0,00007245₈ = 0,7245₈ х 8^-4;

F5C,9B₁₆ = 0,F5C9B₁₆xl6³.

Алгебраическое представление двоичных чисел. Для алгебраического представления чисел, т. е. для их представления с учетом знака, в вычислительных машинах используются специальные коды:

• прямой;

• обратный

• дополнительный.

При этом два последних кода позволяют заменить операцию вычитания на операцию сложения с отрицательным числом. Дополнительный код обеспечивает более быстрое выполнение операций, поэтому в ЭВМ применяется чаще именно он.

Знак числа обычно кодируется двоичной цифрой, при этом:

• код 0 означает знак + (плюс);

• код 1 означает знак - (минус). Прямой код числа N обозначим [N _лр ]. Пусть N= а₁, а₂, а₃,..., а_m, тогда:

. при N> 0 [N]_np = 0, а₁, а₂, а₃,..., а_m,

при N< 0 [N_np = 1, а₁, а₂, а₃,..., а_m,,

• при N = 0 имеет место неоднозначность [0]_пр = 0, 0... = 1, 0...

Если при сложении в ЭВМ оба слагаемых имеют одинако­вый знак, то операция сложения выполняется обычным путем. Если при сложении слагаемые имеют разные знаки, то сначала необходимо выявить большее по абсолютной величине число, из него произвести вычитание меньшего по абсолютной величине числа, и разности присвоить знак большего числа.

Выполнение операций умножения и деления в прямом коде осуществляется обычным образом, но знак результата определя­ется по совпадению или несовпадению знаков участвовавших в операции чисел.

Операцию вычитания в этом коде нельзя заменить операци­ей сложения с отрицательным числом, поэтому возникают слож­ности, связанные с займом значений из старших разрядов уменьшаемого числа. В связи с этим прямой код в ЭВМ почти не применяется.

Обратный код числа N обозначим [N]_о6р.

Пусть N = а₁, а₂, а₃,..., а_m, и а~ обозначает инверсию а, т. е. если а = 1, то а = 0, и наоборот. Тогда:

. при N> 0 [N]_обр = 0, а₁, а₂, а₃,..., а_m,

. при N < 0 [N]_o6p = 1, а_1~, а₂, а₃,..., а_m,

• при N=0 имеет место неоднозначность [0] _o6p = 0,00...0 =

= 1,11…1

Для того чтобы получить обратный код отрицательного чис­ла, необходимо все цифры этого числа инвертировать, т. е. в знаковом разряде поставить 1, во всех значащих разрядах нули заменить единицами, а единицы — нулями.

Например,

для N = 1011 [N]_obp = 0,1011;

для N= —1011 [N]= 1,1011. [N]_o6p = 1,0100.

Дополнительный код числа Nобозначим [N]_доп.

Пусть, как и выше, N= а₁, а₂, а₃,..., а_m и а обозначает вели­чину, обратную а (инверсию а), т. е. если а= 1, то а = 0, и наоборот. Тогда:

. при N> 0 [N]_доп = 0 ,а₁, а₂, а₃,..., а_m

- при N< 0 [N]_доп = 1, а₁, а₂, а₃,..., а_m + 0.00...1.

Для того чтобы получить дополнительный код отрицательно­го числа, необходимо все его цифры инвертировать и затем к младшему разряду прибавить единицу. В случае возникновения переноса из первого после запятой разряда в знаковый разряд к числу следует прибавить единицу в младший разряд.

Например,

дляN= 1011 [N]_доп = 0,1011;

для N =-1100 [N]_доп = 1,0100;

для N =-11010100 [N]_доп = 1,00101100;

для N=-0000 [N]_доп= 10,0000 = 0,0000 (1 исчезает). Неодно­значности в изображении 0 нет.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Прочитать МЕТОДИЧЕСКИЕ УКАЗАНИЯ
2. Нарисовать в тетради обозначения схемных элементов

3. Ответить на контрольные вопросы

3. ОФОРМИТЕ ОТЧЕТ, КОТОРЫЙ ДОЛЖЕН СОДЕРЖАТЬ:

-титульный лист (см. приложение);

-цель работы;

-порядок выполнения работы;

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Начало исследований в области формальной логики было по­ложено работами Аристотеля в IV в. до нашей эры. Однако строго формализованный подход к проблеме впервые был предложен Дж. Булем. В честь него алгебру высказывания называют булевой (булевской) алгеброй, а логические значения — булевы­ми (булевскими). Основу математической логики составляет алгебра высказываний. Алгебра логики используется при построе­нии основных узлов ЭВМ (дешифратор, сумматор, шифратор).

Алгебра логики оперирует с высказываниями. Под вы­сказыванием понимают повествовательное предложение, отно­сительно которого можно утверждать, истинно оно или ложно. Например, выражение «Расстояние от Москвы до Киева больше, чем от Москвы до Тулы» истинно, а выражение «5 < 2» — ложно.

Высказывания (логические переменные) принято обозначать буквами латинского алфавита (иногда — с индексами): А, В, С,..., X, Y, а, Ь, с,..., х, у, z, (х₁, х₂,..., х_i,...) и т. д. Если высказывание С истинно, это обозначается как С= 1 (С= t, true), а если оно ложно, то С= 0 (С = f, false).

Синтез и оптимизация схем

При построении схемы, реализующей произвольную таблицу истинности, каждый выход анализируется (и строится схема) от­дельно. Для реализации таблицы истинности с помощью логиче­ских элементов «И» достаточно рассмотреть только те строки таблицы истинности, которые содержат логические «1» в выход­ном сигнале. Строки, содержащие в выходном сигнале логический «0», в построении схемы не участвуют. Каждая строка, со­держащая в выходном сигнале логическую «1», реализуется схе­мой логического «И» с количеством входов, совпадающим с количеством входных сигналов в таблице истинности. Входные сигналы, описанные в таблице истинности логической «1», пода­ются на вход этой схемы непосредственно, а входные сигналы, описанные в таблице истинности логическим «0», подаются на вход через инверторы. Объединение сигналов с выходов схем, реализующих отдельные строки таблицы истинности, произво­дится с помощью схемы логического «ИЛИ». Количество входов в этой схеме определяется количеством строк в таблице истинно­сти, в которых в выходном сигнале присутствует логическая «1». Рассмотрим конкретный пример. Пусть необходимо реализо­вать таблицу истинности, приведенную в табл. 1.22.

Для построения схемы, реализующей сигнал у₁, достаточно рассмотреть строки, выделенные светлой штриховкой. Эти стро­ки реализуются сборкой (микросхемой) S₂ на рис. 1.10. Каждая строка реализуется своей схемой «И», затем выходы этих схем объединяются. Для построения схемы, реализующей сигнал у₂, достаточно рассмотреть строки, выделенные более темной штри­ховкой. Эти строки реализуются сборкой S₃. Инвертирование входов схемы осуществляется сборкой S₁.

Преобразования логических формул. Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упроще­ния формул или приведения их к определенному виду путем использования основных законов алгебры логики.

Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая по сравнению с исходной либо содержит меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содер­жит меньшее число вхождений переменных.

Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и соче­тательного законов и т. п.), тогда как другие преобразования ос­нованы на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъ­юнкции, свойств поглощения и склеивания, законов де Моргана и др.).

 

Практическая работа 6 -7-8. Регистры процессора. Память.

ЦЕЛЬ РАБОТЫ

Приобретение навыков работы с регистрами процессора. и памятью.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Прочитать методические указания 1, 2
2. Разобрать приведенные примеры 1, 2
3. Выполнить задания к работе 1 и 2
4. Ответить на контрольные вопросы 1, 2

Оформите отчет, который должен содержать:

- титульный лист (см. приложение);

-постановку задачи;

-формулировка варианта задания.

-размещение данных в ОЗУ.

-программа в форме таблицы

-последовательность состояний регистров ЭВМ при выполнении программы в режиме Шаг для одного значения аргумента.

-результаты выполнения программы для нескольких значений аргумента, выбранных самостоятельно.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ 1

Для решения с помощью ЭВМ некоторой задачи должна быть разработана программа. Программа на языке ЭВМ представляет собой последовательФзность команд. Код каждой команды определяет выполняемую операцию, тип

адресации и адрес. Выполнение программы, записанной в памяти ЭВМ, осуществляется последовательно по командам в порядке возрастания адресов команд или в порядке, определяемом командами передачи управления.

Для того чтобы получить результат выполнения программы, пользователь должен:

□ ввести программу в память ЭВМ;

□ определить, если это необходимо, содержимое ячеек ОЗУ и РОН, содержащих исходные данные, а также регистров 1R и BR;

□ установить в PC стартовый адрес программы;

□ перевести модель в режим Работа.

Каждое из этих действий выполняется посредством интерфейса модели, описанного в главе 8. Ввод программы может осуществляться как в машинных кодах непосредственно в память модели, так и в мнемокодах в окно Текст программы с последующим ассемблированием.

Цель настоящей лабораторной работы — знакомство с интерфейсом модели ЭВМ, методами ввода и отладки программы, действиями основных классов команд и способов адресации. Для этого необходимо ввести в память ЭВМ и выполнить в режиме Шаг некоторую последовательность команд (опреде­ленную вариантом задания) и зафиксировать все изменения на уровне про­граммно-доступных объектов ЭВМ, происходящие при выполнении этих команд.

Команды в память учебной ЭВМ вводятся в виде шестиразрядных десятич­ных чисел (см. форматы команд на рис. 8.3, коды команд и способов адреса­ции в табл. 8.2—8.4).

В настоящей лабораторной работе будем программировать ЭВМ в машинных кодах.

Пример 1

Дана последовательность мнемокодов, которую необходимо преобразовать в машинные коды, занести в ОЗУ ЭВМ, выполнить в режиме Шаг и зафиксировать изменение состояний программно-доступных объектов ЭВМ (табл. 9.1).

 

					Таблица 9.1.	Команды и коды
Последовательность	Значения
Команды	RD#20	WR30	ADD	#5		WR@30		JNZ 002
Коды	21 1 020	22 0 030	23 1			22 2 030		12 0002

 

Введем полученные коды последовательно в ячейки ОЗУ, начиная с адреса 000. Выполняя команды в режиме Шаг, будем фиксировать изменения про­граммно-доступных объектов (в данном случае это Асе, PC и ячейки ОЗУ 020 и 030) в табл. 9.2.

Таблица 9.2. Содержимое регистров

 

PC	Асc	М(30)	М(20)	PC	Асc	М(30)	М(20)

Задание 1

1. Ознакомиться с архитектурой ЭВМ

2. Записать в ОЗУ "программу", состоящую из пяти команд— варианты задания выбрать из табл.. Команды разместить в последовательных ячейках памяти.

3. При необходимости установить начальное значение в устройство ввода IR.

4. Определить те программно-доступные объекты ЭВМ, которые будут изменяться при выполнении этих команд.

№	IR	Команда 1	Команда 2	Команда 3	Команда 4	Команда 5
		IN	MUL #2	WR10	wr @10	JNS 001
	X	RD #17	SUB #9	WR16	WR @16	JNS 001
		IN	ADD #16	WR8	WR @8	JS 001
	X	RD #2	MUL #6	WR 11	WR @11	JNZ 00
		IN	WR8	DIV #14	WR @8	JMP 002
	X	RD #4	WR 11	RD @11	ADD #330	JS 000
		IN	WR9	RD @9	SUB#1	JS 001
	X	RD 4	SUB #8	WR8	WR @8	JNZ 001
		IN	ADD #12	WR 10	WR @10	JS 004
	X	RD 4	ADD #15	WR 13	WR @13	JMP 001
		IN	SUB #308	WR11	WR @11	JMP 001
	X	RD #988	ADD #19	WR9	WR @9	JNZ 001
		IN	WR11	ADD 11	WR @11	JMP 002
	X	RD #5	MUL #9	WR10	WR @10	JNZ 001

5. Выполнить в режиме Шаг введенную последовательность команд, фиксируя изменения значений объектов, определенных в п. 4, в таблице (см. форму табл. 9.2).

6. Если в программе образуется цикл, необходимо просмотреть не более двух повторений каждой команды, входящей в тело цикла.

Таблица Варианты задания 1

Контрольные вопросы 1

1. Из каких основных частей состоит ЭВМ и какие из них представлены
в модели?

2. Что такое система команд ЭВМ?

3. Какие классы команд представлены в модели?

4. Какие действия выполняют команды передачи управления?

5. Какие способы адресации использованы в модели ЭВМ? В чем отличие между ними?

6. Какие ограничения накладываются на способ представления данных модели ЭВМ?

7. Какие режимы работы предусмотрены в модели и в чем отличие между ними?

8. Как записать программу в машинных кодах в память модели ЭВМ.

9. Как просмотреть содержимое регистров процессора и изменить содермое некоторых регистров?

10. Как просмотреть и, при необходимости, отредактировать содержи ячейки памяти?

11 Как запустить выполнение программы в режиме приостановки работы
после выполнения каждой команды?

12 Какие способы адресации операндов применяются в командах ЭВМ?

13 Какие команды относятся к классу передачи управления?

МЕТОДИЧЕСКИЕ УКАЗАНИЯ 2. ПРОГРАММИРОВАНИЕ РАЗВЕТВЛЯЮЩЕГОСЯ ПРОЦЕССА

Для реализации алгоритмов, пути в которых зависят от исходных данных, используют команды условной передачи управления.

Пример 2

В качестве примера (несколько упрощенного по сравнению с заданиями практической работы № 3) рассмотрим программу вычисления функции

причем х вводится с устройства ввода IR, результат у выводится на OR. Граф-схема алгоритма решения задачи показана на рис.

В данной практической работе используются двухсловные команды с непо­средственной адресацией, позволяющие оперировать отрицательными чис­лами и числами по модулю, превышающие 999, в качестве непосредственного операнда.

Оценив размер программы примерно в 20—25 команд, отведем для области данных ячейки ОЗУ, начиная с адреса 030. Составленная программа с комментариями представлена в виде табл. 9.4.

Таблица Пример программы

Адрес	Команда	Примечание
	Мнемокод	Код
	IN	01 0 000	Ввод х
	WR 30	22 0 030	Размещение х в ОЗУ(ОЗО)
	SUB #16	24 1016	Сравнение с границей — (х -16)
	JS 010		Переход по отрицательной разности
	RD 30	21 0 030	Вычисления по первой формуле
	SUB #11	24 1011
	WR 31	22 0 031
	MUL 31	25 0 031
	SUB #125	24 1 125
	JMP 020	10 0 020	Переход на вывод результата
	RD 30	21 0 030	Вычисления по второй формуле
	MUL 30	25 0 030
	WR 31	22 0 031
	RD 30	21 0 030
	MUL #72	25 1 072
	ADD 31	23 0 031
	ADI 106400	43 0 000
	DIVI 100168	46 0 000
	OUT	02 0 000	Вывод результата
	HLT	09 0 000	Стоп

Задание 2

1. Разработать программу вычисления и вывода значения функции:

F_i(x), при х>=а,

Fj(x) при x< а,

для вводимого из IR значения аргумента х. Функции и допустимые пре­делы изменения аргумента приведены в табл. 9.5, варианты заданий — в табл. 9.6.

2. Исходя из допустимых пределов изменения аргумента функций (табл. 9.5) и значения параметра а для своего варианта задания (табл. 9.6) выделить на числовой оси Ох области, в которых функция у вычисляется по представленной в п. 1 формуле, и недопустимые значения аргумента. На недопустимых значениях аргумента программа должна выдавать на OR максимальное отрицательное число: 199 999.

3. Ввести текст программы в окно Текст программы, при этом возможен набор и редактирование текста непосредственно в окне Текст программы

или загрузка текста из файла, подготовленного в другом редакторе.

4. Ассемблировать текст программы, при необходимости исправить синтаксические ошибки.

5. Отладить программу. Для этого:

а) записать в IR значение аргумента х > а (в области допустимых значений);

б) записать в PC стартовый адрес программы;

в) проверить правильность выполнения программы (т. е. правильность результата и адреса останова) в автоматическом режиме. В случае наличия ошибки выполнить пп. 5, г и 5, д; иначе перейти к п. 5, е;

г) записать в PC стартовый адрес программы;

д) наблюдая выполнение программы в режиме Шаг, найти команду, являющуюся причиной ошибки; исправить ее; выполнить пп. 5, а — 5, в;

е) записать в IR значение аргумента х < а (в области допустимых значений); выполнить пп. 5, б и 5, в;

ж) записать в IR недопустимое значение аргумента х и выполнить пп. 5, 6 и 5, в.

6. Для выбранного допустимого значения аргумента х наблюдать выполнение отлаженной программы в режиме Шаг и записать в форме табл. 9.2 содержимое регистров ЭВМ перед выполнением каждой команды.

Контрольные вопросы 2

1. Как работает механизм косвенной адресации?

2. Какая ячейка будет адресована в команде с косвенной адресацией через
ячейку 043, если содержимое этой ячейки равно 102 347?

3. Как работают команды передачи управления?

4. Что входит в понятие "отладка программы"?

5. Какие способы отладки программы можно реализовать в модели?

 

ЦЕЛЬ РАБОТЫ

Приобретение навыков работы с регистрами процессора. и памятью.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Прочитать методические указания 1, 2
2. Разобрать приведенные примеры 1, 2
3. Выполнить задания к работе 1 и 2
4. Ответить на контрольные вопросы 1, 2

Оформите отчет, который должен содержать:

- титульный лист (см. приложение);

-постановку задачи;

-формулировка варианта задания.

-размещение данных в ОЗУ.

-программа в форме таблицы

-последовательность состояний регистров ЭВМ при выполнении программы в режиме Шаг для одного значения аргумента.

-результаты выполнения программы для нескольких значений аргумента, выбранных самостоятельно.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ 1.

ПримерЗ

Разработать программу вычисления суммы элементов массива чисел С], С₂,..., С„. Исходными данными в этой задаче являются: п — количество суммируемых чисел и С_х, С₂,..., С„ — массив суммируемых чисел. Заме­тим, что должно выполняться условие п > 1, т. к. алгоритм предусматривает, по крайней мере, одно суммирование. Кроме того, предполагается, что сумми­руемые числа записаны в ОЗУ подряд, т. е. в ячейки памяти с последователь­ными адресами. Результатом является сумма S.

Составим программу для вычисления суммы со следующими конкретными параметрами: число элементов массива— 10, элементы массива расположены в ячейках ОЗУ по адресам 040, 041, 042,..., 049. Используемые для решения задачи промежуточные переменные имеют следующий смысл: A_t — адрес числа С,, i е {l, 2,..., 10}; ОЗУ(A_t) — число по адресу A_t, S — текущая сум­ма; к — счетчик цикла, определяющий число повторений тела цикла.

Распределение памяти таково. Программу разместим в ячейках ОЗУ, начиная с адреса 000, примерная оценка объема программы — 20 команд; промежу­точные переменные: А_г — в ячейке ОЗУ с адресом 030, к — по адресу 031, S — по адресу 032. ГСА программы показана на рис. 9.2, текст программы с комментариями приведен в табл. 9.7.

Адрес	Команда	Примечание
	RD #40	Загрузка начального адреса массива 040
	WR 30	в ячейку 030
	RD #10	Загрузка параметра цикла к = 10 в ячейку 031
	WR 31
	RD #0	Загрузка начального значения суммы S = 0
	WR 32	в ячейку 032
	Ml: RD 32	Добавление
	ADD @30	к текущей сумме
	WR 32	очередного элемента массива
	RD30	Модификация текущего
	ADD #1	адреса массива
	WR 30	(переход к следующему адресу)
	RD 31	Уменьшение счетчика
	SUB #1	(параметра цикла)
	WR 31	на1
	JNZ Ml	Проверка параметра цикла и переход при к ■*■ 0
	RD 32	Вывод
	OUT	результата
	HLT	Стоп

Задание 3

1. Написать программу определения заданной характеристики последовательности чисел С₁, С₂,..., С_п. Варианты заданий приведены в табл. 9.8.

2. Записать программу в мнемокодах, введя ее в поле окна Текст программы.

3. Сохранить набранную программу в виде текстового файла и произвести ассемблирование мнемокодов.

4. Загрузить в ОЗУ необходимые константы и исходные данные.

Отладить программу