
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теретико – ігрова модель ризикуСодержание книги
Поиск на нашем сайте
Критерії обґрунтування прийняття рішень Для дослідження ситуацій, в яких маркетингове рішення приймається за умов невизначеності, конфліктності й зумовленого ними ризику, використовують схему гри з економічним середовищем, яке може перебувати в одному з n взаємовиключних станів θј. Матриця гри (платіжна матриця) записується у вигляді функціонала оцінювання F+ (з додатним інгредієнтом), елементами якого fkj+ (k =1,…, m; j = 1,…, n) є кількісні оцінки рішення (стратегії) sk є S =(s1,s2,…, s m) за умови, щоекономічне середовище перебуває в стані θј є Θ = (θ1., θ2,,…, θn) F + = || fkj+ ||. Розрахунок значень fkj проводиться з урахуванням можливого рівня попиту на товар, формування ціни на одиницю продукції зі змінними і сталими витратами, можливим дефіцитом або перевиробництвом продукції. Тоді обґрунтування прийняття оптимального, раціонального (найбільш ефективного, найменш ризикованого) рішення проводиться за допомогою низки спеціальних критеріїв
1) ІС1: характеризується заданим розподілом апріорних імовірностей станів θј економічного середовища Р = (р1, р2.... рn) = (р(θ1), р(θ2),..., р(θn)), ∑ рj = 1, j = 1,…, n. Критерій Байєса – дляфункціонала оцінювання F+ (значень прибутку, виграшу, ефективності, корисності) оптимальна стратегія skо визначається умовою: B+ (skо; P) = Критерій мінімальної дисперсії – оптимальна стратегія skо визначається умовою: D- (skо;P) = Критерій мінімальної семі варіації – оптимальна стратегія skо визначається умовою: SV- (skо;P) = де αk = (αк1, αк2,..., αkn) – вектор індикаторів несприятливих відхилень для рішення sk відносно оцінки B+ (sk;P): αk =1 вразі сприятливого відхилення: (fkj+ - B+ (sk;P)) ≥ 0, і αk =0 в разі несприятливого відхилення: (fkj+ - B+ (sk;P)) <0. Критерій мінімального коефіцієнта варіації – оптимальна стратегія skо визначається умовою: СV- (skо;P) = де СV-(sk;P) = σ-(sk;P) / B+ (sk;P), σ-(sk;P) = Критерій мінімального коефіцієнта семі варіації –оптимальна стратегія skо визначається умовою: СSV- (skо;P) = де СSV-(sk;P) = SSV (sk;P) / B+ (sk;P), SSV (sk;P) =
2) ІС2: існує можливість оцінювання параметрів (числових характеристик), які характеризують розподіл апріорних ймовірностей, на підставі статистичної інформації перевіряється гіпотеза щодо класу функцій розподілу і будується вектор Р ^=(р1^ р2^;....; рn). 3) ІС3: відомі співвідношення пріоритету стосовно станів θј економічного середовища: рі1 ≥ рі2 ≥... ≥ ріn. перші оцінки Фішберна – оцінки p^іj апріорних імовірностей pіj, будуються у вигляді спадноїгеометричної прогресії: pіj ≈ p^іj = 4) ІС4: за умов повної невизначеності щодо закону розподілу ймовірностей Р (Θ = θј) використовується принцип Бернуллі – Лапласа: pj ≈ p^ j =1/n, j = 1,…, n (3.7) 5) ІС5: характеризується антагоністичними інтересами суб’єкта прийняття рішень (СПР) та економічного середовища, тобто конфліктом між ними, а основною стратегією для СПР є забезпечення гарантованого результату. Критерій Вальда (безризиковий за ситуації, де ризикувати недоцільно) – оптимальна стратегія skо визначається умовою: fko+ = Критерій Севіджа використовує матрицю ризику (невикористаних можливостей), яка будується так: · для кожного стану ЕС знаходиться · визначається rkj- = · оптимальна стратегія skо визначається умовою: rko- = 6) ІС6: характеризується наявністю факторів, що зумовлюють “проміжну” інформаційну ситуацію між ІС1 та ІС5 , використовує коефіцієнт λ є[0;1] – коефіцієнт схильності – несхильності до ризику. Критерій Гурвіца є зваженою комбінацією найкращого та найгіршого факторів для часткового антагонізму ЕС і СПР, оптимальна стратегія skо визначається умовою: G+(sko; λ) = Модифікований критерій: оптимальна стратегія skо визначається умовою: Ф+(sko;Р;λ)= де за величину Risk (sk; Р) можна використовувати σ-(sk ;P) або SSV(sk;P). Критерій Ходжеса – Лемана дає змогу використати всю наявну інформацію СПР, а оптимальна стратегія skо визначається умовою: HL+ (sko;Р; λ) = Практикум: Аналіз ризиків за умов розробки нового товару Розв’язування задач. Задача: Видавництво “Навігатор” готує до друку підручник “Маркетинг”, який буде цікавим не тільки для студентів і викладачів, але й стане в нагоді практикам. Якою повинна бути ціна книги? Якісний папір, суперобкладинка привернуть увагу потенційного покупця, але це призведе до збільшення ціни, та й бібліотеки надають перевагу книгам у жорстких обкладинках. Практиків більше цікавить видання з більшою практичною спрямованістю. Маркетологи видавництва запропонували видати пробний наклад (1000 примірників) у таких версіях: - А: підручник “Маркетинг” у жорсткій обкладинці; - В: підручник “Маркетинг” у м’якій обкладинці; - С: “Маркетинговий тренінг” у м’якій обкладинці. Якщо видавати всі ці варіанти, то вартість примірника зростатиме за рахунок додавання низки технологічних операцій заключного циклу. Потрібно змоделювати цю ситуацію для вибору оптимального рішення щодо видання підручника. Основним критерієм вибору кращого варіанта є максимізація прибутку, який можна розрахувати за такою формулою: П = Д – В = Ц · К – (ЗЗВ + ФВ) = Ц · К – (ЗВ · К + ФВ), де Д – виручка від реалізації продукції; В – повні витрати підприємства, що дорівнюють сумі загальних змінних витрат (ЗЗВ) та фіксованих витрат (ФВ) = 20000 грн.; ЗВ – змінні витрати на одиницю продукції (відповідно 15 грн. для А, 13 грн. для В, 14 грн. для С); К – кількість одиниць проданого товару; Ц – ціна одиниці продукції.
Значення умовного прибутку для кожного варіанта можливого попиту наведено в таблиці Умовний прибуток від реалізації книги “Маркетинг”
Приклад розрахунку умовного прибутку варіанта В можливого попиту в 3000 шт: П = 20 · 3000 – (13·3000 +20000) = 60000 –59000 =1000(грн.) Наступним кроком є аналіз отриманого функціонала оцінювання - значень умовного прибутку - за критеріями Байєса, Вальда, Севіджа.
ВА = 19000 · 0,3 + 45000 · 0,5 + 71000 · 0,2 = 42100 (грн), ВВ = 1000 · 0,3 + 15000 · 0,5 + 22000 · 0,2 = 12200 (грн), ВС = 10000 · 0,3 + 40000 · 0,5 + 57000 · 0,2 = 34400 (грн). За критерієм Байєса кращим є варіант А.
SV- (skо;P) = SSV (sk;P) = SV-1 = (19000 – 42100)2 · 0,3 = 160083000, SSV1 = SV-2 = (1000 – 12200)2 · 0,3 = 376320000, SSV2 = SV-3 = (10000 – 34400)2 · 0,3 = 178608000, SSV1 = За критерієм мінімальної семі варіації кращим є варіант В.
СSV-(sk;P) = SSV (sk;P) / B+ (sk;P) СSV-1= SSV 1 / B+ 1 = 12652,39 / 42100 = 0,3005, СSV2 = SSV 2 / B+ 2 = 6134,49 / 12200 = 0,50 28, СSV-3 = SSV 3 / B+ 3 = 13364,43 / 34400 = 0,3885 За критерієм мінімального коефіцієнта семі варіації кращим є варіант А.
За критерієм Вальда кращим є варіант А.
rko- =
R- =
Мax 1900 5000 71000 За критерієм Севіджа кращим є варіант А.
G+(sko; λ) = Видавництво планує виходити на сформований ринок, тобто слід очікувати наявність конкуренції, але в не досить жорсткій формі, тобто коефіцієнт схильності до ризику λ G+1 =[(1 – λ) · max f1j+ + λ · min f1j+ ] = (1 – λ)··45000 + λ·1900 = 45000 -26000·λ; G+2 =[(1 – λ) · max f2j+ + λ · min f2j+ ] = (1 – λ)··22000 + λ·1000 = 22000 -21900·λ; G+3 =[(1 – λ) · max f3j+ + λ · min f3j+ ] = (1 – λ)··57000 + λ·10000 = 57000 -47000·λ.
Будуємо лінії Гурвіца (рис.13) в системі координат з віссю Оλ і відповідними вертикалями – лініями максимальних і мінімальних значень G+(sk; λ) в точках О і 1. Положення ліній Гурвіца вказує, що кращими для СПР будуть перше і третє рішення, причому для певного значення λ ці рішення будуть рівнозначними: 57000 - 47000·λ. = 45000 - 26000·λ, 21000 λ =12000, λ =12/21 =4/7 ≈ 0,57. Для СПР,схильного до ризику з коефіцієнтом λ
Рис.13. Положення ліній Гурвіца. Тема 3.3: Загальна ієрархічна модель
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.118.151 (0.009 с.) |

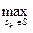 B+ (sk; P) =
B+ (sk; P) = 
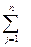 рj · fkj, k =1,…,m. (3. 1)
рj · fkj, k =1,…,m. (3. 1)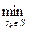 D-(sk;P) =
D-(sk;P) = 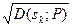 .
.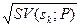 .
.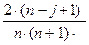 , j = 1,…, n. (3.6)
, j = 1,…, n. (3.6)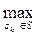 fk+ =
fk+ = 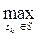 (
(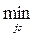 fkj+ ), j=1,…, n. (3.8)
fkj+ ), j=1,…, n. (3.8)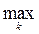 fk+,
fk+,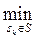 rk- =
rk- = 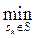 (
(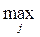 rkj-), j =1,…, n. (3.9)
rkj-), j =1,…, n. (3.9)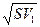 = 12652,39;
= 12652,39;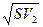 = 6134,49;
= 6134,49;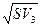 =13364,43;
=13364,43;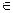 [ 0,4; 0,6 ]. Тоді
[ 0,4; 0,6 ]. Тоді



