
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Об'єктивні маркетингові ризикиСодержание книги
Поиск на нашем сайте
Ризик у маркетингу Маркетингова діяльність спрямована на визначення, аналіз і врахування факторів, які впливають на процеси виробництва продукції та її просування на ринку. В ході прийняття рішення про вибір стратегії і тактики розвитку, планування виробничо - збутової і фінансової діяльності практично неможливо з повною достовірністю стверджувати, що виконано аналіз всієї необхідної інформації, що враховані всі фактори, які мають вплив на розвиток кон'юнктури конкретних товарних ринків. З іншого боку, реалізація маркетингових заходів здійснюється в ринковому середовищі, стан якого безперервно змінюється під впливом багатьох різноспрямованих факторів, які у своїй більшості не залежать від дій конкретного підприємства. З цих причин важливі маркетингові рішення приймаються на основі неповної, неточної та суперечливої інформації, тобто в умовах ризику. Зрозуміло, що для раціональної діяльності суб’єкта прийняття рішень важливе значення має запобігання можливих невдалих результатів господарювання в перспективі чи виправлення або компенсація отриманих збитків.
Під ризиком у маркетингу слід розуміти загрозу понесення збитків або недоотримання прибутків у результаті реалізації конкретних рішень чи видів виробничо-збутової діяльності, що спираються на рекомендації маркетингу. Існуючі класифікації в основному виділяють маркетинговий ризик як одну зіскладових господарського (підприємницького) ризику. У складі маркетингових ризиків окремо виділяють: -конкурентний ризик, -ризик неприйняття продукції споживачами, -ризик неадекватної оцінки місткості ринку, -ризик прийняття неправильних маркетингових рішень, -ризик. пов'язаний зі змінами ситуації на ринку в період між його аналізом і прийняттям маркетингових рішень, що спираються на результати аналізу, тощо. Маркетингові ризики проявляються у вигляді нереалізації або зменшення обсягів реалізації продукції та зниженні цін на неї, наслідком чого є недоотримання прибутку або збитки, і загалом спричиняються:
Систематизація маркетингових ризиків і визначення факторів, що їхспричиняють, щодо конкретної ринкової ситуації необхідні для визначення процедур цілеспрямованого їх аналізу з метою розробки заходів, спрямованих на запобігання, зменшення або компенсацію ризику різних видів маркетингової діяльності. Систему маркетингових ризиків наведено на рис. 1. Детальний аналіз окремих маркетингових ризиків, а також факторів, що їх спричиняють, слід виконувати виходячи із завдань і функцій маркетингу, які, втім, є різними для стратегічного і оперативного маркетингу (перший більшою мірою співвідноситься з аналізом і визначенням стратегічних перспектив розвитку підприємства, другий – із заходами активного впливу на споживачів, посередників, товари, ринки тощо.
Рис.1. Загальна схема маркетингових ризиків
Принципи управління ризиком Управління ризиком має забезпечити оптимальне для підприємця співвідношення результатів економічної діяльності та ризику, яким вона обтяжена. Необхідною умовою розв'язання проблеми ризику є чітке усвідомлення цілей діяльності фірми. Виходячи з конкретних цілей, слід здійснювати збирання, обробку та аналіз інформації про зовнішнє середовище, про внутрішні показники фінансової, виробничої, комерційної діяльності фірми в минулому та в поточному періоді, а також прогнози щодо майбутнього. Управління ризиком у широкому сенсі — це процес виявлення J й оцінювання ризиків, а також вибір методів та інструментів управління для оптимізації ризику. Це необхідність використовувати в управлінській діяльності різноманітні підходи, процеси, заходи, які дають змогу певною мірою (наскільки це можливо) прогнозувати можливість настання ризикованих подій і домагатися зниження ступеня ризику до допустимих меж.
Необхідно визначити основні принципи процесу управління ризиками: принцип максимізації, який передбачає прагнення найширшого аналізу можливих причин і чинників виникнення ризику, тобто цей принцип наголошує необхідність зведення рівня невизначеності до мінімуму. принцип мінімізації означає, що управлінці намагаються звести до мінімуму, по-перше, спектр можливих ризиків, і, по-друге, мінімізувати рівень впливу ризику на свою діяльність. принцип адекватності реакції полягає в необхідності адекватно і швидко реагувати на зміни, які можуть призвести до виникнення ризику. принцип прийняття — управлінці (підприємці) можуть прийняти на себе лише обґрунтований ризик. Таблиця рішень Приймаючи рішення щодо способу управління ризиком, слід, насамперед, ураховувати можливий рівень збитків та ймовірність реалізації певного типу ризику (див. табл. 1). Класифікуючи ризики за ймовірністю їхньої реалізації та обсягів можливих збитків, можна вирізнити 2 граничні типи: 1. Ризики, що спричинюють окремі незначні збитки і за умов рі→1. 2. Ризики, наслідком яких є катастрофічні за обсягом збитки, імовірність реалізації яких незначна. Якщо в першому випадку доцільним є прийняття ризику з його оптимізуванням шляхом створення резервів коштів, то другий випадок є класичним прикладом ризику, який доцільно передавати страховику (в окремих випадках доцільно застосовувати розподіл ризику). Більшість ризиків, які загрожують економічній діяльності, є проміжними варіантами порівняно з наведеними вище. Природно, що кожна компанія може прийняти свою градацію рівнів збитків та ймовірностей збитків на підставі досліджень та експертних оцінок і будувати свою таблицю рішень. В реальному житті доцільно поєднувати окремі способи зниження ризику, комбінуючи зовнішні та внутрішні методи оптимізації ризику.
Рис. 2. Градація зон ризику Таблиця рішень
Практикум 1: Якісний аналіз ризику Статистичний метод Цей методбазується на аналізі коливань оцінюваного показника І (величини втрат) за певний період. Залежно від результативності дій за цей період, діяльність підприємства відносять до однієї з п'яти областей ризику: безризикова область, область мінімального ризику, область підвищеного ризику, область критичного ризику, область неприпустимого ризику. Віднесення результатів діяльності до тієї чи іншої області ризику виконується залежно від рівня втрат: - у без ризиковій області втрати відсутні; - в області мінімального ризику втрати не перебільшують чистого прибутку; - в області підвищеного ризику втрати вищі за чистий прибуток, але менші, ніж валовий дохід; - в області критичного ризику втрати вищі за валовий дохід, але менші, ніж виторг від реалізації продукції; - в області неприпустимого ризику втрати можна зіставити з розміром власних коштів підприємств. Для кількісної оцінки областей ризику вводять поняття коефіцієнта ризику який характеризує рівень втрат (наприклад, втратам у розмірі половини чистого прибутку відповідає коефіцієнт ризику 0,125, а втратам усього чистого прибутку - 0,25 і дозволяє вести кількісну оцінку ризику. Так, у зазначених Відповідно до інших підходів коефіцієнт ризику може бути розрахований як відношення втрат (різниці між запланованими і фактичними результатами) до запланованого результату.
Цей метод дає досить точні результати оцінювання ризику за умов дотриманні трьох основних вимог: - наявність достатнього обсягу достовірної статистичиої інформації даних не менше ніж за 3-5 попередніх періодів господарювання; - наявність чітко виражених тенденцій змін ризику в минулому і в поточний період; - виявлені тенденції змін оцінюваного показника будуть зберігатися і в майбутньому (це може бути за аналогічних умов господарювання в аналізованому і прогнозованому періодах). Різновидом статистичного методу є метод Монте-Карло, який за допомогою імітаційного аналізу дозволяє встановлювати ймовірності зміни оцінюваних характеристик проекту для можливих несподіваних ризикових (кризових) ситуацій. Метод аналогій Для аналізу ризику, яким може бути обтяжений новий проект, доцільно вивчити дані щодо наслідків впливу несприятливих чинників ризику стосовно близьких за сутністю раніше виконуваних проектів. У цій сфері діяльності найбільшу ініціативу виявляють страхові компанії. У використанні аналогів застосовують бази даних і знань щодо чинників ризику: Ці бази будуються на матеріалах із літературних джерел, пошукових робіт, моніторингу,шляхом опитування фахівців, менеджерів проектів тощо. Використовуючи відповідний математичний апарат, одержані дані обробляють з метою виявлення залежностей та врахування потенційного ризику в реалізації нових проектів.
Розв’язання 1). Результуючий коефіцієнт упевненості, знайдений за правилами (2.1), дорівнює -0,38:
Отримане значення свідчить про те, що є слабкі докази несприятливого розвитку подій. 2). Однак для прийняття рішень, що спираються на результати оцінки ризику, даного розрахунку недостатньо. Потрібні додаткові дослідження, які, можливо, потребують урахування більшої кількості факторів ризику, що дозволило б уточнити ступінь упевненості в наявності ризику. Для нашого прикладу приймемо Кn = -0,5. Тоді з урахуванням правила нечіткої логіки загальна впевненість у настанні несприятливої події дорівнює К = Ко · К n = 0,38·(-0,5) = - 0,15, де К0 =(К1 v К2 v К3 v К4) = mах (К1 , К2 , К 3 , К 4) = 0,3. Розбіжності результатів, розрахованих першим і другим способами, пояснюється тим, що в другому випадку враховувалася апріорна впевненість у настанні несприятливої події за наявності хоча б одного з факторів ризику (К n = – 0,5), а в першому випадку – ні. Задача 2. (Дерево прийняття рішень). Фірма приймає рішення про будівництво підприємства з можливим розширенням.
· Ймовірність реалізації кожної гілки з випадкової вершини за умов: низького попит у р = 0,25; високого попиту р = 0,75. · Витрати, пов’язані з кожною альтернативою рішень – $ 4,2 млн. за умови можливого розширення через 2 роки. · Статистика попередніх років показує, що доходи за рік роботи за умов різного попиту можуть становити: Доходи за рік роботи
Розв’язання
Рис.6. Дерево рішень для ситуації будівництва 2). У вершині 4 для останніх 8 років “чистий” прибуток становитиме: Е(чистий прибуток /з розширенням) = (0,9·0,75 + 0,2·0,25)·8– 4,2 = 5,8 – 4,2в =1,6 ($млн.); Е(чистий прибуток / без розширення) = (0,25·0,75 + 0,2·0,25) ·8 = 1,9 (млн. $) Висновок: вигідніше у вершині 4 не проводити розширення. 3). У вершині 1 “чистий” прибуток становитиме:: Е (чистий прибуток/велике підприємство)=(1,5·0,75+0,5·0,25)·10 – 5в = 12,5 -5в = 7, 5 (млн. $); Е (чистий прибуток / мале підприємство) = 1,9+ (0,2·0,25+0,25·0,75)·2–1в=1,375 (млн. $) Висновок: оптимальне рішення – будівництво великого підприємства. Задача 3. Проблема 1. Фірма “ ПРОМЕКСПО” отримала пропозицію від закордонних партнерів про поставки до України поліамідних ниток та акрилатних дисперсних систем. При цьму виникає ряд питань: - Чи є ринок збуту цього товару в країні? - Наскільки він є насиченим? - Яка існує конкуренція?
Якісну відповідь на ці питання можуть надати спеціалісти консалтингової фірми, але ціни за їхні послуги є досить високими – $10 000. Проведення ринкових досліджень власними силами потребує певних витрат ($7000), таке дослідження не забезпечить фірму досконалою інформацією, але допоможе прийняти досить коректне рішення. Варіанти отримання прибутку/збитків за сприятливого чи несприятливого ринку наведено в таблиці.
Розв’язання 1). Найкращою комбінацією “ ЕС – рішення” є варіант продажу імпортованих акрилатних дисперсних систем за умови сприятливого ринку з прибутком $50 000 і рішення – нічого не закуповувати за умови несприятливого ринку. Тоді очікуваний прибуток за умов повної визначеності становитиме: 50000 · 0,5 + 0 · 0,5 = $25 000. Тобто за умов повної визначеності – володіння достатньою інформацією можна очікувати на прибуток $25 000 в разі багаторазового повторення рішення.
2) Розраховуємо розмір очікуваної віддачі в грошовому виразі. Крок 1.: якому з трьох варіантів рішення відповідає максимальна грошова віддача. Крок 2. Дерево цілей для даної ситуації наведено на рис. 7 Крок 3. Ймовірності сприятливого та несприятливого ринку акрилатних дисперсних систем оцінюються однаково = 0,5. Як 0,5 оцінюється також імовірність сприятливого і несприятливого ринку поліамідних ниток Крок 4. Оцінити післядію для кожної можливої комбінації альтернатив і станів природи. Закінчене дерево цілей для фірми “ПРОМЕКСПО” показано на рис. 8.
Рис.7. Дерево цілей фірми “ПРОМЕКСПО” Очікувана грошова віддача EMV розраховується зваженням кожної віддачі (післядії) згідно з її ймовірністю та додаванням результатів. При цьому 1 -й стан природи — “сприятливий ринок”, 2 -й — “несприятливий ринок”. Як видно з табл. 8 ймовірність і 1 -го, і 2 -го стану природи оцінюється однаково і становить 0,5. Отже, EMV для альтернативи А1 — імпортувати поліамідні нитки, дорівнює: EMV (A1) = 0,5 ·40 000 + 0,5 · (-20 000) = $10 000. Аналогічно визначаємо EMV для альтернативи А2 — (імпортувати акрилатні дисперсні системи), й A3 — нічого не закуповувати. EMV (A2) = 0,5 · 50 000 + 0,5 · (-20 000) = $15 000; EMV (A3) = 0,5 · 0 + 0,5 ·0 = $ 0.
EVP = Очікувана цінність - max EMV = 25 000 -15 000 = $ 10 000 за умов визначеності. Таким чином, сума, яку фірмі "ПРОМЕКСПО" слід заплатити за досконалу інформацію, не повинна перевищувати $ 10 000. Фірмі "ПРОМЕКСПО", приймаючи рішення про укладання угоди про доцільність закуповування акрилатних дисперсних систем або поліамідних ниток, слід звернутися за досконалою інформацією до консалтингової фірми. При цьому вартість наданої інформації не має перевищувати $ 10 000.
Рис.8. Дерево цілей для фірми “ПРОМЕКСПО” Проблема 2. У керівництва фірми “ПРОМЕКСПО” є альтернатива зверненню до консалтингової фірми – провести маркетингове дослідження власними силами. що потребує витрат у розмірі $ 7000. Шанси, що ринок дійсно виявиться сприятливим в разі, якщо на це вкажуть результати дослідження, оцінюються як 0,45. Імовірність того, що маркетингові дослідження вкажуть на негативний результат – 0,55. Імовірність того, що ринок буде сприятливим, якщо результати дослідження дадуть позитивний результат, – 0,85, а імовірність того, що навіть за умов прийнятних результатів дослідження ринок виявиться несприятливим – 0,15. В разі, якщо результати дослідження виявляться негативними, імовірність сприятливого розвитку ринку складає 0,4, а несприятливого – 0,6. Розв’язання Перша точка рішення – проводити дослідження за $ 7000 чи не проводити. Якщо при цьому приймається рішення не проводити дослідження, тоді альтернатив три: - купувати поліамідні нитки; - купувати акрилатні дисперсні системи; - нічого не закуповувати. Перейдемо до розрахунку очікуваних післядій у грошовому вираженні длякожної гілки. Розпочинаємо з правої частини дерева цілей, ідучи в зворотній бік (“зворотна індукція”): а).Отримані сприятливі результати дослідження: ЕМV (вузол 2)= 0,85 · 33 000 + 0,15 · (-27 000) = $ 24 000; EMV (вузол 3 ) = 0,85 · 43 000 + 0,15 · (-27 000) = $ 32 500. EMV у разі рішення “нічого не закуповувати” становитиме $ -7000. Якщо результат досліджень виявиться сприятливим, слід імпортувати акрилатні дисперсні системи. Очікуване значення післядії (чистий прибуток) = $ 32500 б). Результат дослідження – негативний: ЕМV (вузол 4) = 0,40 · 33 000 + 0,6 · (-27 000) = $ -3000; EMV (вузол 5 ) = 0,40 · 43 000 + 0,6 · (-27 000) = $ 1000. EMV у разі рішення “нічого не закуповувати “становитиме $ -7000. Якщо результат досліджень виявиться негативним, фірмі "ПРОМЕКСПО" слід також імпортувати акрилатні дисперсні системи. Але очікуване значення післядії набагато менше порівняно зі сприятливими результатами дослідження і становить $ 1000. в). Далі, продовжуючи рухатися назад (справа наліво), слід розраховувати очікуване значення післядії при проведенні ринкового дослідження: EMV (вузол 1) = 0,45 · 32 500 + 0,55 · 1000 = $ 15 175. г). Якщо ринкове дослідження не проводилося, EMV становитиме: EMV (вузол 6) = 0,50·40 000 + 0,50 · (-20 000) = $ 10 000.
Дерево цілей фірми “ПРОМЕКСПО” представлено на рис.9. Нижня частина дерева цілей фірми “ПРОМЕКСПО” ідентична дереву цілей на рис.8, а верхня частина ілюструєує рішення доцільності проводення дослідження ринку. Вузол стану природи (проводити дослідження) має дві гілки: результати дослідження позитивні (ймовірність 0,45); результати дослідження негативні (ймовірність 0,55). З усіх верхніх десяти гілок (які передбачають проведення дослідження) віднято вартість ринкових досліджень ($ 7000), при цьому в разі прийняття рішення “нічого не імпортувати” має бути сплачена вартість дослідження – $ 7000 Який можна зробити остаточний висновок?
Рис.9. Дерево прийняття рішень за умов проведення власного дослідження Тема 4: Ризик та елементи теорії корисності Концепція корисності Корисність виражає ступінь задоволення, яку одержує суб’єкт від споживання товару або виконання певних дій. В економічному аналізі це поняття використовується для опису пріоритетності при розрахунках: · рішення х байдуже (еквівалентне) до рішення у: х ~ у, тобто немає різниці, кому надавати перевагу; · рішення х пріоритетніше за рішення у: x Якщо існує неперервна дійсна функція U = f(x), тоця функція називається функцією корисності, якщо U(x) > U(y) при x Поняття лотереї Простою лотереєю L (х1, р, х2) називається імовірнісна подія, що має два можливих результати х1 і х2, імовірності настання яких позначимо відповідно через р і (1 - р). Наприклад, якщо х1 ~ L (х2, р, х3), то це означає, що результат х1 рівноцінний лотереї, що має наслідки х2 з імовірністю р або х3 з імовірністю (1 - р). Якщо хо Сподівана корисність Лотерея L може привести до різних виграшів, які задані рядом розподілу:
Сподіваний виграш у лотереї дорівнюватиме математичному сподіванню випадкової величини - величини виграшу: Основна формула теорії корисності дозволяє розрахувати корисність ансамблю результатів лотереї за умов відомої функції корисності U(x): Якщо можливий розподіл ймовірностей виграшів задається неперервною щільністю розподілу f(x), то сподіваний виграш знаходитиметься за формулою
Детермінований еквівалент лотереї - це гарантована сума Тоді страховою сумою буде величина, протилежна до детермінованого еквівалента лотереї. Премія за ризик r(х) – це сума, якою особа, що приймає рішення може знехтувати (r(х) < Mx), щоб уникнути ризику, пов’язаного з лотереєю, тобто лотерея є більш несприятливою ситуацією, ніж та, в якій перебуваєособа: r(х) = Mx - Розв’язання 1. Для першого рішення Корисність рішення
2. Для другого рішення Корисність
3.Для третього рішення Корисність Висновок: за умови однакової сподіваної зарплати третє рішення має більшу корисність.
Задача 2. Особа з доходом 1,5 тис.гр.од. оцінює можливість перейти на нове місце роботи, повязанез певним ризиком: дохід на новому місці може бути вдвічі більшим або знизитися до 1тис.гр.од. із імовірністю 0,5. СПР має таку шкалу корисності:
Який варіант слід обрати? Розв’язання 1). Побудуємо графік інтервально- нейтральної функції корисності і запишемо її аналітичний вигляд:
U(x) = 6x+ 4, x 2x + 12, x
2). Дохід на старому місці роботи 1,5 тис.гр.од має корисність: U(x)= 6x+ 4 = 6 ·1,5 =13. Рівень корисності для нового місця роботи становитиме:
Висновок: нове місце роботи матиме вищий рівень користності.
3). Детермінований еквівалент лотереї:
4). Сподіваний дохід на новому місці складатиме: Премія за ризик: Ця величина показує суму, якою особа може знехтувати, вибираючи стабільний дохід у 1,5 тис.гр.од порівняноіз роботою з більшим сподіваним доходом у 2 (тис.гр.од) і з суттєвим ризиком. Основні поняття теорії ігор Прийняття маркетингових рішень найчастіше пов’язане з ситуаціями, в яких перетинаються інтереси двох (або більше) конкуруючих сторін, які мають різні цілі. Такі ситуації називають конфліктними. Математичною теорією конфліктних ситуацій є теорія ігор. Розв’язанню задач такого типу передує: визначення правил гри, можливої кількості гравців, можливих виграшів. Грою називається спрощена формалізована модель реальної конфліктної ситуації з сукупністю правил, які регламентують поведінку гравців. Хід у грі – це вибір гравцем одного з можливих варіантів дій. Наслідком є рішення гравця під час ходу, значення певної функції виграшу. Стратегія або дія, до якої вдається гравець, залежить від ситуації. За умов застосування гравцями в процесі гри різних стратегій матимемо гру в мішаних стратегіях, а елементи стратегій називають чистими стратегіями. Одним з основних видів ігор є матричні ігри – парні ігри з нульовою сумою: виграш одного гравця дорівнює програшу іншого за умови обмеженої кількості стратегій кожного гравця, а спільна сума виграшів дорівнює нулю, наприклад, ігри з природою, коли гравцями є фірма і природа. Платіжною матрицею гри є прямокутна матриця, елементами якої є числа aij, які характеризують виграш – наслідок вибору гравцем А стратегії Aі, а гравцем В – стратегії Bj.
Розв’язати гру означає знайти оптимальну стратегію для кожного гравця, яка за умов багаторазового повторення гри забезпечує максимально можливий середній виграш (мінімально можливий середній програш). Критерієм вибору раціональних рішень є критерії мінімакса або максиміна: · для гравця А оптимальною є стратегія максимізації мінімального виграшу за всіма можливими стратегіями гравця В: А опт : · для гравця В оптимальною є стратегія мінімізації максимального програшу за всіма можливими стратегіями гравця А: В опт : де α – мінімально можливий виграш гравця А – нижня ціна гри; β – максимально можливий програш гравця В – верхня ціна гри. Оптимального розв ’ язку гра досягає за умови, що кожній стороні невигідно змінювати свою стратегію, бо протилежна сторона може теж обрати іншу стратегію, яка погіршить виграш першого гравця. Якщо α = β, то гра має сідлову точку, а значення ν = α = β є ціною гри. При цьому сторони обирають чисті стратегії: максимінна для гравця А і мінімаксна для гравця В. Якщо α ≠ β, то ціна гри дорівнює математичному сподіванню виграшу першого гравця за умов вибору гравцями оптимальних стратегій: V = M (S*; Θ*), де S*; Θ * – оптимальні стратегії першого і другого гравця, і M (S; Θ *) ≤ V ≤ M (S*; Θ), де M (S; Θ) – математичне сподівання середнього виграшу першого гравця за умов вибору гравцями стратегій S та Θ. В цьому випадку гра не має сідлової точки, чисті стратегії – неоптимальні: можна покращити стан кожного гравця, обравши мішані стратегії – певні комбінації початкових чистих стратегій з певними частотами (ймовірностями) вибору кожної з них: для гравця А: P = (p1, p2,…, pm), для гравця B: Q = (q1, q2,…, qn), Оптимальні значення §2. Графічний спосіб розв`язання гри 1). Звести гру (m х n) до (m х 2) або (2 х n) відкиданням невигідних стратегій для кожного гравця.
2). Очікувані виграші гравця А будуть лінійно залежними від частоти вибору ним першої стратегії (р1) для всіх варіантів чистих стратегій В:
3). На горизонтальній осі р відкласти відрізок [0;1], через кінці якого провести вертикальні лінії – лінії стратегій А1 і А2. В обраному масштабі побудувати лінії очікуваних виграшів гравця А для різних можливих стратегій Вк, гравця В за правилом: . a1n·p1 + a2n·p2., к = 1,2,..., п.
Нижню межу виграшу, який може отримати гравець А, визначити з положення ламаної лінії, на якій вибирається найвища точка (в ній перетинаються певні прямі – лінії стратегій Вп). Координати цієї точки знаходяться як розв’язки системи лінійних рівнянь, що характеризують відповідні прямі. Крім того, слід пам’ятати, що Практикум: Елементи теорії ігор Задача 1. Розв’язати гру, задану платіжною матрицею
1). Стратегія А3 є невигідною для гравця А: А1, А2 >А3, а стратегії В3,В4 є невигідними для гравця В: В3, В4 >В5, тому складаємо нову платіжну матрицю гри:
2). Визначаємо ціну гри: α = тіп (тах aij) = min {6;5;5;4} = 4; β = max(min aij) =max{1;2}= 2; α ≠ β, тому α ≤ ν ≤ β, тобто 2 ≤ ν ≤ 4. 3). Будуємо лінії очікуваних виграшів для гравця А на рис. 12:
|
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.43 (0.028 с.) |






























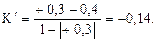
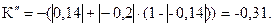






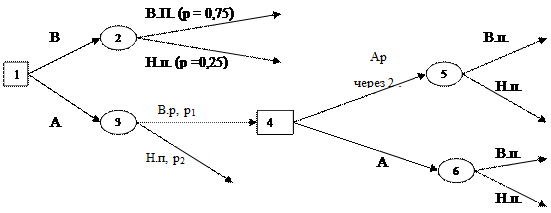 1). Будуємо дерево рішень – рис.6:
1). Будуємо дерево рішень – рис.6:
 Крок 5. Максимальний EMV – y варіанті А2. Отже, слід закуповувати партію акрилатних дисперсних систем. Тепер ми маємо необхідні дані для визначення очікуваної цінності досконалої інформації EVP:
Крок 5. Максимальний EMV – y варіанті А2. Отже, слід закуповувати партію акрилатних дисперсних систем. Тепер ми маємо необхідні дані для визначення очікуваної цінності досконалої інформації EVP: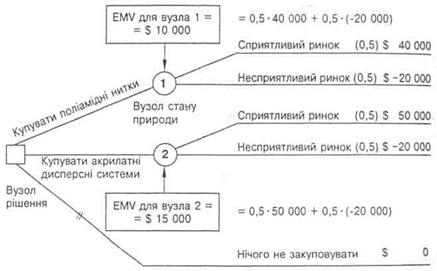

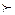 y, якщо х не гірше за у, а у гірше за х.
y, якщо х не гірше за у, а у гірше за х. х
х 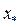 - найменш пріоритетне рішення, х* - найбільш пріоритетне рішення, то можна порівняти значення функцій корисності
- найменш пріоритетне рішення, х* - найбільш пріоритетне рішення, то можна порівняти значення функцій корисності  . Тоді лотереєю L(хо; р(х); х*) називається ситуація, в якій найменш пріоритетне рішення хо отримується з ймовірністю p(x), a найбільш пріоритетне рішення х* отримується з ймовірністю q(x) = 1 - p(x). Для такої лотереї корисність за Нeйманом визначатиметься функцією U (x)= p(x), коли особі байдуже або принаймні участь в лотереї L(хо; р(х); х*), або отримувати гарантоване значення суми х.
. Тоді лотереєю L(хо; р(х); х*) називається ситуація, в якій найменш пріоритетне рішення хо отримується з ймовірністю p(x), a найбільш пріоритетне рішення х* отримується з ймовірністю q(x) = 1 - p(x). Для такої лотереї корисність за Нeйманом визначатиметься функцією U (x)= p(x), коли особі байдуже або принаймні участь в лотереї L(хо; р(х); х*), або отримувати гарантоване значення суми х.


 , а корисність ансамблю результатів лотереї при цьому можна розрахувати відповідно таким чином:
, а корисність ансамблю результатів лотереї при цьому можна розрахувати відповідно таким чином:
 , отримання якої еквівалентне участі в лотереї:
, отримання якої еквівалентне участі в лотереї:  ~ L і визначається зрівняння:
~ L і визначається зрівняння: 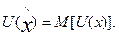
 .
. (ум. гр.од.) – сподівана зарплата
(ум. гр.од.) – сподівана зарплата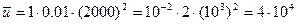 .
. (ум. гр.од.).
(ум. гр.од.).
 (ум,гр.,од.).
(ум,гр.,од.).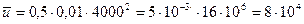 .
.
 10 x, x
10 x, x 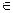 [ 0;1 ];
[ 0;1 ];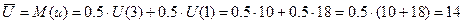 .
.
 ,
, 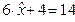
 =1,6
=1,6 (тис.гр.од).
(тис.гр.од). (тис.гр.од).
(тис.гр.од).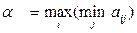 ;
;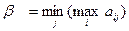 ,
,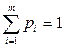 ;
; .
. визначають умову існування очікуваного оптимального значення ціни гри
визначають умову існування очікуваного оптимального значення ціни гри  .
.



