
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схильність – несхильність до ризикуСодержание книги
Поиск на нашем сайте
Особа є несхильною до ризику, якщо можливість одержання детермінованого еквівалента лотереї є для неї пріоритетнішою за участь в лотереї. При цьому:
Рис.16. Графік функції корисності особи, несхильної до ризику. Особа є схильною до ризику, якщо для неї пріоритетнішою є участь в лотереї за можливість одержання детермінованого еквівалента лотереї. При цьому:
Рис. 17. Графік функції корисності особи, схильної до ризику. Нейтральність до ризику проявляється в байдужому ставленні до отримання детермінованого еквівалента лотереї чи участі в лотереї. При цьому:
Існує гіпотеза: схильність до ризику проявляється в разі наявності невеликих грошових сум відносно загального достатку, а несхильність – для існування значних сум. Несхильність до ризику – основа діяльності страхових компаній. Схильність до ризику – основа грального бізнесу.
Рис. 18. Графік функції схильномті – несхильності до ризику.
Якщо функція схильності - несхильності до ризикує функцією розподілу ймовірностей F(x) i функція щільності розподілу ймовірностей f(x)=F'(x), то матимемо лотерею із неперервним розподілом ймовірностей: L (x є [x*; x*]; f(x)). Тоді ставлення до ризику – локальну характеристику особи аналітично можна задати «зрізаною» функцією розподілу ймовірностей:
де х*, а*, b* є нормалізованими значеннями параметрів х, а. b, а Ф(х) – функція Лапласа для нормального розподілу N(m;σ).
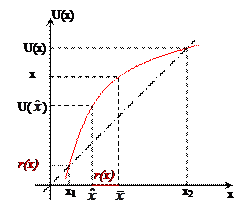
Приклад. Побудувати інтервально-нейтральну функцію корисності, задану шкалою:
Для двох точок з відомими координатами A (xА, UА), B (xB, UB) запишемо рівняння прямої, яка проходить через дві точки:
Виходячи з цього, отримуємо рівняння інтервально- нейтральної функції корисності
0,015x – 0,1, x U(x) = 0,020x – 0,2, x 0,025x – 0,35, x 0,035x – 0,75, x
U(х)
Рис.19. Графік інтервально- нейтральної функції корисності х Стратегічною еквівалентністю вважатимемо існування такої пари фукцій корсності U1 (x) ~ U2 (x), якщо вони однаково впорядковують за ступенем привабливості довільну пару лотерей:
U1 (x) ~ U2 (x) => U1 (x) = a + b ∙U2 (x). U1 (x) = a + b ∙ x ~ U2 (x) = х U1 (x) = a − b ∙е−сх ~ U2 (x) = − е−сх
Практикум: Ризик із урахуванням корисності Задача 1. Особа з функцію корисності U(x)=0.01·x2, має альтернативні варіанти вибору місця роботи: 1 – стабільна зарплата 2000 ум. гр.од. 2 – з ймовірністю 0,5 можна отримувати зарплату 1000 і 3000 ум. гр.од. 3 – 4000 ум.гр. одиниць або не отримати нічого з ймовірністю 0,5 Яке рішення слід обрати? Розв’язання 1. Для першого рішення Корисність рішення
2. Для другого рішення Корисність
3.Для третього рішення Корисність Висновок: за умови однакової сподіваної зарплати третє рішення має більшу корисність.
Задача 2. Особа з доходом 1,5 тис.гр.од. оцінює можливість перейти на нове місце роботи, повязанез певним ризиком: дохід на новому місці може бути вдвічі більшим або знизитися до 1тис.гр.од. із імовірністю 0,5. СПР має таку шкалу корисності:
Який варіант слід обрати? Розв’язання 1). Побудуємо графік інтервально- нейтральної функції корисності і запишемо її аналітичний вигляд:
U(x) = 6x+ 4, x 2x + 12, x
2). Дохід на старому місці роботи 1,5 тис.гр.од має корисність: U(x)= 6x+ 4 = 6 ·1,5 =13. Рівень корисності для нового місця роботи становитиме:
Висновок: нове місце роботи матиме вищий рівень користності.
3). Детермінований еквівалент лотереї:
4). Сподіваний дохід на новому місці складатиме: Премія за ризик: Ця величина показує суму, якою особа може знехтувати, вибираючи стабільний дохід у 1,5 тис.гр.од порівняноіз роботою з більшим сподіваним доходом у 2 (тис.гр.од) і з суттєвим ризиком. Тема 3: ТЕОРЕТИКО – ІГРОВА МОДЕЛЬ РИЗИКУ
3.1. Елементи теорії ігор Основні поняття теорії ігор Прийняття маркетингових рішень найчастіше пов’язане з ситуаціями, в яких перетинаються інтереси двох (або більше) конкуруючих сторін, які мають різні цілі. Такі ситуації називають конфліктними. Математичною теорією конфліктних ситуацій є теорія ігор. Розв’язанню задач такого типу передує: визначення правил гри, можливої кількості гравців, можливих виграшів. Грою називається спрощена формалізована модель реальної конфліктної ситуації з сукупністю правил, які регламентують поведінку гравців. Хід у грі – це вибір гравцем одного з можливих варіантів дій. Наслідком є рішення гравця під час ходу, значення певної функції виграшу. Стратегія або дія, до якої вдається гравець, залежить від ситуації. За умов застосування гравцями в процесі гри різних стратегій матимемо гру в мішаних стратегіях, а елементи стратегій називають чистими стратегіями. Одним з основних видів ігор є матричні ігри – парні ігри з нульовою сумою: виграш одного гравця дорівнює програшу іншого за умови обмеженої кількості стратегій кожного гравця, а спільна сума виграшів дорівнює нулю, наприклад, ігри з природою, коли гравцями є фірма і природа. Платіжною матрицею гри є прямокутна матриця, елементами якої є числа aij, які характеризують виграш – наслідок вибору гравцем А стратегії Aі, а гравцем В – стратегії Bj.
Розв’язати гру означає знайти оптимальну стратегію для кожного гравця, яка за умов багаторазового повторення гри забезпечує максимально можливий середній виграш (мінімально можливий середній програш). Критерієм вибору раціональних рішень є критерії мінімакса або максиміна: · для гравця А оптимальною є стратегія максимізації мінімального виграшу за всіма можливими стратегіями гравця В: А опт : · для гравця В оптимальною є стратегія мінімізації максимального програшу за всіма можливими стратегіями гравця А: В опт : де α – мінімально можливий виграш гравця А – нижня ціна гри; β – максимально можливий програш гравця В – верхня ціна гри. Оптимального розв ’ язку гра досягає за умови, що кожній стороні невигідно змінювати свою стратегію, бо протилежна сторона може теж обрати іншу стратегію, яка погіршить виграш першого гравця. Якщо α = β, то гра має сідлову точку, а значення ν = α = β є ціною гри. При цьому сторони обирають чисті стратегії: максимінна для гравця А і мінімаксна для гравця В. Якщо α ≠ β, то ціна гри дорівнює математичному сподіванню виграшу першого гравця за умов вибору гравцями оптимальних стратегій: V = M (S*; Θ*), де S*; Θ * – оптимальні стратегії першого і другого гравця, і M (S; Θ *) ≤ V ≤ M (S*; Θ), де M (S; Θ) – математичне сподівання середнього виграшу першого гравця за умов вибору гравцями стратегій S та Θ. В цьому випадку гра не має сідлової точки, чисті стратегії – неоптимальні: можна покращити стан кожного гравця, обравши мішані стратегії – певні комбінації початкових чистих стратегій з певними частотами (ймовірностями) вибору кожної з них: для гравця А: P = (p1, p2,…, pm), для гравця B: Q = (q1, q2,…, qn), Оптимальні значення §2. Графічний спосіб розв`язання гри 1). Звести гру (m х n) до (m х 2) або (2 х n) відкиданням невигідних стратегій для кожного гравця.
2). Очікувані виграші гравця А будуть лінійно залежними від частоти вибору ним першої стратегії (р1) для всіх варіантів чистих стратегій В:
3). На горизонтальній осі р відкласти відрізок [0;1], через кінці якого провести вертикальні лінії – лінії стратегій А1 і А2. В обраному масштабі побудувати лінії очікуваних виграшів гравця А для різних можливих стратегій Вк, гравця В за правилом: . a1n·p1 + a2n·p2., к = 1,2,..., п.
Нижню межу виграшу, який може отримати гравець А, визначити з положення ламаної лінії, на якій вибирається найвища точка (в ній перетинаються певні прямі – лінії стратегій Вп). Координати цієї точки знаходяться як розв’язки системи лінійних рівнянь, що характеризують відповідні прямі. Крім того, слід пам’ятати, що Практикум: Елементи теорії ігор Задача 1. Розв’язати гру, задану платіжною матрицею
1). Стратегія А3 є невигідною для гравця А: А1, А2 >А3, а стратегії В3,В4 є невигідними для гравця В: В3, В4 >В5, тому складаємо нову платіжну матрицю гри:
2). Визначаємо ціну гри: α = тіп (тах aij) = min {6;5;5;4} = 4; β = max(min aij) =max{1;2}= 2; α ≠ β, тому α ≤ ν ≤ β, тобто 2 ≤ ν ≤ 4. 3). Будуємо лінії очікуваних виграшів для гравця А на рис. 12:
4·р1 + 2· р2 = ν, р2 = 1- р1. р1 + р2 = 1. Звідки отримуємо розв’язки системи – оптимальні значення частот (імовірностей) вибору стратегій А1, А2 для гравця А:
Рис.12. Лінії виграшів гри 5). Для визначення оптимальних стратегій гравця В, які він може застосовувати з частотами
Аналогічно до попереднього знаходимо: Висновок: Для максимізації мінімального виграшу гравцеві А доцільно застосовувати стратегії А1, А2 з частотами
Задача 2. Визначити оптимальну стратегію підприємства, яка забезпечуватиме певний середній дохід від реалізації товару за будь-якої погоди: середній очікуваний прибуток і розмір оптимальної партії товару. Дані про придбання товару й умови реалізації наведено в таблиці
Розв’язання 1). Маємо гру з природою: фірма – погода. Фірма має 2 чисті стратегії: стратегія А – реалізація товару з розрахунком на теплу погоду; стратегія В – реалізація товару з розрахунком на прохолодну погоду. Природа, як другий гравець, теж має 2 чисті стратегії: стратегія С – тепла погода; стратегія D – прохолодна погода.
2). Розрахуємо таблицю 6 – таблицю стратегій фірми і погоди:
3).Розраховуємо платіжну матрицю гри: · За умови вибору стратегії А у випадку теплої погоди дохід складатиме: (А; С) → 1950·(16 - 8) + 600· (48 – 27) = 28200 (ум. гр.од.). · За умови вибору стратегії А у випадку прохолодної погоди дохід буде меншим за рахунок втрат від нереалізованої продукції – суконь: (А; D) → 625·(16 - 8) + 600· (48 – 27) - (1950 – 625) · 8 = 7000 (ум гр.од.). · За умови вибору стратегії В у випадку прохолодної погоди дохід складатиме (В; D) → 625·(16 - 8) + 10000· (48 – 27) = 26000 (ум. гр.од.). · За умови вибору стратегії В у випадку теплої погоди дохід буде меншим за рахунок втрат від нереалізованої продукції – костюмів: (В;С) → 625·(16 - 8) + 600· (48 – 27) - (1000 – 600) · 27 = 6800 (ум. гр.од.).
Таким чином, платіжна матриця грн має вигляд:
Перший гравець (фірма) не отримає прибутку менше за 6800 ум. гр..од., а за умов співпадання погодних умов з обраною стратегією виграш – дохід складатиме 27800 ум. гр.од. або 26000 ум. гр.од. Ціна гри при цьому –середній очікуваний прибуток знаходитиметься в межах [7000; 26000].
4). За умов невизначеності майбутніх погодних умов найбільш гарантований дохід фірмі забезпечує комбіноване застосування стратегій А та В, тобто мішану стратегію гри, а середній дохід складається з урахуванням відносної частоти застосування стратегій: стратегії А з імовірністю р, стратегії В з імовірністю (1- р).
Тоді дохід для теплої погоди становитиме: 28200 · p + 6800 · (1- p); дохід для прохолодної погоди: 7000 · p + 26000 · (1- p). 28200 · p + 6800 · (1- p) = 7000 · p + 26000 · (1- p). 40000 · р = 19200, р = 19200/40400 ≈ 0,48. Перший гравець (фірма), застосовуючи стратегії А та В у відношенні 48: 100, матиме мішану стратегію, яка забезпечить у будь-якому випадку середній дохід в розмірі:
28200 · 0,48 + 6800 · 0,52 = 13344 + 3536 = 168000 (ум. гр..од.). При цьому можна обчислити розмір оптимальної партії товару: (1950 с. + 600 к.) · 0,48 + (625 с.. + 1000 к.) · 0,52 = 1261 с.. + 808 к.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.74.187 (0.011 с.) |

 ;
;
 ;
;
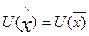 ;
; Функція схильності-несхильності до ризику є певною комбінацією локальних функцій корисності (рис.18).
Функція схильності-несхильності до ризику є певною комбінацією локальних функцій корисності (рис.18). або
або 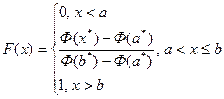 ,
, .
. 0,005x, x
0,005x, x 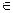 [ 0;10 ];
[ 0;10 ];
 a, b:
a, b: (ум. гр.од.) – сподівана зарплата
(ум. гр.од.) – сподівана зарплата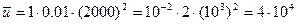 .
. (ум. гр.од.).
(ум. гр.од.).
 (ум,гр.,од.).
(ум,гр.,од.).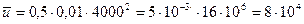 .
.
 10 x, x
10 x, x 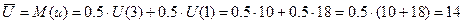 .
.
 ,
, 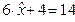
 =1,6
=1,6 (тис.гр.од).
(тис.гр.од). (тис.гр.од).
(тис.гр.од).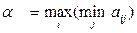 ;
;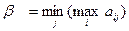 ,
,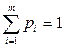 ;
; .
. визначають умову існування очікуваного оптимального значення ціни гри
визначають умову існування очікуваного оптимального значення ціни гри  .
.
 4). Нижньою межею виграшу є ламана МNK на рис.12, у верхній точці якої – точці N виграш досягає максимуму. Ця точка є точкою перетину прямих В5 і В6, тому маємо таку систему рівнянь:
4). Нижньою межею виграшу є ламана МNK на рис.12, у верхній точці якої – точці N виграш досягає максимуму. Ця точка є точкою перетину прямих В5 і В6, тому маємо таку систему рівнянь: 1·р1 + 5· р2 = ν, 1·р1 + 5· р2 = 4·р1 + 2· р2,
1·р1 + 5· р2 = ν, 1·р1 + 5· р2 = 4·р1 + 2· р2,  . Ціна гри ν* = 1·
. Ціна гри ν* = 1· 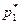 + 5
+ 5 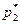 = 3.
= 3.
 , аналізуємо рис.12: через точку N проходять прямі стратегій В5 і В6 , а застосування стратегій В1 і В2 призводить до програшу більших сум, тому
, аналізуємо рис.12: через точку N проходять прямі стратегій В5 і В6 , а застосування стратегій В1 і В2 призводить до програшу більших сум, тому 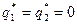
 ,
, 






