
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра железобетонных и каменных конструкцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кафедра железобетонных и каменных конструкций А.А. ВЕСЕЛОВ А.В. СКОННИКОВ В.И. ЖУКОВ ЖЕЛЕЗОБЕТОННЫЕ КОНСТРУКЦИИ Санкт-Петербург УДК 624.012.45
Железобетонные конструкции: Учеб.пособие / А. А. Веселов, А. В. Сконников, В. И. Жуков; СПб гос. арх.-стр. ун-т. СПб., 2007. 88 с. ISBN 5-230-09462-4
В пособие даются пояснения по выбору расчетных схем, сбору нагрузок и предлагается методика расчета. Расчеты сопровождаются ссылками на литературные и нормативные источники, а также учитываются рекомендации по конструированию железобетонных конструкций. Выполнение курсового проекта № 1 по железобетонным конструкциям рассчитано на использование данного учебного пособия и ранее изданных методических указаний, в которых приведены задание на курсовое проектирование в соответствии с шифром (номер зачетной книжки) студента, состав и объем проекта № 1 и необходимые справочные материалы, а также нормативных документов. Пособие рассчитано на студентов всех строительных специальностей заочной и вечерней форм обучения и может быть использовано студентами дневной формы обучения.
Р е ц е з е н т ы: М. П. Ерохин, Ю. С. Конев (СПбГАСУ) ISBN 5-230-09462-4 © Санкт-Петербургский архитектурно-строительный университет
ВВЕДЕНИЕ Курсовое проектирование призвано закрепить теоретические знания, привить необходимые навыки практического их применения, стимулировать профессиональную подготовку будущих специалистов. В процессе курсового проектирования студенты знакомятся с нормативными документами по расчету и конструированию элементов зданий и сооружений, осваивают методику инженерных расчетов, степень их детализации и получают опыт графического оформления проекта. При выполнении курсового проекта № 1 по железобетонным конструкциям, кроме данного учебного пособия, рекомендуем использовать методические указания [9, 10] по курсовому проектированию, разработанные на основе СНиП 2.03.01 – 84. В работах [9, 10] приведены задания на курсовое проектирование в соответствии с шифром (номером зачетной книжки), определены состав и объем расчетной и графической частей курсового проекта, даны ссылки на литературные источники. Курсовой проект № 1 по железобетонным конструкциям предусматривает проектирование междуэтажных перекрытий четырехэтажного промышленного здания с несущими кирпичными стенами и внутренним неполным железобетонным каркасом, а также колонн и фундаментом под них.
Междуэтажные перекрытия проектируются в двух вариантах – в монолитном и сборном железобетоне, при этом для монолитного перекрытия производятся расчет и конструирование только плиты и второстепенной балки. Перекрытия в сборном железобетоне проектируются полностью – с расчетом и конструированием плиты, неразрезного ригеля, колонны с консолями и фундамента. В задании на курсовое проектирование приводятся схематические план и разрез здания, указывается длина и ширина здания в свету, между внутренними гранями стен; высота этажей между отметками чистого пола; временная нагрузка на перекрытия, в том числе кратковременная; снеговая нагрузка; расчетное давление на основание и другие сведения; привязка стен к разбивочным осям равна 120 мм. Студенты специальности 2903 ПГС выполняют проект в полном объеме. Студенты других специальностей разрабатывают проект только сборного перекрытия, при этом им разрешается проектировать ригель разного типа и не рассчитывать прогиб панели. Курсовой проект № 1 представляется в виде расчетно-пояснительной записки, четко написанной ручкой без помарок на стандартных листах с полями. В записке должны быть приведены расчетные схемы и эскизы, поясняющие текст. Графическая часть проекта выполняется на 1,5 – 2,0 стандартных листах чертежей со спецификацией арматуры и выборкой материалов (пример оформления – см. приложение). Фактический объем курсового проекта устанавливается преподавателем на практических занятиях или на вводных лекциях.
Единицы СИ в расчетах железобетонных конструкций. За единую систему физических величин принята СИ – единичная Международная система единиц. Перечень единиц физических величин, подлежащих применению в строительстве, был введен в действие с 1 июля 1984 г. [14]. Так как 1 МПа (мегапаскаль) соответствует 1Н/мм2 (Н – ньютон), в учебном пособии в расчетах элементов введены: сила и нагрузка, Н (ньютон), размеры сечений, мм, соответственно площади сечений – мм2, объемы, статические моменты сопротивления сечений – мм3, моменты инерции сечения – мм4; напряжения, расчетные сопротивления, модуль упругости и сдвига – Н/мм2, или что то же, МПа.
I. ПРОЕКТИРОВАНИЕ МОНОЛИТНОГО ЖЕЛЕЗОБЕТОННОГО ПЕРЕКРЫТИЯ
В соответствии с заданием требуется запроектировать четырехэтажное здание промышленного типа с размерами в плане между внутренними гранями стен L = 36,6 м, В = 24,6 м. Стены кирпичные несущие толщиной 510 мм. Привязка разбивочных осей стен принята равной 120 мм. Оконные проемы в здании приняты шириной 2,3 м, высотой 2,1 м. Высота этажей между отметками чистого пола h эт = 4,2 м. Временная нагрузка нормативная на всех междуэтажных перекрытиях vn = 12 кН/м2, в том числе кратковременная vshn = 1,5 кН/м2. Снеговая нагрузка на кровле v сн n = 1 кН/м2. Подошва фундаментов основывается на грунте с расчетным сопротивлением R = 0,3 МПа. Отметка подошвы фундамента – 1,5 м. Междуэтажные железобетонные перекрытия опираются на наружные кирпичные стены и внутренние железобетонные колонны. Кровельное покрытие опирается только на наружные стены. В качестве несущих элементов покрытия используются сборные железобетонные фермы или балки. Промежуточные колонны доводятся только до междуэтажного перекрытия четвертого этажа. Классы бетона и арматуры выбираются проектировщиками в соответствии с действующими нормативными документами. Состав пола на междуэтажных перекрытиях и на первом этаже принимается типовым в зависимости от назначения помещения и характера технологии производства в нем.
Разбивка балочной клетки
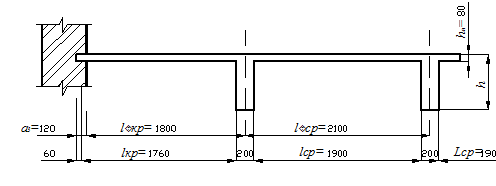
Основные принципы проектирования разбивочной схемы балочной клетки монолитного железобетонного перекрытия изложены в учебнике [7] и учебном пособии [10]. При рекомендуемой величине пролетов второстепенных и главных балок от 5,0 до 7,0 м, в зависимости от интенсивности временной нагрузки на заданной длине здания в свету L = 36,6 м и ширине В = 24,6 м могут быть приняты 6 пролетов второстепенных продольных балок и 4 пролета главных поперечных балок. С учетом рекомендаций [10] о целесообразности уменьшения до 10 % крайних пролетов балок в сравнении со средним получим (рис. 1)
L = 36,6 м = 0,9 l 1 + 4 l 1 + 0,9 l 1 = 5,8 l 1,
откуда l 1 = 36,6: 5,8 = 6,31 м.
Принимая с округлением средние пролеты второстепенных балок l ср = 6,3 м, получим величину крайних пролетов
l кр = (36,6 – 6,3 × 4): 2 = 5,7 м.
При рекомендуемом шаге второстепенных балок от 1,8 до 2,5 м в каждом из четырех пролетов главных балок могут расположиться по три пролета плиты. С учетом рекомендаций [10] о целесообразности уменьшения до 20 % крайних пролетов плиты в сравнении со средними получим В = 24,6 м = 0,8 l 2 + 10 l 2 + 0,8 l 2 = 11,6 l 2, откуда l 2 = 24,6: 11,6 = 2,12 м.
Рис. 1.
Принимая с округлением средние пролеты плиты l¢ ср = 2,1 м, получим величину крайних пролетов
l¢ кр = (24,6 – 2,1 × 10): 2 = 1,8 м.
Расчет плиты перекрытия В соответствии с п. 5.4 [2] толщина плиты монолитных перекрытий промышленных зданий принимается не менее 60 мм. Принимаем толщину плиты hf = 80 мм (уточнение см. на с. 14). Для определения расчетных пролетов плиты задаемся приближенно размерами поперечного сечения второстепенных балок: h = l: 12 = 6300: 12 = 525 мм; b = h: 3 = 525: 3 = 175 мм и принимаем h = 550 мм; b = 200 мм(уточнение см. на с.18). За расчетные пролеты плиты принимаем: в средних пролетах – расстояния в свету между гранями второстепенных балок, а в крайних – расстояния от граней второстепенных балок до середины площадок опирания плиты на стену (рис. 2).
Рис. 2
При ширине второстепенных балок b = 200 мм и глубине заделки плиты в стену в рабочем направлении а 3 = 120 мм (полкирпича) получим
l кр = l ¢¢кр – 0,5 b + 0,5 а 3 = 1800 – 0,5 × 200 + 0,5 × 120 = 1760 мм; l ср = l ¢ср – 2 × 0,5 b = 2100 – 2 × 0,5 × 200 = 1900 мм.
Расчетные пролеты плиты в длинном направлении при ширине главных балок (ориентировочно) 300 мм и глубине заделки плиты в стены в нерабочем направлении а 3 = 60 мм (четверть кирпича)
l кр1 = 5700 – 0,5 × 300 + 0,5 × 60 = 5580 мм; l ср = 6300 – 2 × 0,5 × 300 = 6000 мм.
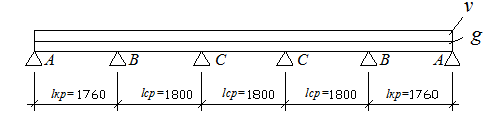
При соотношении длинной и короткой сторон 5580: 1900 = = 2,94 @ 3,0 плита условно рассчитывается [4] как балочная неразрезная многопролетная, работающая в коротком направлении по схеме рис. 3.
Рис. 3
Расчетные нагрузки на условную полосу плиты шириной 1,0 м, кН/м: а) постоянная вес пола из цементного раствора с затиркой при толщине слоя 2,0 см и плотности 1700 кг/м3
1700 × 0,02 × 1,0 × 1,3 × 10 –2 = 0,44;
вес плиты толщиной 80 мм при плотности 2500 кг/м3
2500 × 0,08 × 1,0 × 1,1 × 10-2 = 2,2;
полная постоянная нагрузка
g = 0,44 + 2,2 = 2,64;
б) временная при vn = 12 кН/м2
v = 12 × 1,0 × 1,2 = 14,4.
Здесь 1,3; 1,1 и 1,2 – коэффициенты надежности по нагрузке [15]. Полная расчетная нагрузка
g + v = 2,64 + 14,4 = 17,04 кН/м.
Постоянная и длительная
17,04 – 1,5.1.2 =15.24 кН/м.
Величины расчетных изгибающих моментов в неразрезной балочной плите с равными или отличающимися не более чем на 20 % пролетами (l ср: l кр= 1900: 1760 = 1,08 < 1,2) определяются с учетом перераспределения усилий вследствие пластических деформаций бетона и арматуры в соответствии с [4] по формулам: В крайних пролетах
М кр =
в средних пролетах и над средними опорами (см. рис. 2, 3)
М ср = – Мс = ±
над второй от конца опорой при армировании рулонными сетками (непрерывное армирование)
МВ = -
то же при армировании плоскими сетками (раздельное армирование)
МВ = -
где l – больший из примыкающих к опоре расчетный пролет. Определение толщины плиты. Для монолитного железобетонного перекрытия принимаем бетон проектного класса по прочности на сжатие В 15. С учетом соотношения длительных нагрузок к полным равного 15,24 / 17,04 = 0,89 < 0,9 (в соответствии с п. 3.3 [2]) расчетные сопротивления определяются с коэффициентом условий работы g b 1 = 1; Rb = 1 × 8,5 = 8,5 МПа; Еb = 24000 МПа; Rbt = 1 × 0,75 = = 0,75 Мпа.
Арматуру в плите перекрытия принимаем для двух вариантов армирования: арматурой класса В500 с расчетным сопротивлением Rs = = 415 МПа = 415 Н/мм2 при армировании рулонными сварными сетками (непрерывное армирование), Еs = 200000 МПа; арматурой класса А400 с расчетным сопротивлением Rs = = 355 МПа = 355 Н/мм2 при армировании плоскими сетками (раздельное армирование), Еs = 200000 МПа. Необходимую толщину плиты перекрытия определяем при среднем оптимальном коэффициенте армирования m = 0,006 по максимальному моменту МВ = 5,6 кНм и ширине плиты b'f = 1000 мм. Расчетная высота сечения плиты при относительной ее высоте x = Таблица 1
Продолжение таблицы 1
при αm = x (1 – 0,5x) и Мmax = 5,32 кНм
αm = 0,29 (1 – 0,5 × 0,29) = 0,248 – для арматуры класса В500; αm = 0,25 (1 – 0,5 × 0,25) = 0,219 – для арматуры класса А400; h 0 =
Полная высота сечения плиты при диаметре арматуры d = 10 мм и толщине защитного слоя 10 мм h'f = h 0 + a = 53,5 + 15 = 68,5 мм, где a = 10 + 5 = 15 мм. Оставляем принятую ранее толщину плиты h'f = 80мм и расчетную высоту сечения h 0= h'f - a = 80 – 15 = 65 мм. Расчет продольной арматуры в плите. Расчеты по определению необходимого количества рабочей арматуры в многопролетной неразрезной плите монолитного перекрытия сведены в табл. 1 для двух вариантов армирования – непрерывного, сварными рулонными сетками из арматуры класса В500 и раздельного, плоскими сварными сетками из арматуры класса А400 (рис. 4, 5). В курсовом проекте достаточно расчета по одному из вариантов армирования.
При расчете продольной арматуры в плите перекрытия на средних участках между осями 2–6 учтено указание[6] о том, что для плит, окаймленных по всему контуру монолитно связанными с ними балками, в сечениях промежуточных пролетов и у промежуточных опор величины изгибающих моментов, а, следовательно, и необходимое количество рабочей продольной арматуры разрешается уменьшать до 20 %. На участках в средних пролетах и над средними опорами
М ср = – Мс = ± 0,8 × 3,66 = ± 2,93 кНм.
Рис. 5
При выборе сеток в табл. 1 учтено указание п. 1.6 ГОСТ 8478-81 о том, что вследствие ограниченной номенклатуры стандартных сеток, разрешается изготовление нестандартных, при условии, что диаметры всех продольных рабочих стержней будут одинаковыми, не превышающими 5 мм в рулонных сетках (при арматуре класса А400 6 мм), диаметры всех поперечных стержней будут также одинаковыми, не превышающими 8 м как в рулонных, так и в плоских сетках. При армировании разрешается разрезка сеток.
II. ПРОЕКТИРОВАНИЕ СБОРНОГО ЖЕЛЕЗОБЕТОННОГО ПЕРЕКРЫТИЯ
Расчет плиты П-1
Расчет плиты перекрытия в целом заключается в расчете ее полки, поперечного и продольного ребер. Расчет полки плиты. Полка плит марок П представляет собой четыре прямоугольные ячейки в плане (см. рис. 10) со сложным характером опирания сторон. В поперечном направлении полка защемлена в продольных ребрах,а в продольном направлении она работает как неразрезная многопролетная конструкция, опорами которой являются поперечные ребра.
продольных и поперечных ребрах. За расчетные пролеты принимаются: в коротком направлении (пролет в свету) l 1 = b¢f – 2 b 1 = 1285 – 90 × 2 = 1105 мм (рис. 11); в длинном направлении l 2 = l – b 2 = 1385 – 85 = 1300 мм, где b 1 и b 2 – ширина поверху продольного и поперечного ребер соответственно. Соотношение сторон полки плиты Нагрузка на полосу плиты с условной шириной 1,0 м при толщине плиты 50 мм по п. 5.3 [1], кН/м:
Изгибающий пролетный момент в полке плиты на 1 м ширины с целью упрощения расчета вычислим по формуле
М = М 0 = М 1 = М 2 =
допуская соотношение сторон равным 1 (фактически
М =
а от постоянных и длительных М l = 0,8 .14,5 . 1,32/48 = 0,408 кНм = = 408000 Нмм.
Рис. 12
Допускается, что М 1 = М 2 = – M ¢I = – M I = – M II = – M¢ II. М l /М = 408000 / 458000 = 0,89 < 0,9, необходимо учитывать согласно п. 3.3 [3] коэффициент условий работы γ b 1=1. Панель проектируем из бетона класса В20 с характеристиками: Rb = 11,5 МПа; Rbt = 0,90 МПа; Rb ser = 15,0 МПа; Rbt ser = 1,35 МПа; Еb = 27500 МПа с учетом тепловой обработки бетона. В качестве рабочей арматуры используем проволоку класса В500 с расчетным сопротивление Rs = 415 МПа; Еs = 200000 МПа в плите в виде сварных рулонных сеток с продольной и поперечной рабочей арматурой, а в продольных и поперечных ребрах – стержневую арматуру класса А400 в виде плоских сварных каркасов с Rs = 355 МПа. Поперечную арматуру в ребрах панели принимаем класса Уточняем толщину плиты, приняв коэффициент армирования m s = 0,006:
или по табл. прил. 1 настоящего учебного пособия
Учитывая рекомендации п.5.4 и 5.7 [3], принимаем плиту толщиной 50 мм с h 0 = 50 – 15 = 35 мм. Определим площадь сечения арматуры на 1 м ширины плиты при
Принимаем рулонную сетку С-3 марки
Рис. 13
Расчет промежуточного поперечного ребра. Поперечные ребра панели монолитного связаны с продольными ребрами, однако, учитывая возможность поворота их при действии внешней нагрузки, за расчетную схему поперечного ребра в запас прочности принимаем балку со свободным опиранием. Расчетный пролет поперечного ребра исчисляется как расстояние между осями продольных ребер (рис. 14): Согласно рекомендациям [12] принимаем высоту поперечных ребер 200 мм, ширину по низу – 60 мм, по верху – 85 мм. Максимальная нагрузка на среднее поперечное ребро передается с треугольных грузовых площадей Ас = 0,5 l 12 (рис. 14). Треугольную нагрузку допускается заменить на эквивалентную равномерно распределенную по формуле
а временная эквивалентная соответственно
где
Рис. 14
Суммарная равномерно распределенная нагрузка
Расчетные усилия
В том случае, когда пролет
При отношении толщины плиты к высоте ребра
Необходимое количество продольной арматуры класса А400 при
По таблице 3.2 [3] находим α R =0,39. Так как α m = 0,0128 < α R, сжатая арматура по расчету не требуется.
Принимаем в поперечных ребрах плоские сварные каркасы с продольной арматурой из стержней диаметром 8 мм с Аs = 50,3 мм2. Проверим прочность наклонной полосы между наклонными сечениями. При Q = 7,87 . 0,95 = 7,48 кН < При высоте ребра 20 см и продольной арматуре Æ 8мм принимаем поперечные стержни в каркасах из арматуры класса А240 диаметром 6мм с Аs =28 мм2. В соответствии с п.5.21 [3] шаг арматуры должен быть не более Прочность наклонных сечений поперечных ребер по поперечной силе проверим согласно п.3.31 [3]. Поскольку
Мb = 1,5 Rbt bh 02 = 1,5 . 0,81 . 60 . 1752 = 2,48.106 Нмм.
Определим длину проекции невыгоднейшего наклонного сечения:
q 1 = q – 0,5 qv = 13,175 – 0,5 . 11,41 = 7,47 кН/м(н/мм).
Поскольку
следует принимать
с =
Принимаем c 0 = c = 212 мм. Тогда
Qsw =0,75 qsw . c 0 =0,75 . 63,47 . 212 = 10091,7Н; Qb =
Qb + Qsw = 11698 + 10091 = 21789Н = 21,79кН > Q = Q max – q 1. с = = 7,48 – 7,47 . 0,212 = 5,9кН, т. е. прочность наклонных сечений обеспечена. Проверим требование п. 3.35 [3]
т. е. требование выполнено.
Расчет продольного ребра. Высоту продольных ребер ориентировочно определяем из соотношений
Погонная нагрузка на два продольных ребра, кН/м:
Полная нагрузка, Н/м: нормативная qn = 3,970 + 15,540 = 19,510, расчетная q = 4,419 + 18,648 = 23,067, в том числе кратковременно действующая часть нормативной нагрузки
длительно действующая нормативная нагрузка
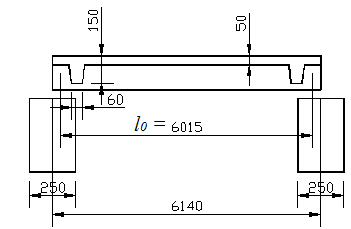
За расчетную схему для продольных ребер принимаем однопролетную балку со свободным опиранием концов на ригели (рис. 15), расчетный пролет определяется как расстояние между серединами площадок опирания ребер панели на ригели (рис. 16).
Рис. 15
Рис. 16
Усилия в двух продольных ребрах: от расчетных нагрузок
от нормативных нагрузок
в том числе, от кратковременной
Qshn = 0,5. 1,943 . 6,02 = 5,85кН;
Длительной
Qln = 58,73 – 5,85 = 52,88кН.
Расчетное сечение двух продольных ребер – тавровое с полкой в сжатой зоне. Ширина полки, вводимая в расчет, в соответствии с п. 3.26 [3] при наличии поперечных ребер
b´f ≤ 1285 мм.
Расчетная высота сечения В соответствии с п. 6.2.10 [2] размеры сечения изгибаемых элементов должны обеспечивать прочность наклонных сечений на действие поперечной силы по наклонной полосе между возможными наклонными трещинами (см. проверку ниже).
Расчет прочности нормальных сечений. Поскольку Мln /Мn= 79,58 / 88,38 = 0,9004 > 0,9, необходимо учитывать согласно п.3.3 [3] коэффициент условий работы γ b 1 = 0,9. Бетон класса В20 с характеристиками:0,9 Rb = 0,9 × 11,5 = = 10,35 МПа; 0,9 Rbt = 0,9 × 0,90 = 0,81 МПа; Rb ser = 15,0 МПа; Rbt ser = = 1,35 МПа; Еb = 27500 МПа с учетом тепловой обработки бетона. Работу бетона в швах замоноличивания в запас прочности условно не учитываем, предполагая, что при неблагоприятных условиях надежная совместная работа бетона замоноличивания с продольными ребрами за счет их сцепления может быть не обеспечена. Тогда расчетная ширина полки
Расчет производим в предположении, что сжатая арматура по расчету не требуется
т. е. нейтральная ось проходит в пределах полки (х < h¢f) и элемент рассчитывается как прямоугольный с шириной b¢f = 1265 мм. Необходимое количество продольной арматуры класса А400 при т. е. сжатая арматура по расчету действительно не требуется
Принимаем стержневую арматуру из стержней 2Æ22А400 с Аs ф = 760 мм2 > 689 мм2. Монтажную арматуру каркасах продольных ребер принимаем класса А240 диаметром 10мм c A ' s = 78,5 . 2=157 мм2 = 0,00016 м2.
Расчет прочности наклонных сечений продольных ребер. При Q min = Q = 69,43 кН > 0,5 Rbtbh 0 = 0,5 × 0,81 × 103 · 0,17 ´ ´ 0,415 = 28,57 кН, поперечная арматура в балке должна ставиться по расчету. Принимаем поперечную арматуру класса A240 с Rsw = 170 МПа (см. табл. 2.6 [3]). В двух плоских каркасах при диаметре стержней продольной арматуры 22 мм поперечные стержни из условия технологии сварки принимаем диаметром 6 мм (dw ≥ 0.25· d, см. п. 9. ГОСТ 14098-91), при Asw = 2 . 28,3 = 57 мм2 (2 Æ 6). Максимально допустимый шаг поперечных стержней у опор в соответствии с п. 5.21 [3] при h 0 = 450–35 мм = 415 мм: s £ 0,5 h 0 = = 0,5 · 415 = 207 мм; s £ 300 мм. Кроме того, в соответствии с п. 3.35 [3]
Принимаем шаг поперечных стержней в каркасах s = 150мм на приопорных участках и 300 мм (0,75 h 0 = 0,75 · 0,415 = 311 мм) на средних. Расчет прочности по полосе между наклонными сечениями. Расчет прочности по наклонной полосе между наклонными сечениями производим из условия 3.43 [2]. Q ≤ 0,3 Rbbh 0, где Q принимается на расстоянии не менее h 0 от опоры; 0,3 Rbbh 0 = 0,3 · 10,35 · 103 · 0,17 · 0,415 = 219,1 кН > > Q = Q – qh 0 = = 69,43 – 23,07 · 0.415 = 59,86 кН, т. е. прочность наклонной полосы на сжатие обеспечена. Расчет прочности на действие поперечной силы по наклонному сечению.
(см. формулу (3.48) [3]). Так как qsw = 64,6 кН/м > 0,25 Rbtb = 0,25 · 0,81 · 1000 · 0,17 = = 34,42 кН/м, Mb = 1,5 Rbtbh 02 = 1,5 · 0,81 · 1000 · 0,17 · 0,4152 = = 35,57 кН·м (см. п. 3.31 и формулу (3.46) [3]). Определяем длину проекции невыгоднейшего наклонного сечения c. При расчете элемента на действие равномерно распределенной нагрузки q значение c принимают равным
Так как
Принимаем длину проекции невыгоднейшего наклонного сечения c = 1,24м. Длину проекции наклонной трещины c 0принимают равным c, но не более 2 h 0 = 0,415 · 2 = 0,83 м (см. п. 3.31 [3]). Принимаем длину проекции наклонной трещины c 0 = c = 0,83м. Тогда
Поперечную силу, воспринимаемую бетоном, определяют по формуле Qb, min = 0,5 Rbtbh 0 (см. п. 3.31 [3]).
Qb, min = 0,5 Rbtbh 0 = 0,5 · 0,81 · 103 · 0,17 · 0,415 = 28,57кН < < = 2,5 · 0,81 · 103 · 0,17 · 0,415 = 142,86 кН.
Принимаем Расчет изгибаемых элементов по наклонному сечению производят из условия
Q =
При Qsw + Qb = 40,21 + 42,86 = 83,07 кН > Q = 53,95 кН, прочность наклонных сечений обеспечена (см. п. 3.31 [3]).
Поскольку продольная растянутая арматура ребер по концам приварена к закладным деталям, проверку наклонных сечений на действие момента не производим.
Расчет ширины раскрытия наклонных трещин. (Расчет выполнен на основе примера приведенного в статье «Расчет трещиностойкости железобетонных конструкций по новым нормативным документам» в журнале «Бетон и железобетон», 2003г). Расчет железобетонных элементов третьей категории трещиностойкости по второй группе предельных состояний производится на действие нормативных нагрузок с коэффициентом надежности по нагрузке γ ƒ =1,0. Расчет производим по формуле
где φ s 1 – коэффициент, учитывающий продолжительность действия нагрузки (при непродолжительном действии равен 1, при продолжительном – 1.4); φ s 2 – коэффициент, учитывающий профиль поперечной арматуры (для гладкой арматуры равен 0,8, для арматуры периодического профиля – 0,5); Напряжения в поперечной арматуре σ sw определяют, принимая, что поперечная сила, воспринимаемая бетоном, отвечает своему минимальному значению Qb. min = 0,5 .Rbt.ser .b. h 0, и, следовательно, поперечная сила, передаваемая на поперечную арматуру, составляет Q – Qb min. При этом поперечную арматуру, воспринимающую эту силу, учитывают на длине проекции наклонного сечения с = h 0, т. е. равный ее минимальному значению. Тогда, Выполнив вычисления, получим:
Qb .min = 0,5 .1,35 .170. 415 = 47621 Н;
| |||||||||||||||||||
|
| Поделиться: |


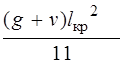 =
=  = 4,8 кНм;
= 4,8 кНм; = ±
= ± 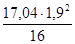 = ± 3,85 кНм;
= ± 3,85 кНм; = -
= - 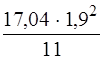 = - 5,6 кНм;
= - 5,6 кНм;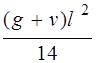 = -
= - 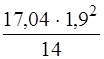 = - 4,394 кНм,
= - 4,394 кНм, = m
= m 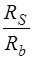 = 0,006
= 0,006  = 0,29< x R = 0,502 – для арматуры класса В500; x = 0,006
= 0,29< x R = 0,502 – для арматуры класса В500; x = 0,006  = 0,25 < x R = 0,531 – для арматуры класса А400, где x R определяется по табл. 3.2 [3].
= 0,25 < x R = 0,531 – для арматуры класса А400, где x R определяется по табл. 3.2 [3].


 =
= 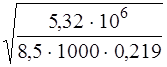 = 53,5 мм.
= 53,5 мм.

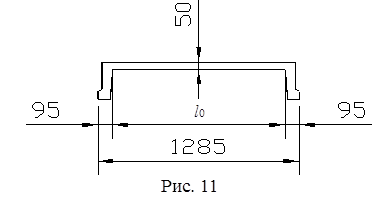 С целью упрощения расчета каждую из ячеек полки в статическом отношении условно рассматриваем как плиту, опертую по контуру, с частичным защемлением в
С целью упрощения расчета каждую из ячеек полки в статическом отношении условно рассматриваем как плиту, опертую по контуру, с частичным защемлением в , l 1 = l 0 (см. рис. 11).
, l 1 = l 0 (см. рис. 11).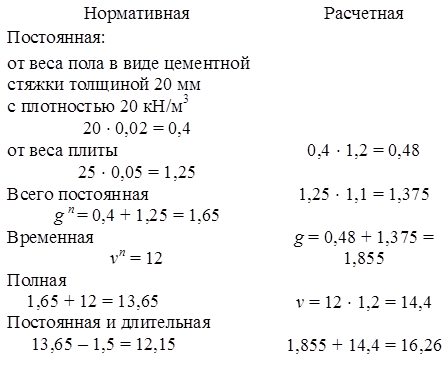
 ,
,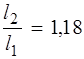 ) и, следовательно, опорные моменты равными пролетным (рис. 12). Коэффициент h = 0,8 учитывает благоприятное влияние распора в жестком контуре. Тогда момент от полной нагрузки составит:
) и, следовательно, опорные моменты равными пролетным (рис. 12). Коэффициент h = 0,8 учитывает благоприятное влияние распора в жестком контуре. Тогда момент от полной нагрузки составит: кНм = 458000 Нмм,
кНм = 458000 Нмм,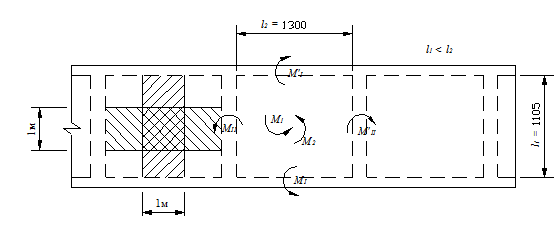
 ;
;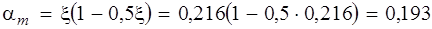
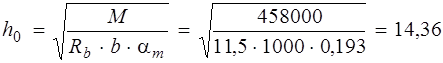 мм;
мм;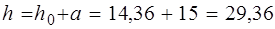 мм.
мм.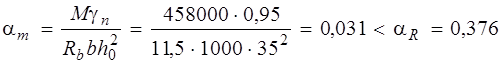 (п. 3.2 [2]), т. е. сжатая арматура по расчету не требуется
(п. 3.2 [2]), т. е. сжатая арматура по расчету не требуется
 с продольной и поперечной рабочей арматурой площадью Аs ф = 47,0 мм2; сетка С – 3 раскатывается вдоль продольных ребер на всю ширину полки. Дополнительная сетка С – 4 заводится в продольные ребра на длину, равную
с продольной и поперечной рабочей арматурой площадью Аs ф = 47,0 мм2; сетка С – 3 раскатывается вдоль продольных ребер на всю ширину полки. Дополнительная сетка С – 4 заводится в продольные ребра на длину, равную  (рис. 13).
(рис. 13).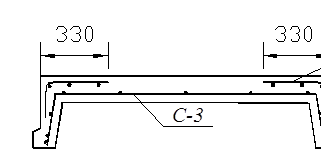
 мм.
мм.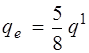 , тогда полная эквивалентная нагрузка составит
, тогда полная эквивалентная нагрузка составит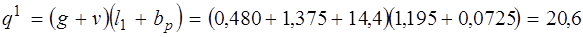 кН/м,
кН/м, кН/м,
кН/м,
 мм – средняя толщина поперечного ребра; g и v – выбираются из таблицы сбора нагрузок. Собственный вес поперечного ребра
мм – средняя толщина поперечного ребра; g и v – выбираются из таблицы сбора нагрузок. Собственный вес поперечного ребра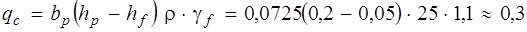 кН/м.
кН/м.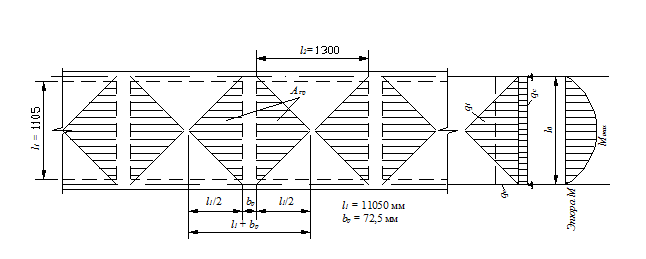
 кН/м.
кН/м.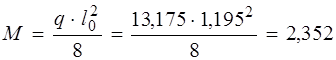 кНм = 2,352 × 106 Н×мм;
кНм = 2,352 × 106 Н×мм; кН.
кН. , грузовая площадь имеет вид трапеции. Расчетные формулы преобразуется так:
, грузовая площадь имеет вид трапеции. Расчетные формулы преобразуется так: ;
;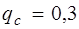 кН/м;
кН/м;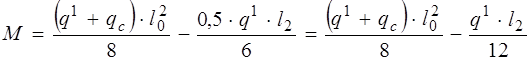 ;
; .
.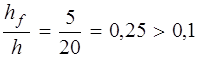 согласно п. 3.26 [3] за расчетное сечение поперечного ребра принимаем тавровое с шириной полки в сжатой зоне
согласно п. 3.26 [3] за расчетное сечение поперечного ребра принимаем тавровое с шириной полки в сжатой зоне мм <
мм < мм.
мм.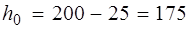 мм
мм .
. мм2.
мм2.
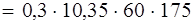 Н
Н  = 32,6 кН прочность полосы обеспечена.
= 32,6 кН прочность полосы обеспечена. 87,5 мм и не более 300 мм. Принимаем sw =75мм.
87,5 мм и не более 300 мм. Принимаем sw =75мм.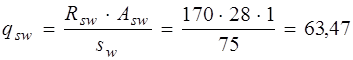 Н/мм > >
Н/мм > >  Н/мм, хомуты необходимо учитывать в расчете полностью и значение Мb определяется по формуле
Н/мм, хомуты необходимо учитывать в расчете полностью и значение Мb определяется по формуле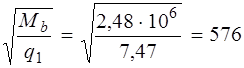 мм < <
мм < < 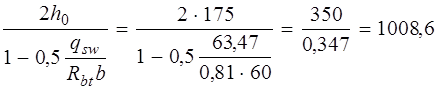 мм,
мм,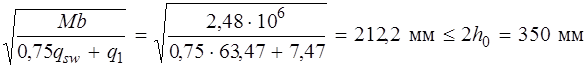 .
.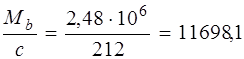 Н;
Н; мм > Sw =75 мм,
мм > Sw =75 мм,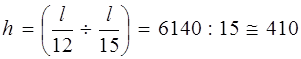 мм. Полученное значение высоты округляем в большую сторону с кратностью 50 мм, но ограничиваем h £ 450 мм. Окончательно принимаем h = 450 мм. В качестве опорных конструкций для панелей принимаем ригели прямоугольного сечения с шириной ребра 25 см.
мм. Полученное значение высоты округляем в большую сторону с кратностью 50 мм, но ограничиваем h £ 450 мм. Окончательно принимаем h = 450 мм. В качестве опорных конструкций для панелей принимаем ригели прямоугольного сечения с шириной ребра 25 см.
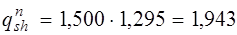 ;
;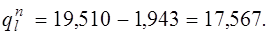
 мм = 6,02 м.
мм = 6,02 м.
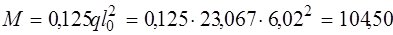 кНм=104,50 × 106 Н×мм;
кНм=104,50 × 106 Н×мм;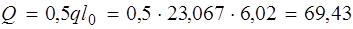 кН;
кН; кНм;
кНм; кН;
кН;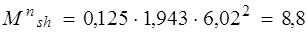 кНм;
кНм;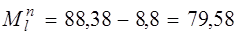 кНм;
кНм; см. При ширине продольных ребер по верху 95 мм и по низу 75 мм суммарная толщина двух ребер в уровне центра тяжести арматуры без учета швов замоноличивания будет равна 170 мм.
см. При ширине продольных ребер по верху 95 мм и по низу 75 мм суммарная толщина двух ребер в уровне центра тяжести арматуры без учета швов замоноличивания будет равна 170 мм. мм.
мм. = 0:
= 0: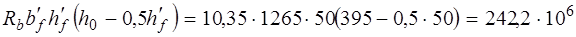 Н×мм = = 242,2 кНм > М = 104,50 кНм
Н×мм = = 242,2 кНм > М = 104,50 кНм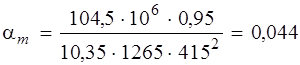 < α R = 0,39,
< α R = 0,39, мм2.
мм2.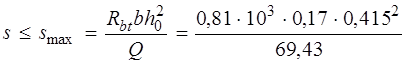 = 0,342 м.
= 0,342 м. кН/м
кН/м , а если при этом
, а если при этом 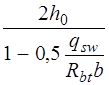 или
или 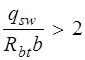 , следует принимать
, следует принимать (см. п. 3.32 [3]).
(см. п. 3.32 [3]).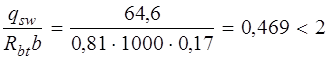 .
.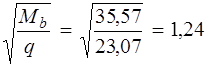 м > >
м > > 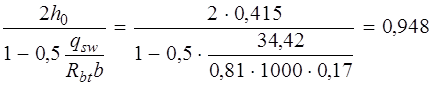 м,
м, м, но не более 3 h 0 = 3 · 0,415 = 1,245 м (см. п. 3.32 [3]).
м, но не более 3 h 0 = 3 · 0,415 = 1,245 м (см. п. 3.32 [3]).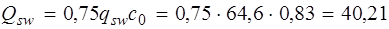 кН.
кН. , но не более Qb ,max = 2,5 Rbtbh 0 и не менее
, но не более Qb ,max = 2,5 Rbtbh 0 и не менее кН < Qb ,max = 2,5 Rbtbh 0 =
кН < Qb ,max = 2,5 Rbtbh 0 =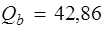 кН.
кН.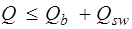 , где Q – поперечная сила в наклонном сечении с длиной проекции c; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем на расстоянии c от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длиной c.
, где Q – поперечная сила в наклонном сечении с длиной проекции c; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем на расстоянии c от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длиной c.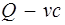 = 69,43 – 18,65 · 0,83 = 53,95 кН.
= 69,43 – 18,65 · 0,83 = 53,95 кН.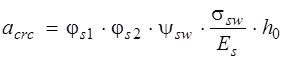 ,
,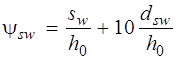 , где
, где  – относительное расстояние между поперечными стержнями;
– относительное расстояние между поперечными стержнями;  – относительное значение диаметра поперечной арматуры.
– относительное значение диаметра поперечной арматуры. где, Asw – площадь сечения поперечной арматуры, расположенной в одной нормальной к продольной оси элемента плоскости, пересекающей наклонное сечение.
где, Asw – площадь сечения поперечной арматуры, расположенной в одной нормальной к продольной оси элемента плоскости, пересекающей наклонное сечение.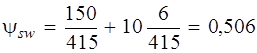 ;
; МПа;
МПа;


