Условия равновесия и устойчивости термодинамических систем: равновесие трехфазной системы. Правило фаз Гиббса. Фазовые переходы 1-го рода. Уравнение Клапейрона-Клаузиуса. Фазовая диаграмма состояния.

Равновесие трехфазной системы.

1) Каждая из фаз должна находиться в состоянии равновесия.

2) Для каждой пары фаз должно соблюдаться условие равновесия:

Очевидно, что для трехфазной системы равновесие может быть в одной точке. Подобные точки называются тройными точками. Однокомпонентные системы не могут существовать в более чем трех фазах. Точка, где существуют твердая, жидкая и парообразная фаза называется основной тройной точкой. Она также является важной характеристикой.

Правило фаз Гиббса.

Гиббс вывод частной распространил на системы многофазную многокомпонентную.

Пусть мы имеем систему, состоящую из Ф фаз и К компонентов.

Аргументов .

Уравнений .

.

Число степеней свободы:

.

- Правило фаз Гиббса.

Фазовые переходы 1-ого рода.

Фаза – гомогенная область в гетерогенной системе ограниченная поверхностью раздела. Фазовый переход первого рода: переход вещества из одной фазы в другую.

Фазовый переход 1-ого рода – такой переход, когда первые производные от энергии Гиббса имеют скачок.

Фазовый переход – это мирное существование двух фаз.

T,P=const.

То есть фазовый переход всегда характеризуется теплотой фазового перехода.

Тогда продифференцируем и получаем:

p_s и T_s – температура и давление насыщения.

- уравнение Клайперона-Клаузиуса.

Фазовая диаграмма состояния.

В области фазовой диаграммы проводятся кривые фазового равновесия. Кривая фазового равновесия называется кривая соответствующая равновесию двух фаз.

16. Фазовая диаграмма состояния рТ. Фазовые диаграммы состояния: рv-, Ts-, hs-

Фазовая диаграмма — термодинамическая диаграмма, в которой по осям координат откладываются физические параметры (давление и температура, давление и удельнй объём и т.д.) и наносятся кривые фазового равновесия.

Диаграмма состояния (фазовая диаграмма) - диаграмма, изображающая зависимость устойчивого фазового состояния одно- или многокомпонентного вещества от термодинамич. параметров, определяющих это состояние (температуры T, давления P). Каждая точка фазовой диаграммы указывает на фазовый состав вещества при заданных значениях термодинамич. параметров. В зависимости от числа внеш. параметров фазовая диаграмма может быть двумерной, трёхмерной и многомерной.

Фазовые диаграммы однокомпонентных систем изображаются на плоскости в координатах p–T. На них присутствуют поля, отвечающие существованию той или иной фазы вещества (газообразной, жидкой, различных твердых модификаций), разделенные линиями фазового равновесия, вдоль которых возможно сосуществование граничащих фаз. Места, где сходятся три различные линии фазовых равновесий, образуют так называемые тройные точки, в которых могут сосуществовать три фазы. Это максимальное число фаз, способных равновесно сосуществовать в однокомпонентных системах.

Кривая фазового равновесия — кривая, соответствующая равновесному состоянию фаз. рϑ-диаграмма реальной ТС Её особенностью является (как и 2 следующих диаграмм) изображение области 2-фазного равновесного состояния в виде площадей, ограниченных пограничными кривыми

На pv - диаграмме представлены (рис. 2.3, а):

- р, v - давление Па, удельный объем м3/кг;

- vo - удельный объем воды при t = 0 oC;

- - удельный объем воды при ts и pi = const;

- - удельный объем сухого насыщенного пара при ts и pi = const;

- - удельный объем влажного пара, соответствующего состоянию в точке Аi,

- хАi - степень сухости пара, соответствующая состоянию пара в точке Аi;

Тs-диагр амма реальной ТС

 

 

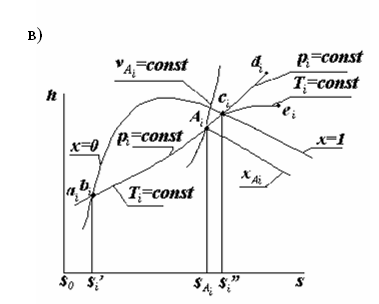
hs-диаграмма реальной ТС

 

На Ts- и hs - диаграммах представлены (Рис. 2.3, б и 2.3, в):

- T – температура К; h – удельная энтальпия, Дж/кг; s - удельная энтропия Дж/(кгּК);

- h’i – удельная энтальпия воды при ts и при давлении pi;

- h’’i – удельная энтальпия сухого насыщенного пара при ts и при давлении pi;

- so - удельная энтропия воды при температуре 0оС и при давлении pi t;

- - удельная энтропия воды при ts и при давлении pit;

- - удельная энтропия сухого насыщенного пара при ts и при давлении p;

- sA=- удельная энтальпия влажного пара, соответствующая состоянию в точке Ai,

- - удельная энтропия влажного пара, соответствующего состоянию в точке Аi.

 

Диаграммы состояния используют в материаловедении, металлургии, нефтепереработке, химической технологии (в частности, при разработке методов разделения веществ), производствах электронной техники и микроэлектроники и др. С их помощью подбирают условия промышленного синтеза веществ, определяют направленность процессов, связанных с фазовыми переходами, осуществляют выбор режимов термообработки, отыскивают оптимальные составы фаз и т. п.