
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Временная и фазовая диаграммыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для пользователя основным является визуальное представление модели, в котором элементы описания (уравнения, карты поведений, структурные схемы) представляются в естественной графической форме. В MVS предусмотрена визуализация результатов моделирования при помощи временной (рис. 4) и фазовых диаграмм (рис. 5).
Рис. 4. Временная диаграмма, иллюстрирующая колебания математического маятника
Рис. 5Фазовая диаграмма, иллюстрирующая колебания математического маятника D-анимация Для многих моделей (особенно моделей механических систем) пользователь может получить больше всего информации из непосредственного наблюдения трехмерного динамического изображения моделируемой системы. В визуальной модели для этого предназначено окно 3D-анимации. Окно 3D-анимации позволяет строить динамические трехмерные изображения, в виде совокупности трехмерных примитивов (линия, шар, цилиндр, конус и т.д.), некоторые параметры которых (координата, радиус, цвет и т.п.) однозначно связаны со значением соответствующих переменных модели (рис. 6).
Рис. 6. 3D-анимация, иллюстрирующая колебания математического маятника D-анимация Несмотря на все богатство возможностей 3D-анимации, двумерная анимация не теряет своего значения для пакетов визуального моделирования. Это прежде всего касается разного рода динамических блок-схем и панелей управления, которые по своей природе являются двумерными. Имеется набор стандартных 2D-компонентов: линейные индикаторы, стрелочный индикатор, линейный движок, поворотный регулятор, цветовой индикатор, кнопки. Можно перемещать 2D-компоненту в пределах окна анимации, а также изменять размер компоненты (рис. 7).
Рис. 7. 2D-анимация Интерактивными 2D-компонентами являются Ползунок, «Круговой регулятор» и «Кнопка». Остальные компоненты позволяют только отображать текущее значение переменной. Например, используя две компоненты «Линейный индикатор сплошной» для индикации значений переменных Alpha и Omega можно получить следующую картинку (рис. 8).
Рис. 8. Линейный индикатор сплошной
В заключение хотелось бы отметить, что такие достоинства среды MVS, как простота создания моделей для любого уровня пользователей; повторное использование уже созданных и подтвердивших свою работоспособность моделей на основе использования технологии объектно-ориентированного моделирования.
2.3. Общая схема моделирования в среде MVS на примере модели «Хищник-жертва» предметной области «Биология» В качестве примера, иллюстрирующего возможности исследования математических моделей средствами MVS, рассмотрим моделирование динамики популяций «хищник-жертва», учитывая основные этапы моделирования. Первый этап. ПОСТАНОВКА ЗАДАЧИ Описание задачи Пусть в некотором замкнутом районе живут хищники и жертвы, например, зайцы и волки. Зайцы питаются растительной пищей, имеющейся всегда в достаточном количестве. Волки могут питаться лишь зайцами. Требуется определить продолжительность жизнедеятельности популяции в зависимости от исходных параметров, установить характер процесса изменения численности жертв и хищников во времени. Цели моделирования:
Второй этап. РАЗРАБОТКА МОДЕЛИ Математическая модель Следует отметить, что поведение организмов в живой природе гораздо труднее описать средствами математики, чем самые сложные физические процессы, то есть представить модель в виде уравнения, системы уравнений, системы неравенств, дифференциального уравнения или системы дифференциальных уравнений. В то же время созданные модели помогают установить некоторые закономерности и общие тенденции развития экологических систем. Одним из самых известных примеров описания динамики взаимодействующих популяций являются уравнения Волтерра – Лотка [24]. Рассмотрим модель взаимодействия хищников и их добычи, когда между особями одного вида нет соперничества. Пусть Таким образом, система Волтерра – Лотка имеет вид:
где Непрерывное поведение в общем случае задается совокупностью обыкновенных дифференциальных уравнений. Компьютерная модель При построении компьютерной модели одним из главных моментов является выбор программной среды. В качестве программной среды нами выбрана интегрированная оболочка MVS. Построение компьютерной модели можно представить в виде нескольких последовательных шагов, связанных с переводом описания модели на язык Model Vision Language (MVL), используемого в MVS. Шаг 1. Создание нового проекта. Запустите среду MVS и создайте новый проект с помощью команд основного меню «Проект/Новый…». В появившемся диалоговом окне выберите путь к папке проекта (например, «D:\Мои_модели\»), введите имя проекта Хищник_жертва и нажмите кнопку «Создать». После этого появится папка «D:\Мои_модели\Хищник_жертва» и в ней файл базы данных проекта «Хищник_жертва.mvb» (рис. 9).
Рис. 9. Сохранение проекта Замечание. Предполагается, что для нового проекта открывается новая папка (если используется существующая, то все данные в ней уничтожаются). В то же время с помощью команды «Проект/Сохранить как» вы можете сохранять в той же папке различные модификации данного проекта. В дальнейшем в этой папке появятся еще два файла – «Хищник_жертва.ini» и «Хищник_жертва _em.ini» - в которых сохраняются соответственно установки проекта и выполняемой модели. В имени файла не допустимы знаки: пробел, дефис, тире, плюс, а также другие недопустимые символы. В составном имени файла целесообразно использовать знак подчеркивания. Итак, после создания проекта у вас должно быть в наличии 3 файла, хранящихся в папке проекта: 1. *.mvb 2. *.ini 3. *_em.ini Перед вами откроется основное окно проекта с четырьмя дочерними окнами (рис. 10): 1) Окно управления проектом (слева вверху), содержащее дерево основных составляющих проекта. В новом проекте по умолчанию добавлен класс непрерывного блока, например, «Хищник_жертва» (имя класса совпадает с именем проекта). 2) Окно виртуального стенда (в центре вверху. По умолчанию в виртуальный стенд помещен экземпляр класса «Хищник_жертва» с именем «Хищник_жертва_1». Рассматриваемая биологическая модель является изолированной системой, и нет особой необходимости в структурной схеме и блоках. Однако данная версия пакета ориентирована на блочное моделирование и потому изолированная система представляется как блок без входов и выходов, а ее модель в виде виртуального стенда с экземпляром такого блока. 3) Окно редактирования добавленного по умолчанию класса (в данном случае класса «Хищник_жертва») содержит дерево составляющих описания класса. Поскольку данный блок предполагается непрерывным, то по умолчанию в него добавлена пустая система уравнений с именем «Система_уравнений_1». 4) Окно редактирования системы уравнений, открытое на пустой «Система_уравнений_1».
Рис. 10. Многооконный интерфейс MVS. Шаг 2. Ввод и описание всех необходимых параметров. Описывая моделируемую систему необходимо выделять не просто всю совокупность параметров, характеризующую состояние объекта в некоторый момент, а разбивать их на следующие группы: параметры (параметры, не меняющиеся для данного экземпляра класса); внутренние переменные (параметры, меняющиеся для данного экземпляра класса и характеризующие поведение объекта; константы (параметры, не меняющиеся для данного класса). Перед тем как вводить переменные и константы необходимо проанализировать систему дифференциальных уравнений, описывающих модель, выделить те переменные, которые присутствуют в системе, а также начальные значения для тех переменных, по которым осуществляется дифференцирование. Характеризуя объект и его свойства, мы используем переменные, которые могут принимать значения различного типа. В данной задаче использованы только вещественные переменные. Для данной модели – это переменные a, b, c, d, x1, x2. Для того чтобы ввести первоначальные значения переменных перейдите в окно редактирования класса «Хищник_жертва», выделите в дереве объектов узел «Внутренние переменные», нажмите правую клавишу мыши вызовите всплывающее меню и выполните команду «Добавить». То же самое можно сделать с помощью команды «Редактировать/Добавить» главного меню или кнопки
Рис. 11. Введние переменных. В появившемся диалоговом окне введите идентификатор переменной a, оставьте заданный по умолчанию тип double и задайте начальное значение, равное 4 и комментарий (рис. 12).
Рис. 12. Окно ввода переменных. Аналогичным образом добавьте переменные b, c, d, x1, x2 (рис. 13).
Рис. 13. Описание класса. Замечание. Вы можете изменить введенные определения дважды кликнув на них мышью, а также с помощью команды «Изменить» всплывающего меню, команды «Редактировать/Изменить» главного меню или кнопки Завершение редактирования происходит по клавише «Enter» или щелчка мыши за пределами редактируемой строки. Отмена редактирования происходит по нажатию клавиши «Esc». Вы можете удалить введенные определения с помощью команды «Удалить» всплывающего меню, команды «Редактировать/Удалить» главного меню или кнопки Шаг 3. Ввод уравнений. Для задания формул и уравнений в пакете предусмотрен специальный редактор, который позволяет вводить математические выражения в близком к естественному виде. В окне редактирования уравнений вызовите специальный редактор формул при помощи двойного щелчка мыши на узле «Уравнения» или команды «Изменить» всплывающего меню. Введите необходимые уравнения (рис. 14)
Рис. 14. Редактор формул.
Система уравнений может включать в себя обыкновенные дифференциальные уравнения первого порядка и алгебраические уравнения. Аналитически разрешенные уравнения (формулы) при отсутствии в них циклов сводятся просто к последовательности операторов присваивания. Вы можете также непосредственно использовать в уравнениях первую и вторую производные, не вводя дополнительных переменных. Если вы не указали, какие переменные являются искомыми (оператор find), то транслятор попытается определить их сам, исходя из контекста задачи: искомыми не могут быть параметры, константы и входы. Транслятор также стремится сделать искомыми (если это возможно) интегрируемые переменные и переменные, стоящие в левых частях формул. Если же транслятору не удается выбрать искомые переменные, то он вызывает специальный диалог и предлагает сделать это вручную. Помимо собственно уравнений и формул в систему уравнений могут быть также включены необходимые комментарии. Комментарий начинается символом «--» (двойной минус) и продолжается до конца строки. Уравнение может быть записано различными способами. Транслятор сам преобразует это уравнение к «канонической» форме, необходимой для численного решения. Шаг 4. Сохранение модели. Шаг 5. Компилирование модели. Перед проведением компьютерного эксперимента необходимо откомпилировать модель с помощью команды основного меню «Модель/Пуск» или кнопки Пакет MVS относится к категории компилирующих: для элементов описания моделируемой системы генерируется “код” на промежуточном языке программирования, который затем компилируется в машинный код и связывается с Run Time Library (RTL) MVS с помощью штатного компилятора командной строки этого языка. В данной версии пакета в качестве промежуточного языка используется Borland Object Pascal (Delphi). Третий этап. КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ Шаг 1. Составление плана эксперимента. Рекомендуется наметить следующие эксперименты с моделью: · тестирование – проверка правильности работы модели; · эксперимент 1 – исследование поведения модели при исходных данных, то есть когда количество жертв больше числа хищников; · эксперимент 2 – исследование поведения модели, в том случае, когда количество жертв меньше числа хищников; · эксперимент 3 – исследование поведения модели, в том случае, когда количество жертв равно числу хищников. Шаг 2. Проведение эксперимента. Эксперимент 1. Рассмотрим технологию проведения эксперимента на примере исследования поведения модели при исходных данных, то есть когда количество жертв больше числа хищников. После компиляции модели, то есть после первого запуска модели открывается окно «Визуальная модель MVS» (рис. 15).
Рис. 15. Окно «Визуальная модель MVS» Визуальная модель также как и интегрированная оболочка является многооконным приложением. В заголовке главного окна указывается имя выполняемой модели, которое вы можете изменить в окне виртуального стенда интегрированной оболочки (по умолчанию это имя проекта). В левой части инструментальной панели отображается текущее значение модельного времени. В нижней части главного окна выводится информация о текущем типе совокупной системы уравнений и общем числе уравнений (в случае системы с переключениями они могут изменяться в ходе прогона модели). В MVS предусмотрена стандартная «математическая графика», а именно окно «Временная диаграмма», которое по необходимости можно перенастроить в окно «Фазовая диаграмма», двумерная и трехмерная графика. С помощью команды «Окна/Новая диаграмма» или кнопки Перенесите методом «Drag and drop» в окно диаграммы из окна переменных те переменные, по которым производится дифференцирование, запустите модель при помощи кнопки
Рис. 16. Временная диаграмма Для того чтобы получить фазовую диаграмму создайте новую диаграмму, перетащим в нее те же самые переменные, а затем правой клавишей мыши откройте на ней всплывающее меню и выполните команду «Настройка». В появившемся диалоге настроек укажите с помощью двойного щелчка мышью в поле
Рис. 17. Создание фазовой диаграммы Запустите модель при помощи кнопки Закончите данный прогон с помощью кнопки Переместите окна временной и фазовой диаграмм рядом друг с другом. Запустите модель и получите следующий график (рис. 18).
Рис. 18. Временная и фазовая диаграммы эксперимента 1. Эксперименты 2 и 3 Для проведения остальных экспериментов целесообразно воспользоваться возможностями 2D-анимации, представленными в MVS набором следующих компонентов: линейные индикаторы, стрелочный индикатор, линейный движок, поворотный регулятор, цветовой индикатор, кнопки. Интерактивными 2D-компонентами являются ползунок, поворотный регулятор и кнопка. При помощи ползунка можно интерактивно менять число хищников и жертв в популяции, а цветовой индикатор показывает изменение численности популяции в тот или иной промежуток времени (рис. 19). С помощью команды «Окна/Новая 2D-анимация» создайте анимационное окно. Откройте с помощью кнопки
Рис. 19. Стандартные 2D-компоненты. Выберите на этой панели компоненту «Ползунок» и методом «Drag and drop» перетащите ее в левую часть окна анимации. Щелкните на появившемся изображении ползунка правой клавишей мыши и с помощью команд всплывающего меню установите вертикальное расположение ползунка, режим показа числового значения и интервал значений 0.. 6. С помощью мыши можно перемещать 2D-компоненту в пределах окна анимации, а также изменять размер компоненты. Щелкните правой клавишей мыши сверху от компоненты и, выполнив команду «Добавить надпись» всплывающего меню, создайте пояснительную надпись для ползунка. Надпись также можно перемещать с помощью мыши, не отпуская левую клавишу. Теперь необходимо связать ползунок с переменной модели. Делается это методом «Drag and drop». Переместите переменную x1 из окна переменных и бросьте ее на изображении ползунка. Теперь ползунок будет отображать текущее значение переменной x1, а при перемещении ползунка с помощью мыши присваивать соответствующее значение этой переменной. Аналогичным образом создайте ползунок для переменной x2. Остальные компоненты позволяют только отображать текущее значение переменной. Используйте две компоненты «Линейный индикатор сплошной» для индикации значений переменных x1 и x2 (рис. 20).
Результаты экспериментов 2 и 3 представлены на рисунках 21 и 22.
Рис. 22. Результаты эксперимента 3.
Четвертый этап. АНАЛИЗ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ После проведения каждого эксперимента необходимо проанализировать получившиеся результаты. В итоге целесообразно проследить влияние изменяемых параметров на поведение модели в целом. Анализ результатов эксперимента 1 (рис. 18): Видно, что процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов 3:1 обе популяции сначала растут. Когда число хищников достигает величины Аналогичным образом производится анализ результатов экспериментов 2 и 3, исходя из временной и фазовых диаграмм (рис. 21 и 22). В данном параграфе мы продемонстрировали все этапы создания и исследования математической модели экологической системы «хищник-жертва» с помощью интегрированной оболочки MVS. 2.4. Задания на моделирование процессов из различных предметных областей в среде MVS.
Задание. 1) Выберите определенную предметную область и модель, относящуюся к этой области. 2) Опишите имеющуюся задачу, опираясь на образец, рассмотренный в предыдущем параграфе. 3) Сформулируйте цели моделирования, реализация которых позволит провести количественный и качественный анализ влияния параметров, входящих в модель на ее поведение. 4) Изучите представленную математическую модель, и на её основе постройте компьютерную модель в среде MVS: 1. создайте проект; 2. введите и опишите все необходимые параметры, переменные, константы, функции или др. объекты; 3. введите уравнение или систему дифференциальных уравнений; 4. сохраните и прокомпилируйте модель; 5. постройте временную диаграмму; 6. постройте фазовую диаграмму, если это целесообразно; 5) Составьте план возможных экспериментов. 6) Проведите эксперименты, воспользовавшись возможностями 2D-анимации (ползунок, линейный индикатор сплошной и др.). 7) Создайте 3D-анимацию, если изучаемая система подразумевает построение наглядного трехмерного изображения, опираясь на «Руководство пользователя». 8) Создайте план прогона для данной компьютерной модели, опираясь на «Руководство пользователя», который будет отражать все проведенные эксперименты на временной или фазовой диаграммах. 9) Изучите особенности работы модели в течение модельного времени и работы согласно плану. 10) Создайте карту поведения, опираясь на «Руководство пользователя». 11) Проанализируйте полученные результаты.
Предметная область «Физика» Модель «Движение пули» [16] Математическая модель. Пуля, двигаясь со скоростью
Знак минус взят в связи с тем, что сила сопротивления стены направлена в сторону, противоположную направлению скорости. Модель «Радиоактивный распад» [25] Математическая модель. Радиоактивным распадом называются самопроизвольные превращения ядер атомов некоторых элементов в ядра других элементов, сопровождающимися альфа-, бета- и гамма-излучением. Радиоактивный распад носит статистический характер: ядра атомов распадаются не одновременно все сразу, а в течение всего времени существования данного изотопа. При этом установлено, что количество атомов распадающихся в единицу времени, составляет определенную, постоянную для каждого изотопа часть его нераспавшихся атомов. Эта часть называется постоянной распада и обозначается буквой Таким образом, число атомов
Знак минус показывает, что число Модель «Охлаждение тела» [15, 16] Математическая модель. Природа переноса тепла от чая к окружающему пространству сложна и в общем включает в себя механизмы конвекции, излучения, испарения и теплопроводности. В том случае, когда разность температур между объектом и окружающей средой не очень велика, скорость изменения температуры объекта можно считать пропорциональной этой разности температур. Это утверждение более строго можно сформулировать на языке дифференциального уравнения:
где Модель «Поглощение света при прохождении через воду» [16] Математическая модель. Поглощение светового потока тонким слоем воды пропорционально толщине слоя и потоку, падающему на его поверхность. Обозначим через
где Модель «Ионизация газа» [16] Математическая модель. Под действием постоянного излучения в газовой среде происходит процесс ионизации, при котором за одну секунду образуется
Модель «Траектория всплытия подводной лодки» [32] Математическая модель.
Координата
Модель «Свободное падение тела с учетом сопротивления среды» [24] Математическая модель. Скорость падения тела обозначим Сила тяжести тела равна Таким образом, математическая модель движения тел с учетом сопротивления среды следующая:
Изучите модель, учитывая, что падающие тело – это деревянный шар, а среда - воздух. Замечание:
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 940; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.017 с.) |






 и
и  – число жертв и хищников соответственно. Предположим, что относительный прирост жертв равен
– число жертв и хищников соответственно. Предположим, что относительный прирост жертв равен  ,
,  , где
, где  – скорость размножения жертв в отсутствие хищников,
– скорость размножения жертв в отсутствие хищников,  – потери от хищников. Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи
– потери от хищников. Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи  относительная скорость изменения популяции хищников равна
относительная скорость изменения популяции хищников равна  ,
,  , наличие пищи компенсирует убывание, и при
, наличие пищи компенсирует убывание, и при  имеем
имеем  ,
,  .
.
 .
.

 на панели кнопок (рис. 11).
на панели кнопок (рис. 11).


 на панели кнопок. Кроме того, вы можете редактировать выделенное определение как текст с помощью команды «Редактировать/Редактировать как текст (F2)» главного меню или однократного щелчка мыши.
на панели кнопок. Кроме того, вы можете редактировать выделенное определение как текст с помощью команды «Редактировать/Редактировать как текст (F2)» главного меню или однократного щелчка мыши. на панели кнопок.
на панели кнопок.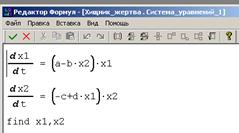
 на панели кнопок.
на панели кнопок.
 можно создать окно диаграммы (по умолчанию это будет временная диаграмма, то есть по оси абсцисс будут откладываться значения модельного времени).
можно создать окно диаграммы (по умолчанию это будет временная диаграмма, то есть по оси абсцисс будут откладываться значения модельного времени).
 , что по оси абсцисс откладываются значения переменной
, что по оси абсцисс откладываются значения переменной  (рис. 17).
(рис. 17).
 или команды «Моделирование/Стоп»
или команды «Моделирование/Стоп» или команды «Моделирование/Рестарт». В результате этих действий данный экземпляр испытуемой системы будет уничтожен и создан новый, снова с начальными значениями переменных. Модельное время снова будет равно 0.
или команды «Моделирование/Рестарт». В результате этих действий данный экземпляр испытуемой системы будет уничтожен и создан новый, снова с начальными значениями переменных. Модельное время снова будет равно 0.
 или команды «Сервис/Стандартные 2D-компоненты» панель 2D-компонент (рис. 19).
или команды «Сервис/Стандартные 2D-компоненты» панель 2D-компонент (рис. 19).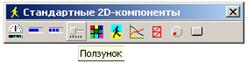


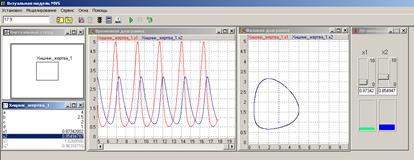 Рис. 21. Результаты эксперимента 2.
Рис. 21. Результаты эксперимента 2. , популяция жертв не успевает восстанавливаться и число жертв начинает убывать. Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников, и, когда число жертв достигает величины
, популяция жертв не успевает восстанавливаться и число жертв начинает убывать. Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников, и, когда число жертв достигает величины  , число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор, пока число хищников не достигнет величины
, число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор, пока число хищников не достигнет величины  . С этого момента начинает расти популяция жертв; через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и процесс повторяется снова и снова. Периодичность процесса явственно видна на фазовой плоскости: фазовая кривая
. С этого момента начинает расти популяция жертв; через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и процесс повторяется снова и снова. Периодичность процесса явственно видна на фазовой плоскости: фазовая кривая  является замкнутой линией. На языке дифференциальных уравнений это означает, что система имеет стационарное состояние, которое достигается в точке
является замкнутой линией. На языке дифференциальных уравнений это означает, что система имеет стационарное состояние, которое достигается в точке  ,
, 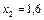 . Если в начальный момент система находилась в стационарной точке, то решения
. Если в начальный момент система находилась в стационарной точке, то решения  не будут изменяться во времени, останутся постоянными. Всякое же другое начальное состояние приводит к периодическому колебанию решений. Неэллиптичность формы траектории, охватывающей центр, отражает негармонический характер колебаний.
не будут изменяться во времени, останутся постоянными. Всякое же другое начальное состояние приводит к периодическому колебанию решений. Неэллиптичность формы траектории, охватывающей центр, отражает негармонический характер колебаний.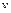 , пробивает стену толщиной
, пробивает стену толщиной  и вылетает из нее. Полагая силу сопротивления стены пропорциональной квадрату скорости движения пули, дифференциальное уравнение имеет вид
и вылетает из нее. Полагая силу сопротивления стены пропорциональной квадрату скорости движения пули, дифференциальное уравнение имеет вид .
.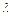 .
. , распавшихся за время
, распавшихся за время  , равно
, равно  , где
, где  – число нераспавшихся атомов в момент времени
– число нераспавшихся атомов в момент времени  , и мы емеем дифференциальное уравнение
, и мы емеем дифференциальное уравнение
 .
. ,
, – температура тела,
– температура тела,  – температура окружающей среды,
– температура окружающей среды,  – коэффициент остывания.
– коэффициент остывания. световой поток, падающий на поверхность на глубине
световой поток, падающий на поверхность на глубине 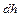 поглощенный световой поток
поглощенный световой поток 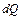 равен
равен ,
, ).
). положительных и столько же отрицательных ионов в данном объеме газа. Вследствие того, что положительные и отрицательные ионы снова соединяются между собой, количество их убывает. Принимая, что из общего количества
положительных и столько же отрицательных ионов в данном объеме газа. Вследствие того, что положительные и отрицательные ионы снова соединяются между собой, количество их убывает. Принимая, что из общего количества  положительных ионов в каждую секунду соединяется часть, пропорциональная квадрату их количества (коэффициент пропорциональности
положительных ионов в каждую секунду соединяется часть, пропорциональная квадрату их количества (коэффициент пропорциональности  зависит от природы и состояния газа), установим зависимость количества ионов
зависит от природы и состояния газа), установим зависимость количества ионов  .
. Пусть подводная лодка, находящаяся в момент времени
Пусть подводная лодка, находящаяся в момент времени  на глубине
на глубине  от поверхности моря и движущаяся с постоянной горизонтальной скоростью
от поверхности моря и движущаяся с постоянной горизонтальной скоростью 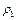 стала меньше плотности воды
стала меньше плотности воды  , невелик, то можно считать, что в момент
, невелик, то можно считать, что в момент  , где
, где  – ускорение свободного падения,
– ускорение свободного падения,  – объем подлодки. Суммарная сила, действующая на подлодку в вертикальном направлении, - разность между
– объем подлодки. Суммарная сила, действующая на подлодку в вертикальном направлении, - разность между  и весом тела
и весом тела  , а сообщаемое ею ускорение по второму закону Ньютона равно
, а сообщаемое ею ускорение по второму закону Ньютона равно .
. , характеризующая горизонтальное положение подлодки, изменяется по закону движения тела с постоянной скоростью:
, характеризующая горизонтальное положение подлодки, изменяется по закону движения тела с постоянной скоростью: .
.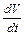 . При увеличении скорости падения с течением времени, сопротивление среды также возрастает. При малых скоростях сила сопротивления среды равна
. При увеличении скорости падения с течением времени, сопротивление среды также возрастает. При малых скоростях сила сопротивления среды равна  , где
, где  ,
, 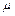 – динамическая вязкость среды,
– динамическая вязкость среды,  – радиус шарика.
– радиус шарика.  ,
,  – коэффициент лобового сопротивления,
– коэффициент лобового сопротивления,  – площадь поперечного сечения,
– площадь поперечного сечения,  – плотность среды.
– плотность среды. . Через некоторое время после начала падения движение станет равномерным, поэтому сила тяжести сравняется с силой сопротивления, т. е.
. Через некоторое время после начала падения движение станет равномерным, поэтому сила тяжести сравняется с силой сопротивления, т. е.  .
. . Проецируя это уравнение на ось, направленную вертикально вниз получим:
. Проецируя это уравнение на ось, направленную вертикально вниз получим: .
. ,
, 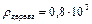 кг/м3,
кг/м3, 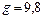 м/с2,
м/с2,  ,
,  ,
,  HC/м2,
HC/м2,  кг/м3.
кг/м3.


