
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предметная область «Социология»Содержание книги
Поиск на нашем сайте Модель «Гонка вооружений между двумя странами» [32] Математическая модель. Предполагается, что общее количество вооружений у каждой страны изменяется со временем в зависимости от трех факторов: количества оружия у противника, износа уже существующего вооружения и степени недоверия между противниками. Темпы прироста и уменьшения вооружений пропорциональны указанным факторам, т. е.
В уравнениях Модель не учитывает многие важные факторы, влияющие на динамику гонки вооружений, но, тем не менее, дает возможность проанализировать ряд существенных свойств этого процесса. Анализ наиболее прост в частном случае, когда функции
Модель «Боевые действия двух армий» [32] Математическая модель. В противоборстве могут принимать участие как регулярные армии, так и партизанские соединения. Главной характеристикой соперников в рассматриваемых моделях являются численности сторон В случае действий между регулярными частями динамика их численности определяется тремя факторами: · скоростью уменьшения состава из-за причин, непосредственно не связанных с боевыми действиями (болезни, травмы, дезертирство); · темпом потерь, обусловленных боевыми действиями противоборствующей стороны (которые в свою очередь определяются качеством ее стратегии и тактики, уровнем морального духа и профессионализмом бойцов, вооружениями и т. д.); · скоростью поступления подкреплений, которая считается некоторой заданной функцией времени. При этих предположениях для
из которой при заданных функциях Модель «Война между регулярными и партизанскими частями» [32] Математическая модель. Война между регулярными и партизанскими частями описывается другой моделью в отличии от модели боевых действий двух армий. Главное отличие в том, что нерегулярные соединения в сравнении с армейскими менее уязвимы, так как действуют скрытно, зачастую оставаясь невидимыми для соперника, вынужденного действовать неизбирательно, по площадям, занимаемым партизанами. Поэтому считается, что темп потерь партизан, проводящих свои операции в разных местах на некоторой известной территории, пропорционален не только численности армейских соединений
В уравнениях коэффициенты Модель Саймона [1] Математическая модель. Модель Саймона является формализацией некоторых постулатов теории малых групп Д. Хоманса. Эти постулаты согласно Д. Хомансу таковы: 1. Если деятельность изменяется, то взаимодействие, вообще говоря, также изменяется, и обратно. 2. Лица, которые часто взаимодействуют друг с другом, стремятся любить друг друга. 3. Если взаимодействие между членами группы часто осуществляется во внешней системе, чувство любви между членами растет, и это чувство, в свою очередь, способствует проявлению взаимодействия во внешней системе. 4. Лица, которые имеют чувство любви друг к другу, будут выражать это чувство сверх деятельности внешней системы, и эта деятельность в дальнейшем будет усиливать чувство любви. 5. Чем больше люди взаимодействуют друг с другом, тем более в некотором отношении они становятся похожими как в своей деятельности, так и в чувствах. Саймон осуществил «перевод» постулатов Хоманса в следующую математическую модель:
где Уравнение (1) – алгебраическое (структурное). В этом уравнении
2.5. Модели для самостоятельного исследования
Построить и исследовать следующие модели. 1. Модель «Вертикальный взлет ракеты» [24]. 2. Модель «Полет трехступенчатой ракеты Сатурн V». 3. Модель «Движение тела, брошенного под углом к горизонту» [24]. 4. Модель «Движение небесных тел» [24]. 5. Модель «Движение заряженных частиц» [24]. 6. Модель «Колебания математического маятника» [24, 32]. 7. Модель «Колебания математического маятника с трением в точке подвеса» [24]. 8. Модель «Вынужденные колебания маятника» [24]. 9. Моедль «Изгиб балки» [16]. 10. Модель «Теплопердача через трубу» [16]. 11. Модель «Гармонические колебания» [16]. 12. Модель «Изменение уровня жидкости в сообщающихся сосудах» [16]. 13. Модель «Межвидовая конкуренция» [24]. 14. Модель «Рост производства с учетом банковских инвестиций» [1]. 15. Модель «Колебания рыночных цен» [1]. 16. Модель «Рост выпуска продукции в условиях конкуренции» [1] 17. Модель «Выбытие фондов» [1]. 18. Модель «Затраты на военные действия» [1]. 19. Модель «Рост населения земли с учетом насыщения» [1]. 20. Модель «Поток научной информации при резком изменении внешних условий» [16].
3. Имитационное моделирование дискретных динамических систем 3.1. Программное обеспечение для моделирования дискретных динамических систем Основоположник теории систем Людвиг фон Берталанфи определял систему как комплекс взаимодействующих элементов или как совокупность элементов, находящихся в определенных отношениях друг с другом и со средой. Понятием «состояние» обычно характеризуют мгновенную «фотографию», «срез» системы, остановку в ее развитии. Иными словами, состояние - это множество существенных свойств, которыми система обладает в данный момент времени. Если система способна переходить из одного состояния в другое, то говорят, что она обладает поведением. Этим понятием пользуются, когда неизвестны закономерности переходов из одного состояния в другое. Создание модели системы позволяет предсказывать ее поведение в определенном диапазоне условий. Целью дискретного имитационного моделирования является воспроизведение взаимодействий между компонентами исследуемой системы и изучение ее поведения и функциональных возможностей. Имитация может быть статической, позволяющей исследовать поведение модели системы в определенный момент времени или динамической, позволяющей исследовать поведение в течение продолжительных периодов времени. При имитационном моделировании основными понятиями являются: «событие», «действие», «процесс». Состояние системы может меняться только в моменты совершения событий. Событие происходит в тот момент, когда принимается решение о начале или окончании действия. Процесс - это ориентированная во времени последовательность событий, которая может состоять из нескольких действий. Функционирование дискретной имитационной модели можно определить следующими способами: · определяя изменения состояния системы, происходящие в момент совершения событий; · описывая действия, в которых принимают участие элементы системы; · описывая процесс, через который проходят элементы. Эти представления лежат в основе трех альтернативных методологических подходов к построению дискретных моделей, называемых обычно событийным подходом; подходом, ориентированным на действия, и процессно-ориентированным подходом. Для дискретных имитационных систем в соответствии с тремя методологическими подходами к моделированию можно выделить три принципиально различные группы систем моделирования. 1. При событийном подходе системы моделируются путем идентификации изменений, происходящих в моменты совершения событий. Для имитации необходимо воспроизвести хронологию (календарь) событий и причины, вызывающие их появление в соответствующие моменты имитационного времени. Календарь первоначально содержит отметку только о первом событии - «прибытие». В ходе моделирования возникновение других событий - «прибытие» и «конец обслуживания» - должно быть запланировано в календаре в соответствии с логикой функционирования системы. События выполняются в упорядоченной последовательности, при этом имитационное время продвигается от одного события к другому. Рассмотрим, например, парикмахерскую с одним парикмахером. Клиенты заходят в парикмахерскую, после возможного ожидания в очереди обслуживаются и уходят. Состояние системы определяется состоянием парикмахера и числом ожидающих обслуживания клиентов. Оно остается неизменным, за исключением моментов, когда клиент прибывает в систему или покидает ее. Событийная модель в данном случае состоит из описания действий, происходящих в момент прибытия и окончания обслуживания очередного клиента, т. е. события «прибытие» и «окончание обслуживания» полностью обеспечивают воспроизведение динамики функционирования системы. К языкам имитационного моделирования, реализующим событийный подход, относятся GASP, SEAL, СИМКОМ, СИМПАК, SIMSCRIPT и другие. 2. Подход, ориентированный на действия. При использовании данного подхода, который называют также «сканированием активностей», описываются действия, в которых принимают участие элементы системы, и задаются условия, определяющие начало и окончание этих действий. События, которые начинают или завершают действие, инициируются по условиям, определенным для данного действия. Условия начала или окончания действия проверяются после очередного продвижения имитационного времени. Если заданные условия удовлетворяются, происходит соответствующее действие. Для того чтобы было выполнено каждое действие в модели, проверка (сканирование) условий производится для всего множества действий при каждом продвижении имитационного времени. Такой подход обеспечивает простую схему моделирования для решения целого ряда проблем. Он наиболее эффективен для ситуаций, в которых продолжительность действия определяется в зависимости от того, насколько состояние системы удовлетворяет заданным условиям. Примерами в этой группе могут служить системы FORSIM, CSL, ESP, AS, GSP и другие. 3. Процессно-ориентированный подход. Многие имитационные модели содержат последовательности компонентов, которые возникают в них по определенной схеме, например, очередь, в которой клиенты ожидают обслуживания. Логика возникновения компонентов по требуемой схеме может быть задана в одном операторе. Имитационный язык затем транслирует такие операторы в соответствующую последовательность событий, происходящих с компонентами модели. Например, для описания процесса в модели банка может быть использован следующий набор операторов. 1) создавать прибывающих клиентов через каждые Т единиц времени, 2) ожидать освобождения кассира; 3) продвинуть время на время обслуживания; 4) освободить кассира; 5) удалить клиента. Первый оператор генерирует прибывающих в систему клиентов через каждые Т единиц модельного (имитационного) времени, причем величина Т может быть постоянной или случайной. Оператор «ожидать» определяет, что клиент ожидает до тех пор, пока кассир освободится. Этот оператор аналогичен понятию действия по условию, применяемому в подходе сканирования активностей. Оператор «продвинуть время» моделирует тот период времени, в течение которого клиент обслуживается кассиром. Этот тип оператора аналогичен оператору планирования в событийном подходе. Он помещает в календарь событий метку о том, что обслуживание клиента будет закончено в момент, равный текущему модельному времени плюс время обслуживания. После завершения обслуживания клиент освобождает кассира и покидает систему. Процессно-ориентированный подход сочетает в себе черты событийного и ориентированного на действия подходов. Он обеспечивает описание прохождения компонентов через процесс, содержащий ресурсы. Достоинством этого подхода является его простота, так как определяемая операторами логика событий заложена в самом имитационном языке. В то же время из-за ограниченности набора стандартных операторов языка этот подход является менее гибким, чем событийный. Примерами в этой группе являются такие системы как SIMULA, GPSS, SOL, SPL и другие. К числу общих особенностей имитационных систем следует отнести способность генерировать случайные возмущения с требуемыми вероятностными характеристиками, возможность управления модельным временем, способность накапливать и обрабатывать статистические данные, получаемые в процессе моделирования, возможность воспроизводить временные и прочие зависимости между компонентами моделируемой системы.
3.2. Система имитационного моделирования GPSS GPSS (General Purpose Simulating System - общецелевая система моделирования) разработана специалистами фирмы IBM для моделирования сложных дискретных систем, которые могут быть формализованы, например, в виде систем массового обслуживания. Объекты GPSS подразделяются на 7 категорий и позволяют, с одной стороны, описывать их взаимодействие сравнительно простыми наборами операций, а с другой - достаточно наглядно представить процесс функционирования исследуемой системы. Основными типами объектов являются транзакты и блоки, относящиеся, соответственно, к динамической и операционной категориям. Практически все изменения состояний модели системы происходят в результате обработки транзактов блоками в соответствии со своими функциями. С блоками непосредственно связаны команды, управляющие процессом моделирования и редактирования результатов моделирования. Работа GPSS-модели заключается в перемещении транзактов от блоков к блокам.
В самом начале моделирования GPSS-модели нет ни одного транзакта. В процессе моделирования транзакты входят в модель в определенные моменты времени в соответствии с теми логическими потребностями, которые возникают в моделируемой системе. Подобным же образом транзакты покидают модель в определенные моменты времени в зависимости от специфики моделирования. В общем случае в модели существует большое число транзактов, однако в один момент времени двигается только один транзакт. Если транзакт начал свое движение, он перемещается от блока к блоку по пути, предписанному блок-схемой. Каждый блок можно рассматривать как некоторую точку, в которой происходит обращение к подпрограмме. В тот момент, когда транзакт входит в блок, на исполнение вызывается соответствующая подпрограмма, и далее транзакт (в общем случае) пытается войти в следующий блок. Такое продвижение транзакта продолжается до тех пор, пока не произойдет одно из следующих возможных событий: 1) транзакт входит в блок, функцией которого является задержка транзакта на некоторое определенное моделью время; 2) транзакт входит в некоторый блок, функцией которого является удаление транзакта из модели; 3) транзакт «пытается» войти в следующий блок в соответствии с предписанной блок-схемой логикой, однако, блок «отказывается» принять этот транзакт. В этом случае транзакт остается в том блоке, в котором он в настоящее время находится. Позднее он будет повторять свою попытку войти в следующий блок. Когда условия в модели изменятся, одна из таких попыток может оказаться успешной. После этого транзакт сможет продолжать свое перемещение в модели. Если возникло одно из описанных условий, транзакт остается на месте, и начинается перемещение в модели другого транзакта. Операционные объекты, т. е. блоки, задают логику функционирования модели системы и определяют пути движения транзактов между объектами аппаратной категории. Объекты аппаратной категории - это абстрактные элементы (устройства, памяти и логические ключи), на которые может быть разделено оборудование реальной системы. Воздействуя на эти объекты, транзакты могут изменять их состояние и влиять на движение других транзактов. Объекты вычислительной категории служат для описания таких ситуаций в процессе моделирования, когда связи между компонентами системы наиболее просто и компактно выражаются в виде математических (аналитических и логических) соотношений. Для этих целей предусмотрены арифметические и булевские переменные и функции. К статистическим объектам относятся очереди и таблицы, вводимые для оценки характеристик поведения системы. Движение транзакта может быть разбито на цепь элементарных событий, происходящих в определенные моменты времени. Основной задачей симулятора GPSS является определение моментов наступления этих событий, расположение их в определенной временной последовательности и выполнение соответствующих действий при наступлении каждого события. Чтобы обеспечить правильную последовательность обработки событий во времени, в симуляторе организованы «системные часы» (таймер), хранящие значения абсолютного времени модели. Все отрезки времени описываются целыми числами, поэтому при составлении модели необходимо привести все временные параметры и характеристики системы к единому временному масштабу, т е. задать значение условной единицы времени. Каждому объекту соответствуют атрибуты, описывающие его состояние в данный момент времени. Значения атрибутов могут быть арифметическими или логическими. Атрибуты, на которые можно ссылаться в процессе моделирования, называются стандартными числовыми атрибутами (СЧА). Перечень СЧА для различных типов объектов приведен в приложении 1.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 746; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ,
, .
. ,
,  – объемы вооружений, коэффициенты
– объемы вооружений, коэффициенты  ,
,  ,
,  ,
,  характеризуют скорости наращивания и «старения» вооружений (аналог процесса амортизации производственных мощностей в моделях экономики), функции
характеризуют скорости наращивания и «старения» вооружений (аналог процесса амортизации производственных мощностей в моделях экономики), функции  ,
,  описывают уровень взаимной настороженности (недоверия) конкурентов, который считается не зависящим от количества вооружений, а определяется другими причинами.
описывают уровень взаимной настороженности (недоверия) конкурентов, который считается не зависящим от количества вооружений, а определяется другими причинами.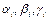 ,
,  , не зависят от времени:
, не зависят от времени: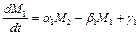 ,
, .
. и
и  . Если в какой-то момент времени одна из численностей обращается в нуль, то данная сторона считается потерпевшей поражение (притом, что в этот момент численность другой стороны положительна).
. Если в какой-то момент времени одна из численностей обращается в нуль, то данная сторона считается потерпевшей поражение (притом, что в этот момент численность другой стороны положительна). ,
, 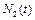 получаем систему уравнений
получаем систему уравнений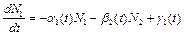 ,
, ,
, ,
,  однозначно определяется решение в любой момент времени
однозначно определяется решение в любой момент времени  . В уравнениях коэффициенты
. В уравнениях коэффициенты  характеризуют скорости потерь в силу обычных (не боевых) причин,
характеризуют скорости потерь в силу обычных (не боевых) причин,  – темпы потерь из-за действий соперника,
– темпы потерь из-за действий соперника,  – скорости поступления подкреплений.
– скорости поступления подкреплений. . В результате модель становится нелинейной:
. В результате модель становится нелинейной: ,
, , (1)
, (1) , (2)
, (2) , (3)
, (3) – интенсивность взаимодействия среди членов группы;
– интенсивность взаимодействия среди членов группы;  – степень дружелюбия среди членов группы;
– степень дружелюбия среди членов группы;  – уровень деятельности, выполненной группой;
– уровень деятельности, выполненной группой;  – объем внешненавязанной деятельности («внешняя система»).
– объем внешненавязанной деятельности («внешняя система»). выражается как функция
выражается как функция  и
и  . Из этого уравнения вытекают постулаты Хоманса о взаимосвязи между степенью дружелюбия среди членов группы
. Из этого уравнения вытекают постулаты Хоманса о взаимосвязи между степенью дружелюбия среди членов группы  , уровнем деятельности, выполненной группой
, уровнем деятельности, выполненной группой  и интенсивностью взаимодействия среди членов группы
и интенсивностью взаимодействия среди членов группы  . Для того чтобы получить постулаты Хоманса о связи этих факторов с объемом внешней деятельности
. Для того чтобы получить постулаты Хоманса о связи этих факторов с объемом внешней деятельности  , подставим уравнение (1) в (2). Получим систему двух дифференциальных уравнений (2) и (3). С четырьмя переменными
, подставим уравнение (1) в (2). Получим систему двух дифференциальных уравнений (2) и (3). С четырьмя переменными 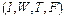 и пятью свободными параметрами
и пятью свободными параметрами  .
.


