
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предметные области «Биология» и «Экология»Содержание книги
Поиск на нашем сайте
Модель «Динамика популяции» [16] Математическая модель. Пусть в момент Модель «Внутривидовая конкуренция» [24] Математическая модель. Обозначим за N численность популяции. Скорость роста можно обозначить как, тогда средняя скорость увеличения численности в расчёте на одну особь определяется величиной Без учёта внутривидовой конкуренции получаем Теперь попробуем учесть внутривидовую конкуренцию. Когда численность популяции близка к нулю, скорость роста определяется
Это уравнение известно под названием «логистического», где Модель «Хищник-жертва» с логистической поправкой [24] Математическая модель. Модель конкурирующих видов – это модель Холлинга-Тэннера. Скорость роста популяции жертв Скорость роста популяции хищников
где Модель «Размножение бактерий» [16] Математическая модель. Пусть Дифференциальное уравнение, описывающее закон размножения бактерий имеет следующий вид: Модель «Клеточная популяция» [16] Математическая модель Популяция разбита на две группы клеток: молодые и старые. Будем считать, что клетки первой группы интенсивно растут, но не достигли физиологической зрелости и неспособны делиться. Члены второй группы способны к делению. Требуется определить развитие численности старых и молодых клеток при изменении их числа особей, скорости протока. Будем считать, что клетки первой группы интенсивно растут, но не достигли физиологической зрелости и неспособны делиться. Члены второй группы способны к делению. Процесс деления может быть задержан при помощи различных ингибиторов. Уравнения для численностей молодых (
где Модель «Загрязнение воды» [25] Математическая модель. Биохимическая потребность кислорода является мерой концентрации органических загрязнений воды и определяется количеством кислорода на единицу объема воды, необходимого для разложения загрязнений (мг/л воды). Обозначим её
При отсутствии отходов концентрация кислорода в воде равна равновесной концентрации, являющейся функцией температуры. При наличии отходов концентрация кислорода понижается на величину
Модель «Распространение эпидемий» [32] Математическая модель. Пусть заболевшие от общества не изолируются. В начальный момент времени Количество здоровых людей определяется формулой Введем Таким образом,
Предметная область «Химия»
Модель «Химическая реакция» [16] Математическая модель. Если 1) в случае перехода вещества
где 2) в случае перехода двух веществ
где Модель «Закон растворения» [16] Математическая модель. В основе теории растворения лежит гипотеза о том, что если температура Дифференциальное уравнение, описывающее закон растворения имеет следующий вид:
где Модель «Очищение газа» [16] Математическая модель. Для очистки газа от некоторой газообразной примеси его пропускает через скруббер (сосуд, содержащий тот или иной поглотитель). Количество газообразной примеси, поглощаемое тонким слоем поглотителя при установившемся режиме аппарата, пропорционально концентрации примеси, а также толщине и площади поперечного сечения слоя. Скруббер имеет форму конуса с радиусом основания Обозначим концентрацию примеси через Таким образом,
где
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 483; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.42.122 (0.008 с.) |

 биомасса некоторой популяции равна
биомасса некоторой популяции равна 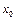 . Скорость увеличения биомассы пропорциональна самой биомассе. Коэффициент пропорциональности
. Скорость увеличения биомассы пропорциональна самой биомассе. Коэффициент пропорциональности  называется коэффициентом размножения. Однако с ростом биомассы условия существования организмов ухудшаются пропорционально квадрату биомассы. Это явление называется самоотравлением, а соответствующий коэффициент пропорциональности
называется коэффициентом размножения. Однако с ростом биомассы условия существования организмов ухудшаются пропорционально квадрату биомассы. Это явление называется самоотравлением, а соответствующий коэффициент пропорциональности  – коэффициентом самоотравления. Изменение биомассы определяется формулой:
– коэффициентом самоотравления. Изменение биомассы определяется формулой: 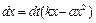 или
или  .
.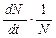 .
.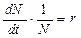 или
или  , где
, где  – мгновенная удельная скорость роста численности, то есть приращение численности за единицу времени в пересчёте на одну особь.
– мгновенная удельная скорость роста численности, то есть приращение численности за единицу времени в пересчёте на одну особь. достигается значение
достигается значение 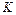 (предельная численность популяции), скорость роста популяции снижается до нуля. Учитывая всё это, получаем
(предельная численность популяции), скорость роста популяции снижается до нуля. Учитывая всё это, получаем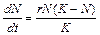
 – скорость роста популяции,
– скорость роста популяции,  в этой модели равна сумме трех величин: скорости размножения в отсутствие хищников
в этой модели равна сумме трех величин: скорости размножения в отсутствие хищников  ; влиянию межвидовой конкуренции за пищу при ограниченных ресурсах (для случая конкурирующих производителей – это влияние ограниченных сырьевых ресурсов)
; влиянию межвидовой конкуренции за пищу при ограниченных ресурсах (для случая конкурирующих производителей – это влияние ограниченных сырьевых ресурсов)  ; влиянию хищников, в предположении, что хищник перестает убивать, когда насыщается
; влиянию хищников, в предположении, что хищник перестает убивать, когда насыщается  .
. строится так же, как в модели Вольтера-Лотка, в предположении, что жертвы встречаются редко. Если для поддержания жизни одного хищника нужно
строится так же, как в модели Вольтера-Лотка, в предположении, что жертвы встречаются редко. Если для поддержания жизни одного хищника нужно  жертв, то популяция из
жертв, то популяция из  жертв сможет обеспечить пищей
жертв сможет обеспечить пищей  хищников. Модель роста популяции хищников, в которой их число не может превысить эту критическую величину, имеет вид
хищников. Модель роста популяции хищников, в которой их число не может превысить эту критическую величину, имеет вид  . Таким образом, имеем модель Холлинга-Тэннера:
. Таким образом, имеем модель Холлинга-Тэннера:
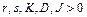 .
. – количество всех бактерий в момент времени
– количество всех бактерий в момент времени  , тогда
, тогда  – скорость их размножения.
– скорость их размножения. , где
, где  – заданная постоянная, зависящая от вида бактерий и внешних условий.
– заданная постоянная, зависящая от вида бактерий и внешних условий.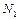 ) и старых (
) и старых ( ) клеток имеют вид:
) клеток имеют вид: ,
, – среднее время созревания «молодой» клетки,
– среднее время созревания «молодой» клетки,  – среднее время пребывания «старой» клетки в детородном периоде,
– среднее время пребывания «старой» клетки в детородном периоде,  – скорость протока через хемостат.
– скорость протока через хемостат.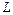 . Скорость разложения отходов, загрязняющих воду, определяется формулой:
. Скорость разложения отходов, загрязняющих воду, определяется формулой: , где
, где 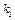 – постоянная отбора кислорода.
– постоянная отбора кислорода. . Величина
. Величина 
 в группу
в группу  – количество заболевших людей, получим
– количество заболевших людей, получим  .
.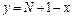 .
. заболеют
заболеют  людей:
людей: 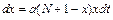 , где
, где  - количество встреч больных со здоровыми.
- количество встреч больных со здоровыми.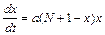 .
.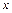 – количество вещества
– количество вещества  , в которое переходит каждое из двух веществ
, в которое переходит каждое из двух веществ  и
и 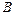 , то при постоянстве температуры и соблюдении некоторых других условий полагают, что скорость реакции
, то при постоянстве температуры и соблюдении некоторых других условий полагают, что скорость реакции  ,
, ;
; ,
, – начальные количества веществ
– начальные количества веществ  .
. насыщенного какой – либо солью растворителя получает приращение
насыщенного какой – либо солью растворителя получает приращение  , пропорциональное
, пропорциональное 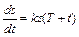 ,
, и высотой
и высотой  . Газ поступает через вершину конуса. Зависимость концентрации газообразной примеси в скруббере определяется как функция расстояния слоя от вершины конуса. Учитывается, что концентрация примеси в поступающем газе равна
. Газ поступает через вершину конуса. Зависимость концентрации газообразной примеси в скруббере определяется как функция расстояния слоя от вершины конуса. Учитывается, что концентрация примеси в поступающем газе равна 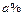 , а в выходящем
, а в выходящем  .
.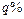 , а расстояние слоя от вершины конуса через
, а расстояние слоя от вершины конуса через  .
.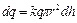 ,
, , так что
, так что .
.


