
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование пространственно-временных явлений и преобразователейСодержание книги
Поиск на нашем сайте
2.1 Цель работы
Изучение индукционного метода преобразования пространственной физической величины (углового перемещения) в фазу выходного сигнала. Определение диапазона преобразования и влияния формы вращающегося магнитного поля на функцию преобразования (ФП). Изучение времяимпульсного метода преобразования фазы в аналоговый и цифровой сигналы.
2.2 Теоретическая часть
2.2.1 Индукционные фазовые преобразователи перемещения.
Для построения преобразователей перемещения в фазу переменного напряжения (тока) используются обычно два метода; а) параметрический; б) индукционный с вращающимся магнитным полем. В параметрических преобразователях измеряемое перемещение изменяет комплексное сопротивление цепи переменного тока. Для построения преобразователей перемещения с фазовым (фазовращательным) выходом чаще используется вращающееся магнитное поле, так же как и в асинхронных (синхронных) электрических двигателях. Фазовращатели представляют собой электрическую машину переменного тока и состоят из статора и ротора. Чаще статор имеет несколько симметричных обмоток, сдвинутых в пространстве, к которым подводятся напряжения, сдвинутые соответственно по фазе, равные пространственному сдвигу между катушками. Обычно используются двухфазное или трехфазное питание, следовательно, статорные обмотки должны иметь сдвиг в пространстве соответственно 90° или 120°. Рассмотрим работу двухфазного фазовращателя, электрическая схема которого приведена на рис. 1
Рис. 1. Двухфазный фазовращатель
Статорные обмотки
Рис. 2. Векторная диаграмма магнитного поля
Получение вращающегося магнитного поля можно пояснить векторной диаграммой (рис. 2), где ''+1'', ''+ j '' положительное направление вещественной и мнимой оси, совпадающее с магнитными осями катушек Напряжения
В момент времени
Тогда модуль суммарного вектора:
а угол сдвига
Следовательно, при любом значении Направление вращения магнитного поля можно изменить на противоположное, переключив питающие напряжения. Как уже было сказано, вращающееся магнитное поле индуктирует в обмотках ротора ЭДС, фаза которой определяется положением ротора – a. При равенстве напряжений При несоблюдении указанных условий получается эллиптическое поле непостоянной угловой скоростью, приводящее к погрешности. Преимущества рассматриваемого метода перед параметрическим определяются тем, что имеется линейная зависимость между углом поворота ротора и углом сдвига фазы практически в пределах 0¸360°. Одновременное изменение частот и амплитуд питающих напряжений не влияет на фазовый сдвиг. Для построения преобразователя с фазовым выходом для описанного случая используют синусно-косинусные вращающиеся трансформаторы. При этом напряжения Часто для получения вращающегося магнитного поля используется трёхфазный ток, следовательно, необходимо иметь систему из трёх катушек (обычно на статоре), сдвинутых в пространстве под углом 120° друг к другу. Вращающееся магнитное поле так же, как и при двухфазном питании обмоток, наводит в роторной обмотке ЭДС с постоянной амплитудой и фазой, определяемой угловым положением ротора. При питании трёхфазным током преобразователи перемещения с фазовым выходом можно построить на основе сельсинов, у которых статорная обмотка имеет трёхфазную обмотку. В отличие от асинхронных (синхронных) двигателей обмотки сельсинов и вращающихся трансформаторов выполняются с большей симметрией.
2.2.2 Измерение фазы выходного напряжения
Фазу выходного напряжения описанных преобразователей определяют относительно фазы опорного напряжения, за которое может быть принято напряжение любой статорной катушки, при этом нулевое положение ротора определяется совпадением магнитной оси обмотки ротора и той катушки, напряжение которой принято за опорное (рис.1). Измерение фазы обычно производится фазометрами, которые бывают различных типов. Большую точность измерения фазы можно получить при использовании времяимпульсного метода преобразования, который заключается в получении импульсов с частотой питающего напряжения, но длительностью, пропорциональной фазе выходного напряжения. Указанный метод позволяет получить аналоговый или цифровой сигнал. Последовательность преобразований опорного и выходного напряжений показана на (рис. 3). Сдвиг фазы выходного напряжения j может быть легко определён сравнением наиболее характерных одноименных точек кривых (рис. 3а), например, нулевых моментов. Для этого синусоидальные напряжения преобразуют в прямоугольные той же частоты (рис. 3б), тогда время сдвига между прямоугольными импульсами:
и изменяется в зависимости от изменения фазы в пределах периода сравниваемых напряжений – Для перехода от времени сдвига Триггер является двоичным элементом памяти, т.е. имеет два устойчивых состояния (1 и 0) с двумя входами Процесс повторится при поступлении ‘1’ на вход Если на входы Следовательно, если продифференцировать прямоугольные напряжения
Рис. 3. Последовательность преобразования угла сдвига фаз
Воспользовавшись уравнением (2.2.7), имеем:
Большую точность можно получить при цифровом методе измерения времени
где Так как в общем случае в измеряемый интервал
Рис. 5. Преобразование временного интервалы в импульсы
Таким образом, счетчик отсчитает целую часть
Эта величина является случайной, а максимальное значение абсолютной погрешности счета, очевидно, равно Уменьшить эту погрешность можно уменьшая период следования Для считывания Если время измерения
где
В процессе работы из-за нестабильности При максимальной абсолютной погрешности измерения времени импульса
где Кроме рассмотренной методической погрешности от дискретности, суммарная погрешность определится следующими факторами: а) неравенством амплитуд линейных напряжений; б) изменением фазы между напряжениями; в) не синусоидальностью питающих напряжений; г) неточностью симметрирования обмоток; д) технологическими. Следовательно, у фазовых преобразователей суммарная погрешность зависит от многих факторов. При исследовании индукционного фазовращателя следует определить суммарную погрешность и выделить максимальную погрешность от дискретности.
2.3 Описание лабораторной установки
Лабораторная установка (рис. 6) состоит из лабораторного пульта и измерительных приборов: электронного вольтметра; двухлучевого осциллографа; цифрового частотомера и генератора Лабораторный пульт позволяет исследовать фазовый преобразователь угла поворота, построенный на базе сельсина, обмотки которого показаны на пульте (рис. 6). Угол поворота ротора с обмоткой
Сопротивление R позволяет изменять форму вращающегося магнитного поля в статоре. Опорное напряжение
2.4 Порядок выполнения работы
1. Прежде чем приступить к исследованию преобразователя, необходимо изучить принцип работы преобразователя, времяимпульсный метод преобразования фазы, ознакомиться с лабораторной установкой и записать данные измерительных приборов в бланке отчета. 2. Включить измерительные приборы (осциллограф, вольтметр, генератор сигналов, частотомер). Зарисовать схему установки. 3. Определить последовательно форму выходного и опорного напряжения в точках 1¸6 и зарисовать их в отчете. Для этого включить установку (тумблер В1) и последовательно включать входы двухлучевого осциллографа к контрольным точкам (1¸6). Замерить частоты
ВНИМАНИЕ! Не допускается замыкание контрольных точек с выводами ‘ 4. Экспериментальное определение статической характеристики преобразователя 5. Экспериментальное определение статической характеристики преобразователя для некругового вращающегося магнитного поля. Установить линейное напряжение 6. Экспериментальное определение влияния частоты задающего генератора –
где
Провести аналогичные измерения при 7. Выключить измерительные приборы, лабораторный стенд. Результаты измерений занести в таблицу.
8. По данным измерения для кругового и эллиптического вращающихся магнитных полей вычислить для каждой точки
и является линейной. При определении суммарной погрешности округлять 9. По данным измерений и вычислений построить на миллиметровой бумаге графики Оформить отчет, сделать выводы по проведенной работе и ответить на контрольные вопросы.
2.5 Требования к отчету
Отчет должен содержать: 1. цель работы; 2. схему установки; 3. результаты измерений, занесенные в таблицу; 4. графики, построенные по результатам измерений и вычислений; 5. выводы.
2.6 Контрольные вопросы
1. Какими причинами вызвана нелинейность построенных графиков? 2. Каким образом можно уменьшить погрешность от дискретности? 3. Влияет ли на суммарную погрешность время измерения количества импульсов? 4. Почему искажение sin-ой формы питающих напряжений вызывает погрешность преобразования угла? 5. Каковы причины возникновения погрешностей на каждом этапе преобразования перемещения в цифровой сигнал, в напряжение? 6. Почему диапазон измерения не равен 360°? Лабораторная работа № 3
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.241.87 (0.009 с.) |


 и
и  одинаковы, а их магнитные оси взаимноперпендикулярны. К ним подаются два переменных напряжения, но с одинаковой амплитудой и частотой, сдвинутые по фазе на 90°, при этом образуется вращающееся магнитное поле, индуктирующее в обмотке ротора W ЭДС, фаза которого линейно зависит от углового положения ротора.
одинаковы, а их магнитные оси взаимноперпендикулярны. К ним подаются два переменных напряжения, но с одинаковой амплитудой и частотой, сдвинутые по фазе на 90°, при этом образуется вращающееся магнитное поле, индуктирующее в обмотке ротора W ЭДС, фаза которого линейно зависит от углового положения ротора.
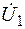 и
и 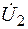 создают соответственно потоки:
создают соответственно потоки: (2.2.1)
(2.2.1) (2.2.2)
(2.2.2) поток
поток  и совпадает с вещественной осью (рис.2),
и совпадает с вещественной осью (рис.2), 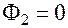 . При
. При  имеем соответственно
имеем соответственно (2.2.3)
(2.2.3) (2.2.4)
(2.2.4) , (2.2.5)
, (2.2.5) . (2.2.6)
. (2.2.6)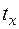 модуль суммарного потока остается постоянным, а угол φ пропорционален времени
модуль суммарного потока остается постоянным, а угол φ пропорционален времени  и угла сдвига фаз между ними, равным 90°, вращающееся магнитное поле будет круговым с постоянной угловой скоростью – w, следовательно, имеем равенство угла поворота и фазы выходного напряжения
и угла сдвига фаз между ними, равным 90°, вращающееся магнитное поле будет круговым с постоянной угловой скоростью – w, следовательно, имеем равенство угла поворота и фазы выходного напряжения  .
.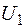 и
и 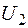 (рис.1) подаются соответственно на синусную и косинусную обмотки, расположенные в пространстве под углом 90° друг к другу.
(рис.1) подаются соответственно на синусную и косинусную обмотки, расположенные в пространстве под углом 90° друг к другу.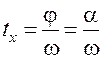 ,
,  (2.2.7)
(2.2.7)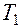 .
. к импульсу прямоугольного напряжения с длительностью
к импульсу прямоугольного напряжения с длительностью 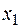 и
и  и двумя выходами
и двумя выходами 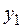 (прямой) и
(прямой) и  (инверсный). При подаче импульса напряжения на вход
(инверсный). При подаче импульса напряжения на вход  .
. и
и  и подать импульсы, соответствующие производным их передних фронтов (рис. 3в), на входы
и подать импульсы, соответствующие производным их передних фронтов (рис. 3в), на входы  , получим аналоговый сигнал, пропорциональный
, получим аналоговый сигнал, пропорциональный 
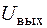
 Рис. 4. Схема работы триггера
Рис. 4. Схема работы триггера (2.2.8)
(2.2.8) (2.2.9)
(2.2.9) (рис.5) равную числу прошедших к счетчику импульсов (метод последовательного счета). В этом случае выходной величиной является количество импульсов
(рис.5) равную числу прошедших к счетчику импульсов (метод последовательного счета). В этом случае выходной величиной является количество импульсов  , (2.2.10)
, (2.2.10)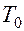 – период следования квантующих импульсов.
– период следования квантующих импульсов.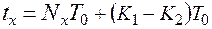 (2.2.11)
(2.2.11)
 , а дробная часть, в которой
, а дробная часть, в которой 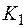 и
и  могут принимать значения
могут принимать значения  при
при  или
или  при
при  и все значения между 0 и 1 является абсолютной погрешностью:
и все значения между 0 и 1 является абсолютной погрешностью: (2.2.12)
(2.2.12) (при
(при  , но здесь существует предел, накладываемый допустимой без ошибок скоростью счета современных счетчиков.
, но здесь существует предел, накладываемый допустимой без ошибок скоростью счета современных счетчиков. , необходимо определить
, необходимо определить  (2.2.13)
(2.2.13) – частота опорного напряжения;
– частота опорного напряжения;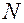 – показания частотомера при времени измерения
– показания частотомера при времени измерения  сек, т.к. при измерении частоты независимо от выставленного времени измерения оно приводится к 1 с.
сек, т.к. при измерении частоты независимо от выставленного времени измерения оно приводится к 1 с. ,
,  , а также из-за случайного характера величин
, а также из-за случайного характера величин  можно определить погрешность измерения фазы (угла поворота) из уравнения (5.2.9), т.е. при
можно определить погрешность измерения фазы (угла поворота) из уравнения (5.2.9), т.е. при  (2.2.14)
(2.2.14) – частота квантующего генератора.
– частота квантующего генератора. .
.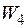 задается и измеряется угломером – У с ценой деления 3°. Статорные обмотки (
задается и измеряется угломером – У с ценой деления 3°. Статорные обмотки ( ) питаются трехфазным синусоидальным напряжением – 36 В, 400 Гц, которые включаются тумблером В1. Гнезда статорных обмоток (а, б, в) служат для измерения линейных напряжений на обмотках.
) питаются трехфазным синусоидальным напряжением – 36 В, 400 Гц, которые включаются тумблером В1. Гнезда статорных обмоток (а, б, в) служат для измерения линейных напряжений на обмотках.

 и выходное
и выходное  ). Тумблер В2 включает напряжение 220 В к гнездам ~ 220 В, к которым подключаются измерительные приборы.
). Тумблер В2 включает напряжение 220 В к гнездам ~ 220 В, к которым подключаются измерительные приборы. и
и  .
.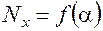 при круговом вращающемся магнитном поле. Проверить одинаковость линейных напряжений на статорных обмотках сельсина. Цифровой частотомер подключается к выходу логического элемента ‘И’ (контрольная точка 7), к контрольной точке 6 подключается внешний генератор
при круговом вращающемся магнитном поле. Проверить одинаковость линейных напряжений на статорных обмотках сельсина. Цифровой частотомер подключается к выходу логического элемента ‘И’ (контрольная точка 7), к контрольной точке 6 подключается внешний генератор  на частотомере 1 с, частоту
на частотомере 1 с, частоту  до
до  1. При нарушении линейной зависимости количество измеряемых точек в нелинейной области необходимо увеличить для более точного определения характера нелинейности.
1. При нарушении линейной зависимости количество измеряемых точек в нелинейной области необходимо увеличить для более точного определения характера нелинейности.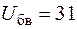 В переменным сопротивлением R и выполнить последовательно работу по пункту 4.4.
В переменным сопротивлением R и выполнить последовательно работу по пункту 4.4.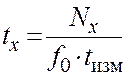 , (2.4.1)
, (2.4.1) – частота генератора;
– частота генератора;  1 с.
1 с.
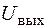 , В
, В
 – абсолютную суммарную погрешность. Номинальная функция преобразования определяется уравнениями (2.2.7) и (2.2.10)
– абсолютную суммарную погрешность. Номинальная функция преобразования определяется уравнениями (2.2.7) и (2.2.10) (2.4.2)
(2.4.2) до целого не следует.
до целого не следует. ,
,  ,
,  для обеих форм вращающегося магнитного поля, а также
для обеих форм вращающегося магнитного поля, а также  ,
,  .
.


