
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициента вязкости воздуха, средней длины свободного пробега и эффективного диаметра молекулСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оборудование: аспиратор, манометр, мензурка, секундомер. Теоретическое введение Молекулярно-кинетическая теория позволила получить формулы, связывающие макроскопические параметры газа (давление, объем, температура) с его микроскопическими параметрами (размеры и масса молекулы, ее скорость, средняя длина свободного пробега молекул). Пользуясь этими формулами на основании измеренных параметров газа можно найти его микроскопические параметры. Для нахождения средней длины свободного пробега можно воспользоваться формулой, выражающей зависимость коэффициента внутреннего трения газа η отλ и υ:
где: ρ - плотность газа, υ - средняя арифметическая скорость молекул газа равна:
здесь R= 8,31 Дж/моль∙К газовая постоянная, Т - абсолютная температура газа, М - молярная масса газа. Плотность ρ газа можно найти из уравнения Клапейрона-Менделеева.
здесь: Р- давление газа при данных условиях. Коэффициент вязкости можно определить, пользуясь законом Пуазейля. Исходя из которого коэффициент вязкости газа η зависит от параметров капиллярной трубки, через которую проходит газ, и разности давлений ΔP, поддерживаемой на концах этой трубки, т.е.:
где: r - радиус, L - длина трубки, V - объем газа, проходящего через трубку за время τ, ΔP - разность давлений на концах трубки. Подставляя выражения (4),(3) и (2) в формулу (1а), получим
где:
некоторая постоянная Эффективный диаметр молекулы можно определить из формулы, выражающей зависимость средней длины свободного пробега молекулы от концентрации молекул n и эффективного диаметра молекулы dэф
По основному уравнению молекулярно-кинетической теории газов
где:Р - давление газа (атмосферное давление); n - концентрация молекул воздуха; k=1,38∙10-23 Дж/K - постоянная Больцмана. Из формул (7),(8) получаем:
Для проведения измерения собираем установку состоящую из аспиратора, из него начнет выливаться вода, давление в нем понижается, через капилляр и осушительный фильтр в него засасывается воздух. Вследствие внутреннего трения, давление на концах не одинаково, что фиксируем манометр. Объем прошедшего через капилляр воздух за время t равен объему вылившейся из аспиратора воды, которой измеряется мензуркой.
Порядок выполнения работы 1. Наполняют баллон аспиратора водой. Осторожно открывают кран аспиратора так, чтобы вода из него текла тонкой струей, давление в нем понижается, через капилляр и осушительный фильтр в него засасывается воздух. Через некоторое время установится стационарное течение и манометр покажет некоторую постоянную разность на концах трубки. Записывают показание манометра в таблицу и определяют разность делений:
здесь: ρжид - плотность жидкости в манометре, q- ускорение свободного падения, (h2+ h1) - разность высот столбов жидкости в манометре. 2. Подставляют под струю мензурку и замеряют время t с помощью секундомера, в течение которого вытекает объем жидкости 50 - 100 см3. Объем прошедшего через капилляр воздуха за это время равен объему вылившейся из аспиратора воды. 3. Опыт повторяют еще два раза при различных истечениях воды. Результаты заносят в таблицу.
4. По формулам (5) и (4) рассчитывают λ и η. По формуле (9) определяют dэф. 5. Полученные результаты сравнивают с табличными значениями.
Таблица измерений
Контрольные вопросы 1. Основные положения МКТ и их опытное обоснование. 2. Основное уравнение МКТ газов. 3. Скорость молекул идеального газа. 4. Средняя длина свободного пробега молекул. 5. Внутреннее трение (вязкость) в газах. Коэффициент внутреннего трения. 6. Закон Пуазейля.
ЛАБОРАТОРНАЯ РАБОТА ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ВОЗДУХА МЕТОДОМ АДИАБАТИЧЕСКОГО СЖАТИЯ И РАСШИРЕНИЯ Оборудование: установка Клемана-Дезорма. Теоретическое введение Внутренняя энергия одного моля идеального газа может быть выражена уравнением:
где: R - универсальная газовая постоянная, T - абсолютная температура, Числом степеней свободы твердого тела называют число независимых координат, с помощью которых можно полностью описать его положение в пространстве. В общем случае молекула газа, рассматриваемая в виде жестко связанных атомов, может перемещаться в пространстве совершенно произвольно, т.е. участвовать в шести одновременных независимых движениях (рисунок 1) трех вращательных вокруг трех взаимно перпендикулярных осей ά, β, γ, проходящих через центр тяжести молекулы, и трех поступательных движений вдоль трех осей прямоугольной системы координат x, y, z. Таким образом в общем случае молекула газа может иметь шесть степеней свободы: три поступательных и три вращательных. Однако молекулы содержат различное число атомов, что и отражается на общем числе степеней свободы.
сматривается в виде материальной
кой точки определяется тремя коор- динатами, изменяет своего положения в прост- y Рисунок 1 ранстве. Следовательно, частица одноатомного газа имеет три поступательные степени свободы. Двухатомную молекулу можно представить в виде двух жестко связанных между собой атомов (рисунок 3а). Такая молекула будет иметь три поступательные степени свободы и две вращательные вокруг двух осей β, γ перпендикулярных к линии связи между атомами. При вращении вокруг оси α совпадающей с линией связи, двухатомная молекула не меняет своего положения в пространстве. Таким образом двухатомная молекула имеет пять степеней свободы: три поступательных и две вращательных. В трехатомной молекуле все атомы жестко связаны между собой (рисунок 3б). Такая молекула будет иметь шесть степеней свободы: три поступательных и три вращательных. Такое же число степеней свободы будет иметь и все молекулы с числом атомов больше трех. После этого отступления возвратимся вновь к рассматриваемому вопросу о внутренней энергии газа. Приращение внутренней энергии газа ΔЕ при изменении его температуры на ∆Т в соответствии с равенством (1) примет вид:
Если идеальный газ нагревается при постоянном объеме, то вся подведенная теплота затрачивается на увеличение его внутренней энергии. Отношение приращения внутренней энергии ΔЕµ к изменению температуры ΔТ, вызвавшему это приращение энергии, называют мольной теплоемкостью:
Вставляя в это равенство значение ΔЕµ из (2), получим:
Если идеальный газ нагревается при постоянном давлении, то в этом случае затрачивается дополнительное количество тепла, идущее на совершение работы при расширении газа. Следовательно мольная теплоемкость газа при постоянном давлении Сp будет больше его теплоемкости Сv на величину внешней работы А, т.е. Cp = Cv + A. Величина А = Р ΔV = Р (Vμ' - Vμ), где: Р - давление, Vμ'- мольный обьм газа после нагревания на один градус, Vμ- мольный обьем газа при температуре Т, т.е. при Т+1 = Т'. По уравнению Клапейрона-Менделеева значения РVμ и РVμ' для температур Т и Т' выразится так РVμ = RT и РVμ'=R(T + 1). Вставляя эти значения в выражение работы А, а затем в уравнение теплоемкости Ср получим Ср= Сν + R. (4) Выражение (4) называется уравнением Майера. Отношение теплоемкостей γ=Ср/ Сν в соответствии с равенствами (3) и (4) примет вид
Полученное соотношение теплоемкостей (5) в дальнейшем будет применено для сопоставления с результатами экспериментального измерения.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.012 с.) |

 , (1)
, (1) , (1а)
, (1а) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7) , (8)
, (8) (9)
(9) ,
, , (1)
, (1) i - число степеней свободы.
i - число степеней свободы.

 Частица одноатомного газа рас- z γ β
Частица одноатомного газа рас- z γ β точки. Поступательное движение та- α
точки. Поступательное движение та- α а при ее вращении она не x
а при ее вращении она не x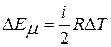 . (2)
. (2)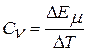 .
. . (3)
. (3) . (5)
. (5)


