Проективная геометрия как путь к целостному пониманию пространства

Георг Глёклер

Эпохи развития геометрии

Математика и геометрия считались в древних культурах подготовкой к посвящению, т.е. к познанию духа.[50]

Математико–геометрическая работа основывается на направленной активности мышления, которое может быть направлено на узнаваемые при помощи органов чувств объекты, или же может не зависеть от них. Так например, числа и линии не были получены путем внешнего чувственного опыта, несмотря на то, что они, конечно же, соотносятся с ним. Собственно математическая деятельность заключается в свободном от чувственного опыта мышлении. Мышление, которое может опираться на само себя, не только не зависит от внешних опор, но кроме этого делает независимым и того, кто мыслит. В этом заключается педагогическое предназначение математики. В соответствии с этим построен учебный план вальдорфской школы. Самой наглядной областью в математике является геометрия. Она непосредственно демонстрирует мыслительные формы, которые имеют большое значение для глубокого понимания пространственно–временных процессов в области эмбриологии, медицины, фармации, ботаники, архитектуры и общей морфологии. Ознакомление с различными предметами на протяжении школьного обучения является грандиозной задачей педагогики, которая стремиться интегрировать духовное измерение в науку.

Геометрия (как и вся математика в целом) относится к важнейшим интегративным наукам, что особенно впечатляюще может реализоваться в вальдорфской педагогике.

Развитие геометрии в контексте эволюции человечества можно разделить на 4 основные эпохи:

1. Геометрия как подготовка к познанию духа, а также как мудрость, инспирирующая архитекторов древних мистерий (Вавилон, Египет, Южная Америка/Тиагуанако/Боливия)

2. Обнародование геометрии Евклидом (365–300 до н.э.), который обобщил дошедшее до него мистериальное знание и сделал его общедоступным в своих элементах (По-видимому, имеется в виду книга Евклида «Элементы геометрии» – прим. перев.). В средневековых монастырских школах труды Евклида наряду с библией были самыми читаемыми книгами. Исходя из этого, математик Георг Унгер высказался, что евклидова геометрия более 2000 лет вплоть до нашего времени способствовала уплотнению сил разума.

3. Эпоха Возрождения, когда художниками была открыта перспектива, благодаря чему стало возможным новое переживание и понимание пространства. Появилось понимание периферии пространства при помощи так называемых удаленных элементов (точка схода, горизонт).

4. На основе того, что было заложено так называемым перспективным рассмотрением, с 17 по 19 век смогла развиться проективная геометрия. В ее основе находится признание того факта, что пространство структурировано двояким образом, т.е. что каждому пространственному образованию соответствует комплементарное образование. Развивая эту идею, Рудольф Штайнер ввел понятие «пространство–противопространство». Проективная геометрия вносит существенное дополнение также и в рассмотрение перспективы. К удаленным элементам точки схода и горизонта, которые использовались в перспективе, добавляется еще и удаленная плоскость. Таким образом, в проективной геометрии три основных геометрических элемента (точка, прямая и плоскость) выступают также и в роли удаленных элементов.

1. Пирамиды как свидетели мистериальной мудрости древних времен[51]

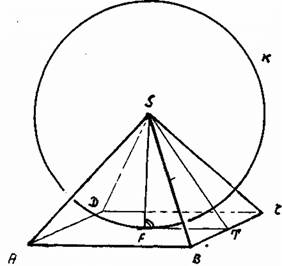
Рисунок 1

Были произведены различные замеры большой пирамиды Хеопса близ Гизы. При этом на примере прямоугольного «вертикального треугольника» SFT обнаружилось, следующее положение вещей (срав. рис.1):

Это число довольно точно соответствует числу g золотого сечения.[52] Это уже примечательно само по себе. Еще более примечательным может быть следующее токование. Вписанный вертикальный круг К с радиусом, равным высоте пирамиды, может рассматриваться как символ круговорота солнца. Если приравнять окружность этого круга к периметру квадрата в основании пирамиды, то получится в точности вышеупомянутое соотношение чисел. Возможно, этот процесс соответствовал так называемой квадратуре круга. Необходимые для этого расчеты приведены ниже:

Расчет:

Разъяснение: если FS = r и ВС = CD =... = s то

(Окружность круга = периметр квадрата в основании)

При этом теорема Пифагора для прямоугольного треугольника SFT)

Далее

После коротких расчетов из этого следует:

Это числовое значение с последовательностью частных наилучших приближений[53] для g с помощью наименьших чисел выражается следующим образом:

Этот результат можно сформулировать следующим образом: если древние египтяне знали число круга, то они могли из него символически выразить число «g», заключив его в «вертикальный треугольник». Если они, напротив, знали число «g» золотого сечения, тогда число круга в свою очередь нашло символическое выражение в окружности «вертикального круга». Для числа круга , исходя из наших предпосылок, после небольших расчетов получилось бы следующее значение: . Вероятно, что при строительстве пирамиды Хеопса использовалось геометрическое знание о том, что число g золотого сечения и число круга необходимо привести в соотношение друг с другом.

2. Пентаграмма, число g золотого сечения и
четыре фундаментальных вывода, связанных с ним

Почему здесь приведен пример из евклидовой геометрии? Она требует нахождения души в конечности пространственных условий на земле. Она описывает их измеримость, обозримость и структурированность. Она опирается на связь чувства жизни с тем, что находится здесь и сейчас, в повседневной жизни, с так называемой предметной реальностью. В рамках этих геометрических эвклидовых законов геометрия пентаграммы занимает особое положение, поскольку в этом случае зримые геометрические законы выходят за рамки чисто геометрического понимания пространства в процессуально–временное измерение. Это происходит благодаря тому, что мыслительные формы, которые развиваются при рассмотрении пентаграммы выходят за понимание пентаграммы как сугубо пространственной фигуры. Мыслительные формы, развивающиеся при рассмотрении пентаграммы ведут к четырем фундаментальным выводам.

Введение

Рисунок 2

Исходя из элементарных знаний геометрии, из рисунка следует, что DG = AG = AB и что оба треугольника АВD и ВGА подобны, т.е. например, что их соответствующие углы равны. Из этого следует:

Отрезок BD делится точкой G таким образом, что малый отрезок BG относится к большому отрезку DG так же, как большой отрезок DG ко всему отрезку BD. Это деление называют золотым сечением (sectio aurea). Оно часто встречается в природе и искусстве, а также и в человеческих формах. Поэтому его называют «божественной пропорцией»[54]. Если принять BD = 1 и DG = g, то исходя из вышеупомянутых расчетов:

, а следовательно: из чего следует .

При этом

Числовая мера g таким образом является квадратным иррациональным числом.

Все квадратные иррациональные числа можно познать конструктивно с помощью циркуля и линейки. Для g получается следующая конструкция:

Рисунок 3

(т–ма Пифагора для прямоугольного треугольника DBF)

из этого следует ;

и в конечном итоге ;

при этом .

С числом g золотого сечения наряду с чисто количественными отношениями связан также и ряд качественных свойств, чей характер выходит далеко за рамки чистой математики. Чтобы должным образом описать эти качества, мы должны прояснить для себя одно очень важное понятие, а именно понятие приближенных значений числа g.

Из g ² + g = 1 сначала следует

Это дает следующее:

Итак, число g может быть представлено в виде т.н. непрерывной дроби.

Для этой непрерывной дроби существуют приближенные значения дробных чисел (так наз. подходящие дроби). Их значения таковы:

 

и т.д.

это уже вполне пригодное приближенное значение для g. Оно составляет

На примере вышеприведенного можно выявить тенденцию, по которой формируются представленные подходящие дроби N₁ N₂, N₃ и т.д. В их числителях и знаменателях находятся числа, относящиеся к знаменитой числовой последовательности, найденной Фибоначчи[55], которая называется последовательностью Фибоначчи:

ее общая формула: f_n = f_n-1 +f_n-2 (для n = 3,4,...)

В последовательности Фибоначчи каждый член равняется сумме двух предыдущих. Из этого следует, что вышеприведенную последовательность приближенных значений для g можно представить в виде последовательности частных двух следующих друг за другом чисел Фибоначчи. Следовательно, числа Фибоначчи в своей основе связаны с числом g.