
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принятие решений голосованиемСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Во многих случаях коллективное решение принимается голосованием. Один из наиболее распространенных принципов голосования – правило большинства: принятой всеми считается альтернатива, получившая наибольшее число голосов. Это правило привлекательно своей простотой, но имеет особенности, требующие осторожного обращения с ним: 1) Оно лишь обобщает индивидуальные предпочтения, и его результаты не являются критерием истины. Только дальнейшая практика показывает, правильным или ошибочным было решение (альтернатива с неопределенными последствиями). 2) Голоса могут разделиться поровну при четном числе голосующих. Это порождает варианты голосования для обеспечения выбора: а) председатель имеет два голоса; б) большинство простое (51%); в) подавляющее большинство (около ¾ голосов); г) абсолютное большинство (близко к 100%); д) принцип единогласия (консенсус, вето). При любом из этих вариантов подразумевается отказ от принятия решения, если ни одна из альтернатив не получила необходимого процента голосов. Так как в реальной жизни отказ от дальнейших действий, следующих за решением, бывает недопустим, а переход к принятию за групповой выбор выбора отдельного лица («диктатора») – нежелательным, разрабатываются различные приемы, сокращающие число ситуаций, приводящих к отказу. Например, два эксперта дали противоположные предпочтения между вариантами а и b. Можно сделать выбор, сравнивая «силу предпочтения» каждого эксперта (если они одинаково компетентны, что в отдельных случаях требует проверки). Можно добавить еще ряд альтернатив: c, d, e. Пусть первый эксперт расположил альтернативы в порядке: c, d, a, b, e. Второй в порядке: b, c, d, e, a. Получается решение в пользу альтернативы b, так как предпочтение второго эксперта сильнее. Казалось бы, исключив возможность отказа от выбора из-за недостижения требуемого большинства, можно обеспечить принятие решения в любых случаях. Но процедура голосования имеет ряд особенностей, известных как парадоксы голосования: 1) Нетранзитивность голосования. Пусть имеется три группы законодателей, голосующих по трем проектам: a, b, c. Альтернативы предъявляются попарно. Каждая группа руководствуется своим набором предпочтений:
Первая: (a > b > c) Вторая: (b > c > a) Третья: (c > a > b). После голосования по паре (a, b) счет будет 2: 1, что a > b; По паре (b, c) 2: 1, что b > c; По паре (c, a) 2: 1, что c > a; То есть a > b > c > a. В случае же применения процедуры, при которой после рассмотрения очередной пары отвергаемая альтернатива заменяется новой, окончательно принятое решение зависит от порядка предъявления альтернатив: при порядке (a, b, c) выбирается c; при порядке (b, c, a) выбирается a; при порядке (a, c, b) выбирается b. То есть результат в руках организатора голосования. Это лишь частный пример более общего явления, получившего название парадокса Эрроу. 2) Возможны любые «перераспределения ресурсов», и все они отражают мнение «всего общества», кроме одного субъекта. Пусть каждый из n субъектов имеет свою долю ai общего ресурса
Пусть а=(а1, а2, …, аn) – состояние сообщества (системы), определяемое распределением ресурса. Другое состояние b=(b1, b2, …, bn) с точки зрения i-го субъекта хуже а, если аi > bi. Будем перераспределять ресурс на основе очень сильного большинства: система перейдет из состояния а в состояние b, если состояние b не хуже состояния а для всех субъектов, кроме одного («тотально-мажоритарное правило»). Последовательность состояний а1, а2, …, аk - тотально-мажоритарный путь из а1 в аk. Пусть а и b – произвольные состояния. При каких условиях существует тотально-мажоритарный путь из а в b? Оказывается, что такой путь существует всегда. Таким образом, опираясь на мнение «всего общества» можно производить любое перераспределение ресурсов, в том числе и представленные на рисунке 1.
S = 16 - ресурс распределен поровну ? ß ß ß
S = 16 ß? ß ß
S = 16 ß ß ?
S = 16 -
Рис.1
3) Вмешательство коалиций в механизм голосования. Вмешательство коалиций в механизм голосования практически меняет его характер. Например, на выборах президента некоторой компании (или государства) борются два партии, стремящиеся сделать победителем своего кандидата. При умении вести дела меньшинство может навязать свое мнение большинству, хотя голосование всегда будет проводиться по правилу большинства. Из рисунка 2 видно, что группа, владеющая восемью голосами, в итоге навязала свое мнение группе из девятнадцати выборщиков. Дело заключается в умелом группировании сил. Но с помощью современных избирательных
Технологий это можно реализовать, и это делается повсеместно с помощью целенаправленного вложения средств, организации агитационных поездок в нужные регионы, разделение территорий на избирательные участки и т.д.
Рис.2
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1846; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.152.153 (0.01 с.) |

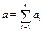 .
.




