Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о коэффициентах роста и градиентах взлетной массы самолетаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В процессе проектирования самолета постоянно приходится сталкиваться с решением задач на противоречия массы и аэродинамического сопротивления, массы и ресурса, массы и стоимости конструкции и т.д. Изложению методики решения подобных задач и посвящен разд. 3.2. На всех стадиях проектирования самолета обычно вносятся различные изменения и улучшения, сравниваются варианты конструкторских решений. Вопрос состоит в том, как достаточно корректно произвести эти операции, как связать частные изменения различных величин с общим изменением критерия оценки самолета? Решение может дать приближенный метод, основанный на линеаризации малых (конечных) приращений. Наиболее просто задача решается в тех случаях, когда за критерий оценки принимается величина взлетной массы самолета. Метод основан на следующих допущениях: – частные (локальные) изменения, если они вносятся одновременно, непосредственно не связаны между собой, являются независимыми и определяются конструктором; – внося какие-либо изменения в проект, конструктор стремится сохранить заданную целевую нагрузку и основные летные данные согласно ТЗ или ТТТ; – изменения малы, не превышают 10... 15 % исходного значения (чем больше величина изменения, тем больше погрешность метода – см. ниже). На основании первого из этих допущений полный дифференциал критерия оценки (а) имеет вид:
где i – параметр. Считая, что дифференциалы и конечные приращения эквивалентны, уравнение (3.25) можно записать так:
Возьмем в качестве критерия взлетную массу самолета (m0), а в качестве изменяемых независимых параметров – дополнительную массу какой-либо части самолета (Dmдоп), приращение силы лобового сопротивления (ΔΧ0), приращение еще некоторого параметра (Δin), влияющего на m0. Тогда уравнение (3.26) примет вид:
Здесь слагаемые правой части и есть градиенты взлетной массы самолета:
В данном случае grad m0 являются однонаправленными векторами. Производные Простота и удобство метода градиентов взлетной массы состоит в том, что на всех стадиях проектирования самолета коэффициенты роста являются константами и могут быть заранее вычислены, а конечные приращения (Dm0доп, ΔΧ0 и т.д.) целиком определяются конструктором.
Рис. 3.2. Зависимость взлетной массы самолета от дополнительной массы: 1 – точное решение по уравнению весового баланса самолета; 2 – решение методом градиентов взлетной массы самолета. Метод градиентов позволяет решать весьма большой круг задач: 1) определять влияние на критерий оценки самолета каждого из переменных параметров, выявить, какой из них оказывает наибольшее влияние, чтобы направить усилия в первую очередь на улучшение этой величины. Для решения данной задачи необходимо найти соответствующие частные производные и принять, что конечные приращения переменных должны составлять одинаковую, сравнительно небольшую часть первоначального значения каждой из них (например, 1 %); 2) определять суммарное, зачастую противоречивое, влияние на критерий оценки какого-либо числа величин. Практический интерес эта задача имеет при анализе различных вариантов технических решений, связанных, например, с изменением массы, силы лобового сопротивления, ресурса и стоимости. Очевидно, что наилучшим будет тот вариант решения, для которого имеет место экстремум критерия, например, экстремум приведенных затрат, т.е. [Σ(–Dа)]mах или [Σ(+Da)]min; 3) находить эквиваленты различных пар величин, например весовые эквиваленты стоимости или ресурса агрегата и т.д. Эта задача имеет весьма большое практическое значение при исследовании целесообразности проектно-конструкторских решений, связанных, например, с применением более легкой, но более дорогой конструкции, с уменьшением аэродинамического сопротивления за счет увеличения массы и т.п. Для решения таких задач необходимо приравнять нулю пару каких-либо частных приращений критерия (данная задача рассмотрена ниже). Заметим, что в общем случае пользуются формулой
Решение этой задачи рассмотрено в разд. 3.2.4; 4) пересчитывать значение взлетной массы на новое значение, пользуясь простой формулой
Степень погрешности при определении значения (т0)нов зависит от абсолютной величины приращения параметра Δi (рис. 3.2). Если величина Δi не превышает 10 % от первоначального значения параметра, что часто имеет место при рассмотрении различных модификаций характеристик и параметров самолета, то с помощью линеаризации уравнения т0 (Δi) по формуле (3.29) значение (m0)нов можно определить с точностью до 1 %. Такая точность при приближенных расчетах обычно вполне удовлетворяет конструктора. Таким образом, метод градиентов взлетной массы позволяет при меньших затратах труда по сравнению с обычным расчетом новых вариантов самолета найти в процессе проектирования связи между частными и общими изменениями характеристик, сравнить между собой частные изменения характеристик при одинаковом конечном результате, дать оценку целесообразности проектно-конструкторских решений. Указанные задачи могут решаться на любом этапе проектирования опытного образца или при модификациях уже построенного и эксплуатируемого самолета. При этом ограничения (условия решения) задач на каждой стадии могут быть различными. Например, на стадии предварительных изысканий и эскизного проектирования опытного самолета основными ограничениями являются как заданные параметры (Lpaсч, mц.н) = const, так и обычно принимаемые (р0, `Р0) = const. На более поздней стадии проектирования или при модификации существующего образца самолета, когда определены характеристики двигателей, размеры и форма самолета, ограничением может служить (S, Р0) = const. Кроме того, на каждой стадии проектирования известно, какие летные данные должны быть сохранены при изменении других характеристик самолета. Например, при появлении дополнительной массы агрегата или детали, когда требуется сохранить не только прочность конструкции и расчетную дальность полета, но также и крейсерскую скорость, увеличение взлетной массы будет различным при (p0, P0) = const и при (S, Р0) = const. Остановимся на определении некоторых наиболее важных производных взлетной массы в простейших случаях, когда изменяется только какая-либо одна частная характеристика агрегата (например, масса), а остальные частные характеристики (аэродинамические, объем и т.п.) остаются неизменными. 3.2.2. Производная взлетной массы (коэффициент роста) по дополнительной массе частей самолета. В процессе проектирования самолета нередко встречается следующая задача: решено изменить массу какого-либо агрегата, группы оборудования или нагрузки, сохранив аэродинамические и другие характеристики самолета. Насколько при этом надо изменить взлетную массу, чтобы основные летные характеристики и прочность самолета остались прежними? Такие задачи характерны для стадии эскизного проектирования, когда на основе вариаций различных параметров выбираются основные размеры и рассчитывается масса самолета. Однако и на последующих стадиях разработки проекта (даже при модификациях построенного самолета) эти задачи не исключаются, так как детальная проработка конструкции самолета обычно сопровождается некоторыми отклонениями массы агрегатов от их значений, установленных при эскизном проектировании. Итак, допустим, что на какой-либо стадии проектирования самолета появилась необходимость ввести дополнительную массу mдоп. Если при изменении массы какого-либо агрегата на (mдоп)1 нужна еще дополнительная масса (mдоп)2 для исправления возможного изменения центровки самолета, увеличения жесткости конструкции и т.п., то будем считать, что дополнительная масса mдоп является суммой всех этих составляющих, т.е. mдоп = (mдоп)1 + (mдоп)2 +... Пусть известны зависимости массы всех составляющих от взлетной массы самолета, а также величины, которые конструктор считает нужным оставить неизменными, например (р0, `Р0) = const или (S, P0) = const, или `mт = const и пр. Требуется определить увеличение взлетной массы, необходимое для выполнения поставленных ограничений (от которых зависит сохранение летных характеристик), а также для сохранения прочности конструкции. Запишем уравнение весового баланса самолета при появлении дополнительной массы: m0 = mпуст + mт + mц.н + mcл + mдоп, (3.30) где mпуст – масса пустого самолета, mпуст = f1(m0); mт – масса топлива, mт = f2(m0); mц.н, mcл – целевая и служебная нагрузки, (mц.н, mcл) = const. Из (3.30) следует, что mдоп = m0 – mпуст – mт – mц.н – mcл Возьмем частную производную по m0:
Так как требуется определить производную д m0/ д mдоп, то на основании предыдущего имеем
Найденная производная и есть коэффициент роста взлетной массы в связи с появлением дополнительной массы. Обозначим для краткости
Численные значения cm могут изменяться от единицы до бесконечности. Последнее возможно, когда д / д m0(mпуст + mт) = 1. Если же д / д m0(mпуст + mт) = 0, то cm = 1. При этом (mпуст, mт) = const и (m0)нов = (m0)исх ± mдоп, что соответствует случаю, когда изменяются все летные характеристики самолета и прочность его агрегатов (этот случай возможен при модификации построенных самолетов). Важно отметить, что величина cm может быть больше единицы лишь в том случае, когда с введением дополнительной массы конструктор стремится сохранить неизменными какие-либо свойства самолета – летные данные, прочность и т.п. Рассмотрим физическую сущность возникновения производной cm, когда cm > 1. Допустим, что на проектируемом самолете потребовалось установить дополнительное оборудование массой mдоп, которое не ухудшает аэродинамику и не требует увеличения объема самолета. Необходимо, сохранив основные летные характеристики, полезную нагрузку, а также прочность агрегатов, модифицировать самолет. Для сохранения летных характеристик, очевидно, нужно сохранить нагрузку на 1 м2 крыла р0 и тяговооруженность `Р0 при взлете. С увеличением массы самолета на mдоп возрастает и нагрузка на крыло, фюзеляж, шасси и оперение. Следовательно, для сохранения прочности этих агрегатов требуется увеличить размеры и массу их силовых элементов. Однако для выполнения условия p0 = m0/S = const необходимо с изменением m0 соответственно изменить размеры крыла, а при `Р0 = const – тягу двигателей, что само по себе повлечет за собой изменение массы крыла и силовой установки. Далее, с увеличением размеров крыла приходится увеличить также размеры и массу оперения для сохранения неизменными характеристик устойчивости самолета. Наконец, для сохранения дальности полета потребуется, очевидно, увеличить и первоначальный запас топлива, учитывая условие mт = const. Приведенное увеличение массы отдельных частей самолета и исходного запаса топлива приведет к увеличению взлетной массы самолета, которое, в свою очередь, повлечет за собой повышение нагрузки на агрегаты и увеличение их массы. В результате потребуется новое, вторичное увеличение массы агрегатов и топлива. Процесс заканчивается тогда, когда взлетная масса достигает значения, полученного из решения уравнения весового баланса. Таким образом, приращение массы самолета mдоп повышает взлетную массу на значительно большую величину cmmдоп. Производная д m0/ д mпуст, входящая в (3.31), определяется по формуле:
Здесь mкр, mф, mоп, mш, mс.у, mоб.упр – масса крыла, фюзеляжа, оперения, шасси, силовой установки, оборудования и управления. Весовые формулы крыла и других агрегатов в зависимости от m0 обычно известны (см. гл. 6). При определении производной д mт/ д m0, также входящей в (3.31), следует учитывать, что масса топлива линейно связана с взлетной массой, и поэтому д mт/ д m0 = `mт. Для приближенных расчетов можно использовать следующую зависимость, вытекающую из формулы Бреге:
Если mт £ 0,2, то формулу (3.32) можно упростить. Раскладывая второе слагаемое в ряд и ограничиваясь двумя первыми членами разложения, получим с погрешностью ±2 %
где 1,1 – поправочный коэффициент; L – расчетная дальность полета, км; Cр, К – средние за полет значения удельного часового расхода и аэродинамического качества; Vрейс – рейсовая скорость, км/ч. Приближенно можно считать, что д mпуст/ д m0» `mпуст. Тогда формула (3.31), учитывая (3.32), примет простой расчетный вид:
Эта формула может применяться на ранних стадиях проектирования самолета. Коэффициент роста cm можно определить также, исходя из принципа линейного подобия:
где kп = 2,2...2,6 – коэффициент линейного подобия. Формула (3.35), как и (3.34), может применяться на ранних стадиях проектирования. В табл. 3.2 приведены значения коэффициента роста взлетной массы cm для пассажирских реактивных самолетов. При (S, Р0) = const величина cm значительно меньше, чем при (р0, `Р0) = const. Это объясняется тем, что дополнительная масса при (р0, `Р0) = const влечет за собой увеличение массы всех входящих в m0 составляющих, кроме коммерческой mком и служебной mсл нагрузок, так как обычно (mком, mсл) = const. При (S, P0) = const масса силовой установки и часть массы крыла, зависящая от его площади, остаются неизменными. Приведенная методика расчета cm не учитывает происхождения дополнительной массы mдоп. В каком бы агрегате самолета (крыло, фюзеляж и т.д.) не образовалась дополнительная масса, изменение взлетной массы будет одинаковым и равным cmmдоп. При более точном расчете cm можно учесть и место образования дополнительной массы. Расчеты показывают, что чем дальше от центра масс самолета возникает дополнительная масса, тем больше значение cm. По сравнению с приведенными формулами значение cm может увеличиться на 15... 20 %, если дополнительная масса появилась на конце крыла или фюзеляжа. Таблица 3.2 Значения коэффициента роста взлетной массы пассажирских самолетов
Производная cm не только упрощает определение новой взлетной массы на любой стадии проектирования, но и позволяет судить о весовом совершенстве проектируемого самолета. Очевидно, что чем больше величина cm, тем больше требуется затрат времени и средств на уменьшение массы каждого агрегата, узла и детали. 3.2.3. Производные взлетной массы (коэффициенты роста) по аэродинамическим характеристикам самолета Рассмотрим, как влияют аэродинамическое качество K, сила лобового сопротивления Х0 (при Cу = 0) и коэффициент Cх0 на взлетную массу самолета. Основные исходные условия, как и прежде: (Lpaсч, mд.в) = const, а также (р0, 0) = const или (S, 0) = const. Нетрудно показать, что при вариациях Х0, К и Сх0 крейсерская скорость за счет изменения высоты полета может остаться неизменной, т.е. Vкрейс = const, что означает Vрейс = const, так как Lpaсч = const. Задача состоит в том, чтобы подобно найденной в разд. 3.2.2 производной д m0/ д mдоп определить д m0/ д К, д m0/ д Х0, д m0/ д Сх0. Для этого воспользуемся уравнением весового баланса самолета в относительных величинах (все составляющие массы отнесены к величине взлетной массы): 1 = mпуст + mт + mц.н + mсл, где mт – как в формуле (3.32). Следовательно, 1 = пуст + ц.н+ сл + 1 – откуда среднее потребное значение аэродинамического качества равно
Аэродинамическое качество здесь является не только явной функцией величин, стоящих в правой части равенства (3.36), но зависит также и от размеров самолета. Масштабный эффект проявляется, если изменение m0 связано с изменением размеров самолета. Масштабный эффект является следствием зависимости аэродинамического качества от числа Рейнольдса, куда входит характерный размер самолета (хорда крыла). Для дозвуковых самолетов К = Кср» 12,5 + 0,0331 Подъем и снижение дозвуковых самолетов ведутся, как правило, при аэродинамическом качестве, которое мало отличается от крейсерского. Поэтому для дозвуковых самолетов с достаточной точностью можно принимать К = Ккрейс. Возьмем частную производную К по m0 и запишем ее в виде обратной, интересующей нас, величины д m0/ д К. В результате получим, считая mн.з = const,
В случае, когда размеры самолета не изменяются при изменении аэродинамического качества, т.е. при условии (S, Р0) = const производная (д К/ д m0)* = 0 и
Если относительная масса топлива т ≤ 0,2, то, учитывая (3.33), получим более простую формулу
Найдем теперь, как изменяется взлетная масса при изменении силы лобового сопротивления самолета Х0 (при Су = 0). В этом случае (Здесь имеется в виду средняя за время полета сила Х0 = Сx0Sq = (X0)cp, так как (Сх0, q)» const в течение всего полета.), как нетрудно показать, можно сохранить скорость полета, если (Сх, Су, ρ, λ) = const при Μ < 1 или (Сх, Су, ρ, Частная производная д m0/ д Х0 выражается через cκ:
При дозвуковой скорости
где m, К – средние за время полета масса самолета и аэродинамическое качество, m» m0 – 0,5mт.расх; (λэф, Сх) = const. При этих условиях и числе Μ < 1
а при числе Μ > 1
Подставляя в (3.40) д Х0/ д К из (3.41), получим при числе Μ < 1
при числе Μ > 1
Иногда более удобно определять изменение взлетной массы не в зависимости от изменения силы лобового сопротивления Х0, а в зависимости от изменения ее коэффициента Сх0. В этом случае, принимая, как и ранее, при числе Μ < 1 (Сх, Су, ρ, λ) = const, а при числе Μ > 1 (Сх, Су, ρ,
При Μ < 1 из уравнения поляры имеем
откуда Су = Следовательно, при Μ < 1
По аналогии при Μ > 1
Учитывая, что при числе Μ < 1
(здесь Кmах – исходное значение качества до изменения Cх0, при котором Cх – Сx0 = Сxi = Сx0), из (3.46) имеем
Соответственно и при Μ > 1 получаем
Подставив в (3.45) д К/ д Сх0 из (3.48) и обозначив = χСх0, получим при числе Μ < 1
при числе Μ > 1
В табл. 3.3 приведены примерные расчетные значения производных χК, χХ0и χСх0 для пассажирских самолетов. Таблица 3.3 Значения коэффициентов роста взлетной массы χК (кг/единица качества), χХ0 (кг/даН) и χСх0
Из сравнения значений χm и χХ0, (см. табл. 3.2 и 3.3) видно, что увеличение Х0 на 1 даН влечет за собой при прочих равных условиях значительно большее увеличение взлетной массы, чем пере-тяжеление на 1 кг какого-либо агрегата. Этот вывод особенно нагляден для тяжелых самолетов. Следует заметить, что возможен случай, когда изменение массы агрегата или узла связано с изменением его объема, причем известна зависимость силы вредного аэродинамического сопротивления Х0 от объема U. Тогда формула для определения χm с учетом изменения объема агрегата примет вид:
Аналогично могут быть получены формулы для χm в случаях, когда изменение массы и объема агрегата связано с изменением каких-либо других аэродинамических характеристик (аэродинамического качества и т.д.). Аналогично рассмотренным в разд. 3.2.2. и 3.2.3 коэффициентам роста взлетной массы можно получить расчетные формулы и для других коэффициентов роста m0, например в связи с изменением удельного часового расхода топлива, тяговооруженности и других интересующих конструктора величин.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |



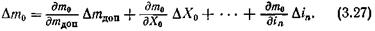
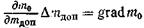 – в связи с появлением дополнительной массы;
– в связи с появлением дополнительной массы; – в связи с появлением дополнительного лобового сопротивления, и т.д.
– в связи с появлением дополнительного лобового сопротивления, и т.д. принято называть коэффициентами роста взлетной массы.
принято называть коэффициентами роста взлетной массы.
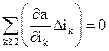 (3.28)
(3.28)
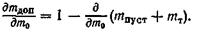

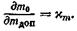





 + н.з,
+ н.з,
 и, следовательно, (д К/ д m0)* = 0,0114/
и, следовательно, (д К/ д m0)* = 0,0114/  , где m0 в кг; для сверхзвуковых (д К/ д m0)* = 0,173/
, где m0 в кг; для сверхзвуковых (д К/ д m0)* = 0,173/  , где m0 в т.
, где m0 в т.


 ) = const при Μ > 1.
) = const при Μ > 1.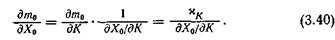







 .
.