
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Електричні процеси в коаксіальних лініях передачіСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Здатність коаксіальної пари пропускать широкий спектр частот сигналів забезпечується конструктивно шляхом коаксіального (одноосного) розташування внутрішнього і зовнішнього провідників. Особливості розповсюдження електромагнітної енергії по коаксіальній парі обумовлює можливість передачі широкого спектру частот сигналів і має переваги в порівнянні з низькочастотними (симетричними) лініями передачі. В коаксіальній конструкції кабелів зв”язку взаємодія електромагнітних полів внутрішнього (центральна жила) і зовнішнього (у вигляді циліндра) провідників коаксіальної пари таке, що зовнішнє поле дорівнює нулю (див. Рис. 16). Рис. 16. Конфігурація магнітного поля в коаксіальній парі
В металічному провіднику а магнітне поле наростає до поверхні, а потім зменшується зі збільшенням координати r відповідно до закону Ампера:
де r – радіальна координата, а І – величина струму, який протікає в провіднику. В металічному провіднику б магнітне поле наростає також до зовнішньої поверхні циліндра і спадає за межами його по такому ж закону. Оскільки ці струми направлені в різні сторони, то результуюче магнітне поле буде різницею цих магнітних полів і буде зосереджене тільки всередині цього коаксіала:
Силові лінії магнітного поля зосереджені всередині всередині коаксіальної пари у вигляді концентричних кіл, а зовні коаксіала магнітне поле відсутнє. Електричне поле всередині коаксіальної пари також замикається між провідниками а і б по радіальним напрямкам і за її межами дорівнює нулю. Якщо коаксіальну пару розташувати так, щоб її вісь співпадала з віссю z, то електромагнітне поле внаслідок циліндричної симетрії не буде залежати від координати φ. Крім того, компонента магнітного поля вздовж z - осі буде відсутня по визначенню поперечності електромагнітного поля. Також буде відсутня тангенціальна компонента напруженості електричного поля Е φ і радіальна компонента напруженості магнітного поля Н r. Отже, в коаксіальній парі ідеальної конструкції діють лише три складові (компоненти) електромагнітного поля: Е r, Е z, Н φ (див. Рис. 16): Електричні процеси в коаксіальній лінії передачі для цих компонент електромагнітного поля можна описати за допомогою рівнянь Максвелла в такому вигляді:
Рис. 17. Конфігурація компонент електричного і магнітного поля в коаксіальній парі. Напруженість магнітного поля коаксіальної пари має тільки одну складову Н φ. Це означає, що лінії магнітної індукції розташовуються концентричними колами навколо z –осі. Електричне поле характеризується двома складовими: радіальною Е r і повздовжньою Еz. Повздовжня складова Е z характеризує струм провідності в провідниках, який направлений вздовж кабелю в протилежні сторони. Для вивчення електричних явищ, які проходять в коаксіальній парі, необхідно розглянути два процеси: розповсюдження енергії вздовж пари і поглинання її провідниками (внутрішнім і зовнішнім). У першому випадку енергія направлена вздовж осі z, а в другому – всередину провідників по координаті r. Обидва процеси оцінюються і характеризуються за допомогою теореми Умова – Пойтінга. Передача енергії по коаксіальній лінії. Потік енергії вздовж коаксіальної лінії визначається законом Умова - Пойтінга, за яким: вектор розповсюдження енергії вздовж лінії утворює з компонентами електричного Е і магнітного Н полів правогвинтову систему:
Для встановлення розподілу напруги і струму вздовж провідників необхідно знайти величини Е r і Н φ як функції змінної z. Причому для цих складових поля вздовж осі z діє експоненціальний закон затухання у вигляді:
Де γ – коефіцієнт поширення хвилі, а Е rо і Н φо – початкові амплітуди цих векторів електричного і магнітного полів. Енергія на шляху поширення хвилі зустрічає опір середовища Z z, яке математично записується як відношення цих компонент, які зв’язані між собою рівняннями Максвелла в циліндричних координатах:
Продиференціювавши ці компоненти по z і підставивши їх в рівняння Максвелла маємо:
З цих останніх двох рівнянь отримаємо вираз для коефіцієнту розповсюдження сигналу вздовж z –осі:
де μа, εа, σ - відповідно магнітна, діелектрична проникність і провідність середовища коаксіального кабелю. Для хвильового опору коаксіальної пари провідників необхідно оперувати величинами напруги між провідниками і струму, що протікає по провідниках: Zв = U / I. Виразимо напругу між провідниками через радіальну компоненту електричного поля E r:
Для радіальної компоненти Е r отримаємо вираз:
Зробивши ряд перетворень, отримаємо вираз для хвильового опору через радіуси коаксіального кабелю r a і r b, μа, εа, σ і ω:
Первинні параметри R, L, C, G ми визначимо використавши співідношення:
В реальних умовах провідники мають кінцеву провідність σ і створюють реальні втрати енегії на джоулеве тепло. Вони вираховуються із загального виразу:
Повний опір коаксіального кабелю визначається як сума двох хвильових опорів провідників а і б:
В цьому виразі R а – активний опір центрального провідника; L а – внутрішня індуктивність провідника; σ - провідність центрального провідника а, r a – його радіус, а k – хвильовий вектор. Повний опір коаксіальної лінії визначиться, якщо в рівняння для опору підставимо значення Е r і Н φ для одного з провідників а. Аналогічно поступаємо при розрахунку індуктивности L. В результаті отримаємо формули для розрахунку Ra, La:
В області високих частот внутрішня індуктивність мала і результуюча індуктивність коаксіальної кабельної лінії обумовлена тільки індуктивністю зовнішнього провідника L вш:
Для коаксіального кабелю з мідними провідниками формули для розрахунку мають вигляд:
Ємність і провідність ізоляції коаксіальних ліній. Під дією змінного електромагнітного поля в діелектриках-ізоляторах, які не мають вільних електронів і складаються з іонів і діполів (іон-зв”язаний електрон на ньому) відбувається зміщення діполів, їх переорієнтація і поляризація. Поляризація – це зміщення додатніх і відємних зарядів в діелектрику під впливом зовнішнього електричного поля. Змінна поляризація викликає появу і дію струмів зміщення – ємністних струмів Ізм, що приводить до затрат енергії на переорієнтацію діполів. Чим вища частота електромагнітних коливань, тим більші за величиною струми зміщення – тим більші втрати енергії. При постійному струмі ці явища відсутні. Описані вище явища в діелектриках характеризуються двома параметрами: ємністю С (вона визначає здатність до поляризації діелектрика і величину струмів зміщення) і провідністю G, яка характеризується втратами енергії в діелектриках. Ємність коаксіального кабелю аналогічна ємності циліндричного конденсатора, в якому провідниками є центральна жила і зовнішній екран, а діелектриком служить розташований між ними ізолятор або повітря. Внаслідок осьової симетрії напруженість електричного поля Е має однакові потенціали на певних віддалях від центру кабеля. Провідність ізоляції і ємність коаксіального кабелю в залежності від його розмірів діаметрів поперечного перерізу ra і rb розраховується по формулах: Провідність ізоляції G прийнято виражати через тангенс кута діелектричних втрат в ізоляції кабелю. Тоді формули матимуть вигляд:
В загальному вигляді, крім провідності ізоляції, яка обумовлена діелектричними втратами G, необхідно враховувати провідність, яка визвана струмом витоку через недосконалість ізоляції: Giz = 1/ R iz. По величині ця провідність ізоляції обернено пропорційна опору ізоляції кабеля, яка для коаксіального кабелю повинна бути не менша за 10000 МОм на 1 км. Таким чином, провідність ізоляції коаксіального кабелю вираховується за формулою: G = По абсолютній величині для певного діапазону частот другий доданок значно більший по величині ніж перший.
Аналіз частотної залежності первинних параметрів коаксіального кабелю R, С, L і G показує, що активний опір R закономірно зростає за рахунок поверхневих струмів і ефекту близкості при зростанні частоти, причому опір внутрішнього провідника Rа>>R б в 3-4 рази. Індуктивність L зі збільшенням частоти зменшується. Це визвано тим, що внутрішня індуктивність зменшується за рахунок поверхневих ефектів, а зовнішня індуктивність не змінюється із збільшенням частоти. Ємність С не залежить від частоти тому, що визначається геометричними розмірами кабелю і діелектричною проникністю ізолятора. Провідність G ізоляції коаксіального кабелю з ростом частоти лінійно зростає. Величина її залежить в першу чергу від діелектричних втрат в кабелі – тангенса кута діелектричних втрат tg δ. Залежність первинних параметрів коаксіального кабелю від геометричних (відношення зовнішнього діаметра до діаметра центральної жили) розмірів показує, що індуктивність L зростає, а ємність С і провідність ізоляції G зменшується. Активний опір R залежить не від відношення радіусів, а від абсолютних значень товщини проводящих жил: чим товщий провідник, тим менший активний опір.
Рис. 18. Залежність від частоти первинних параметрів для коаксіального кола. Вторинні параметри (хвильовий опір Z хв, коефіцієнт затухання α, коефіцієнт фази β і швидкість розповсюдження хвилі υ) коаксіальних кабелів, які використовуються в частотному діапазоні від 60 кГц і вище, розраховуються за формулами:
Вирази для вторинних параметрів коаксіального кабелю через його габаритні розміри (d і D) та параметри ізоляції (ε і tg δ) мають вигляд:
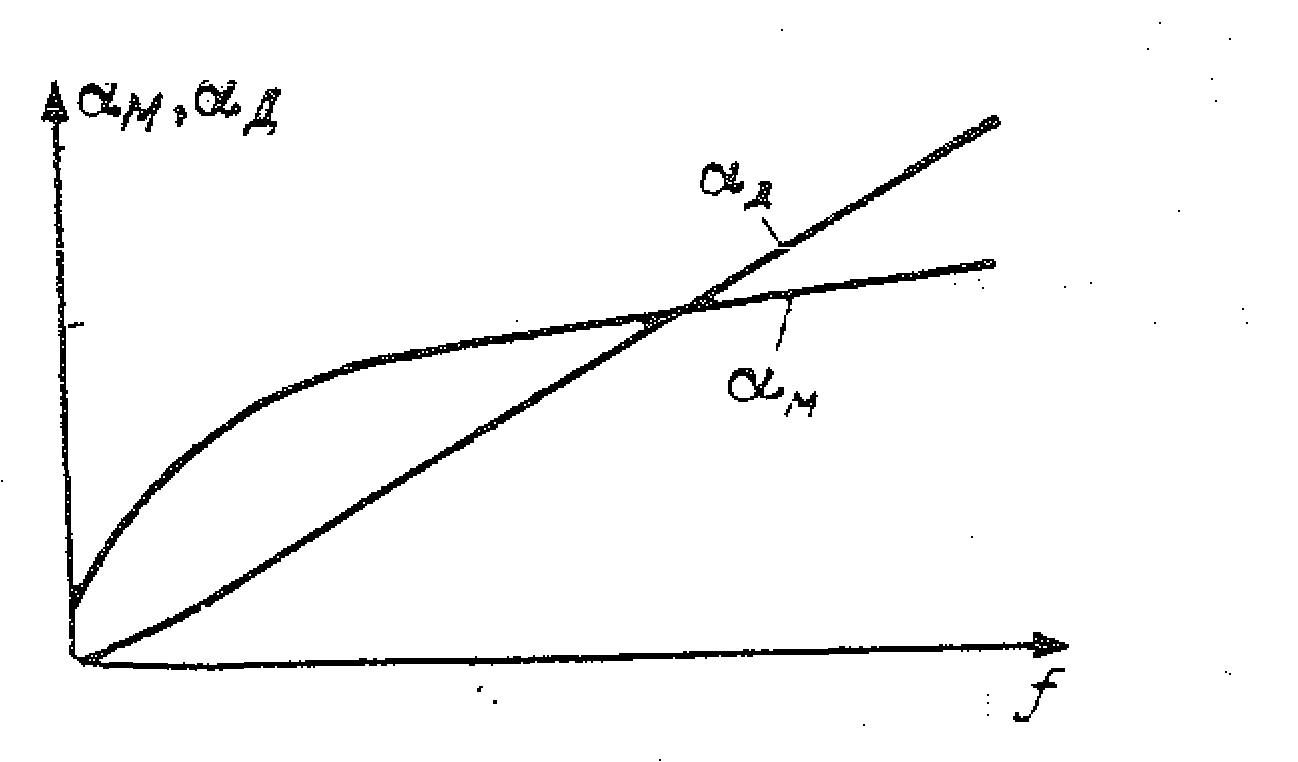
де α М - коефіцієнт затухання в металі, а α Д - коефіцієнт затухання в діелектрику. Рис. 19. Частотна залежність коефіцієнта затухання для коаксіального кабелю:
При малих частотах затухання в металічних провідниках більше, ніж в діелектрику, а при високих – навпаки. Тоді:
З наведеної формули видно, що коефіцієнт фази зростає зі збільшенням частоти лінійно. Це обумовлює майже постійну швидкість передачі енергії по коаксіальному кабелю у всьому спектральному діапазоні частот і зменшується при зростанні діелектричної проникності ізолятора. Швидкість передачі енергії по коаксіальній мережі вища, ніж по симетричній парі і наближається до швидкості розповсюдження електромагнітних хвиль в повітрі (c = 300000 км/с).
В коаксіальному кабелі з суцільним діелектриком (ε = 2,3) Zo = 50 Ом, а при комбінованій ізоляції (ε = 1,1) величина хвильового опору складає приблизно 75 Ом. Хвильовий опір Z хв коаксіальної пари для високих частот визначається формулою:
Або:
|
||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.0.57 (0.013 с.) |







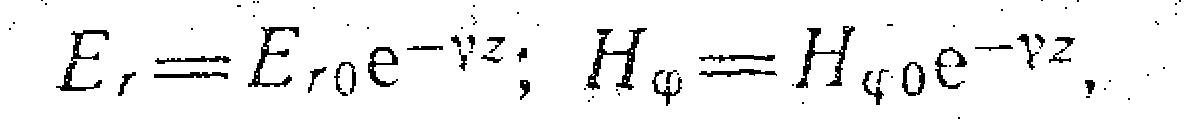











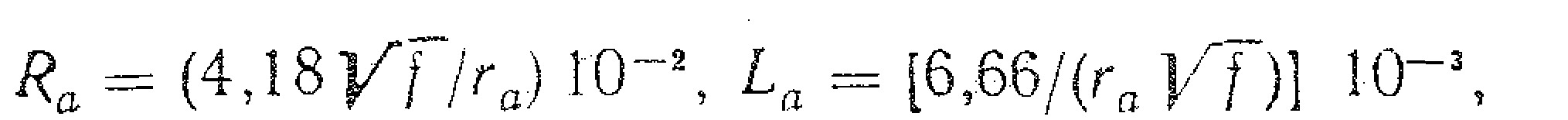

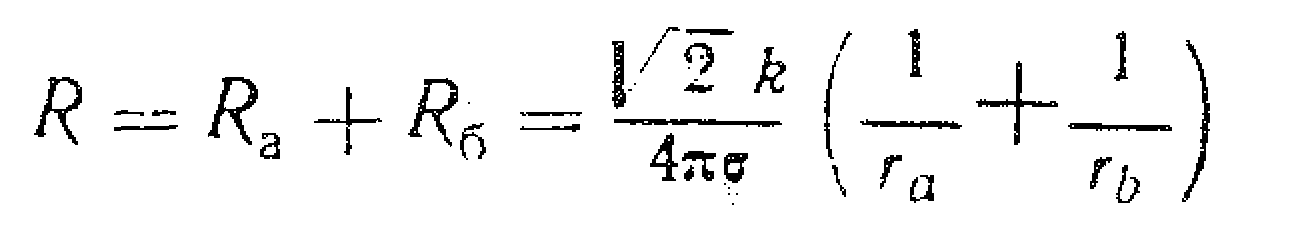
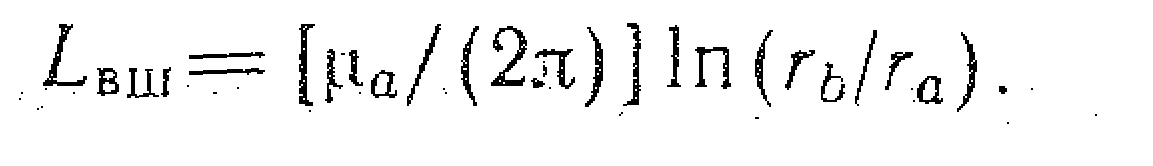






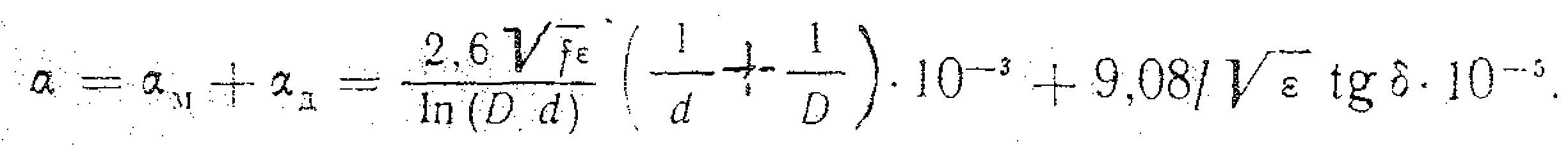
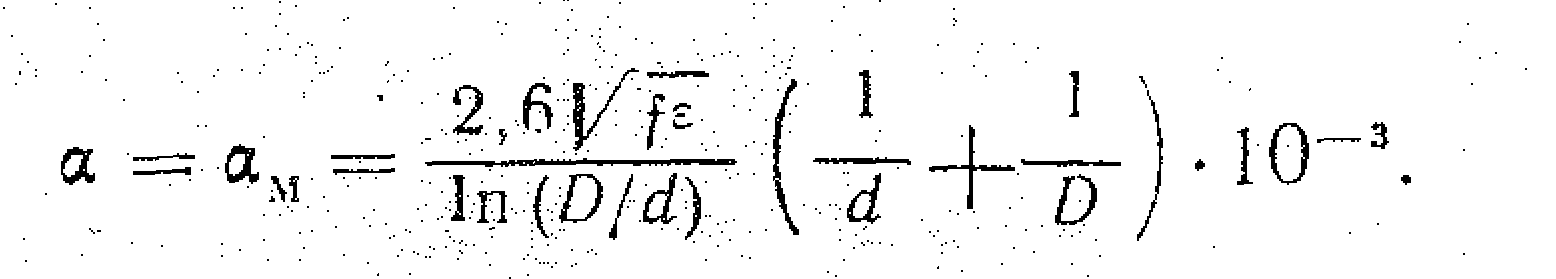 Коефіцієнт зсуву фаз β визначає довжину хвилі, розповсюджувану в кабелі:
Коефіцієнт зсуву фаз β визначає довжину хвилі, розповсюджувану в кабелі:








