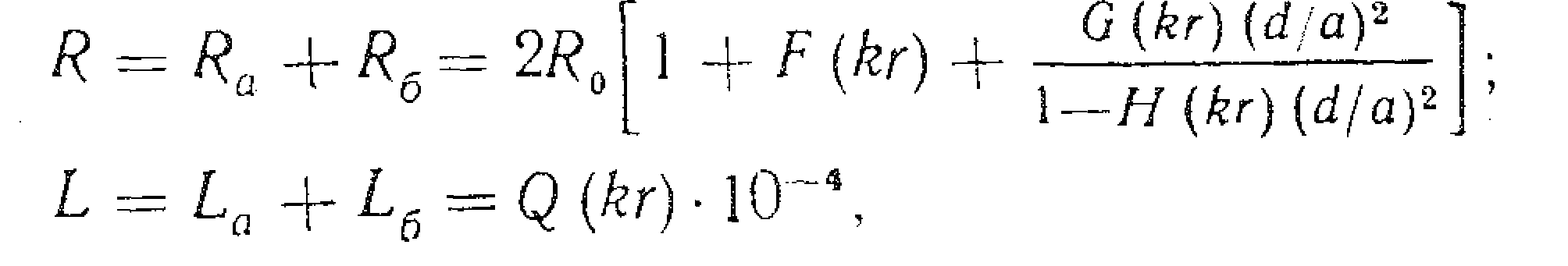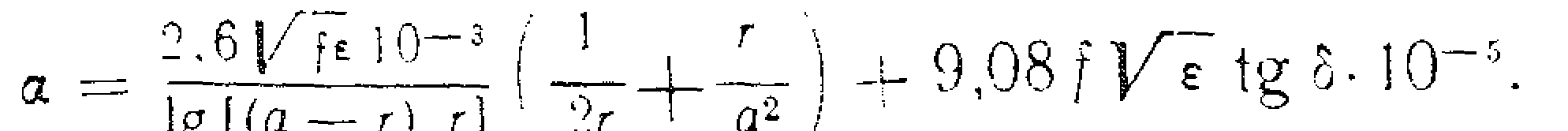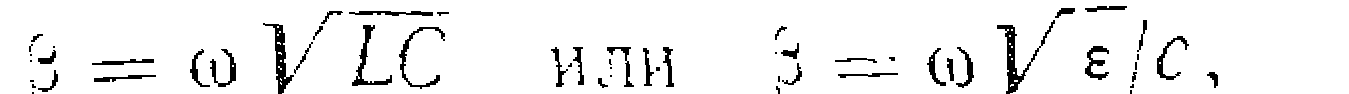Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Електричні процеси в симетричних лініяхСодержание книги
Поиск на нашем сайте
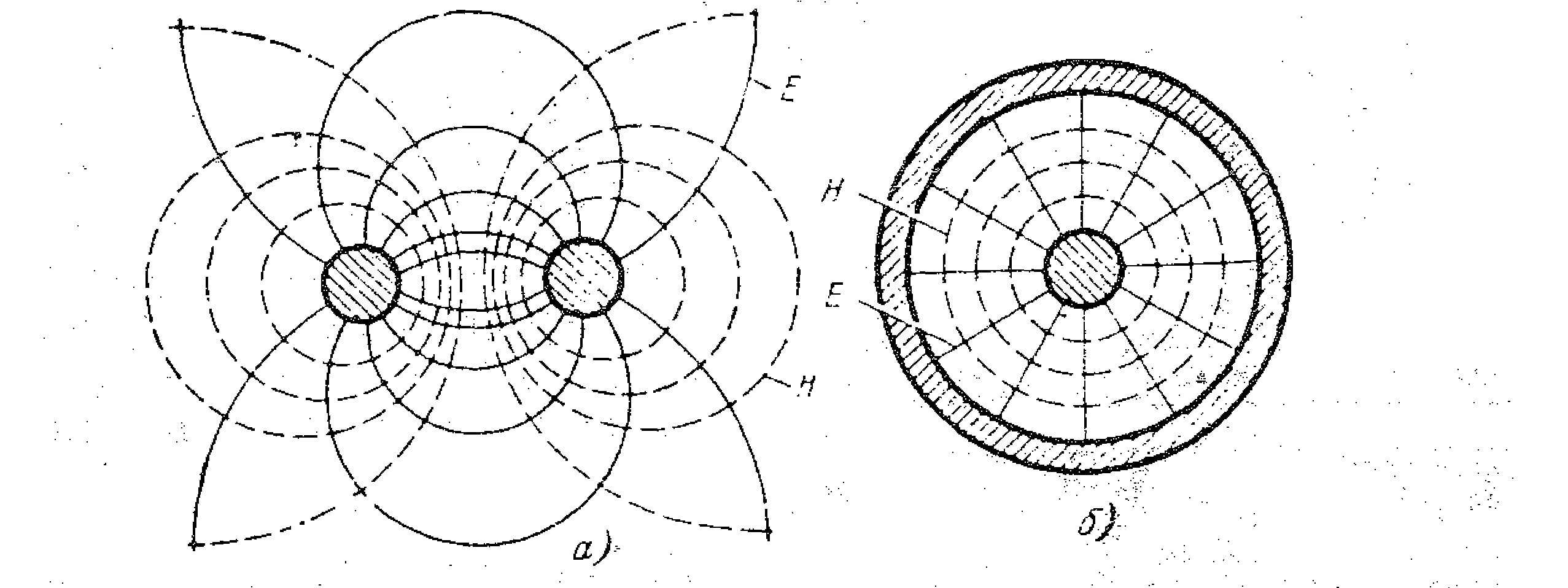
На відміну від коаксіальних кабелів в симетричному кабелі електромагнітне поле випромінюється в навколишнє середовище на значні відстані від проводової лінії. Під дією змінного поля відбувається перерозподіл електромагнітної енергії по перерізу провідників і спостерігаються такі явища: поверхневий ефект, ефект близькості сусідніх провідників, вплив на параметри лінії оточуючих металічних мас (сусідніх провідників, екрану, броні). Причому, в симетричних кабельних ланцюгах мають місце всі три фактори одночасно. В повітряних лініях, в яких провода розташовані порівняно далеко один від одного і відсутні зовнішні металеві оболонки, необхідно враховувати лише поверхневі ефекти. Рис. 14. Розподіл напруженості електричної Е і магнітної Н компонент електромагнітного поля для симетричного (а) і коаксіального (б) кабелів.
За рахунок перерахованих явищ відбувається перерозподіл електромагнітного поля і змінюються параметри ланцюгів: зростають по величині активний опір R і ємність C, а індуктивність L зменшується. Найбільш суттєво зростає опір лінії: R = R0 + Rпе + Rеб + R зм, де R0 - опір постійному струму; R пе - опір за рахунок поверхневого ефекту; Rеб - опір за рахунок ефекту близькості; R зм опір визваний втратами в присутніх навколишніх металічних обєктах за рахунок вихрових струмів. В результаті взаємодії вихрових струмів з основним струмом відбувається такий перерозподіл струму по перерізу провідника, при цьому зростає густина струму на поверхні провідника. Описане явище – поверхневий ефект- збільшується по величині при зростанні частоти струму, магнітної сприйнятності, провідності і діаметру провідника. При досить високій частоті струм протікає лише по поверхні провідника, що призводить до збільшення його активного опору R. Рис. 15. Схематичне зображення впливу на активний опір в симетричному кабелі а) б)
Ефект близькості повязаний із взаємодією зовнішніх магнітних полів Н. Так, зовнішнє поле провідника а пересікає товщину провідника б і наводить в ньому вихрові струми. На поверхні провідника б, яка ближня до поверхні провідника а, вони співпадають по напрямку з основним струмом (І + І в.с), а на протилежній поверхні – вони направлені в протилежний бік від основного струму. Аналогічний перерозподіл струмів відбувається і в провіднику а. При взаємодії вихрових струмів з основним густина результуючого струму на ближніх поверхнях провідників а і б збільшується, а на віддалених – зменшується. Це призводить до збільшення активного опору змінному струму. Ефект близькості також прямо пропорційний частоті, магнітній проникності, провідності і діаметру провідника, а також залежить від віддалі між провідниками а і б. Із зменшенням цієї віддалі дія ефекту близькості зростає в квадратній залежності від віддалі. Отже, при протіканні струму через провідники а і б в одному напрямку результуючий опір зростає, а при протилежному – зменшується.
Магнітне поле Н, створюване основним струмом, наводить вихрові струми в сусідніх провідниках кабелю, оточуючому екрані, металічній оболонці і в броні. Протікаючи по металічним частинам кабелю, вихрові струми нагрівають їх і перетворюються в теплову енергію. Крім того, вихрові струми створюють поле оберненої дії, яке впливає на провідники і змінює їх електричні параметри. Розглянемо процес передачі енергії по симетричній лінії ідеальної конструкції, тобто яка не має втрат в провідниках і без взаємодії електромагнітних полів сусідніх провідників. Розташуємо симетричну кабельну лінію вздовж осі z і скористаємось теоремою Умова – Пойтінга, згідно якої поздовжня складова вектора Пойтінга утворює з компонентами електричного Е r і магнітного Н φ полів правогвинтову систему:
Значення компонент електричного Е r і магнітного Н φ полів визначимо за допомогою рівнянь Максвелла вигляду:
Підставивши значення Н φ з другого рівняння в перше отримаємо:
Для визначення хвильового опору симетричної лінії необхідно записати закон Ома для її вибраного участка, тобто Z в = U / І. Напруга мiж провідниками лінії може бути записана через радіальну компоненту напруженості електричного поля Е r і вирахована за допомогою формули у вигляді:
Відповідно, хвильовий опір вираховується за формулою:
Для випадку без втрат в ізоляції (σ = 0) хвильовий опір Z симетричної лінії має вигляд: Маючи на увазі, що μа = 4π 10 7 μ 0 і
Первинні параметри симетричної лінії R, L, C, G (без урахування втрат – ідеальна лінія передачі сигналів) можна знайти по відомим рівнянням, які пов’язують їх з вторинними параметрами цієї лінії. Тоді отримаємо:
Для визначення втрат в реальній двохпровідній лінії необхідно знайти втрати енергії через Е z і Н φ, які входять у рівняння Умова-Пойтінга:
де R – активний опір провідника, L – внутрішня його індуктивність, Е z - поздовжня ком поненте електричного поля, а Н φ – радіальна компонента магнітного поля, r - радіус провідника. Рівняння для розрахунку опору R,Ом/км і індуктивності L, Гн/км симетричної лінії з втратами має вигляд:
де r - діаметр провідника а і б в мм; а – віддаль між провідниками в мм. Рівняння для розрахунку опору лінії складається з трьох складових: опору постійному струму Ro; опору за рахунок поверхневого ефекту R пе і опору за рахунок близькості провідників Rеб. Воно справедливе для парної скрутки. Для всіх інших конфігурацій (зіркової, подвійної парної) вираз для хвильового опору (активної нагрузки) набуває вигляд:
Величина р враховує вихрові струми: р=1- для парної срутки; р = 5 – для зіркової скрутки; p = 2 – для подвійної парної скрутки. Параметр χ вводиться для врахування ефекту cкрутки і приймає значення від 1,02 до 1,07 в залежності від діаметру кабеля. Індуктивність всієї симетричної лінії запишемо як суму зовнішньої і внутрішньої індуктивностей. Так як μ а = 4π х10-7 μо. Тоді загальний вираз має вигляд:
Для низькочастотних симетричних ліній, для яких можна не враховувати ефект близькості вирази для опору і індуктивності по спрощеним формулам мають вигляд:
Електрична ємність і провідність ізоляції симетричних ліній, які мають реальні конструкції з багатьма парами і знаходяться в металевій оболонці, розраховуються по наближеним формулам:
де χ - коефіцієнт скрутки кабельних ланцюгів (1,02…….1,07); ε - ефективна діелектрична проникність ізоляції; ψ – поправочний коефіцієнт, який характеризує близкість металічного екрану до струмопроводящих провідників. При розрахунку провідності ізоляції G необхідно враховувати недосконалість діелектрика (внутрішні вади), яка обернено пропорційна опору ізоляції лінії. Тоді загальний вираз для провідності запишеться як сума двох провідностей з урахуванням того, що провідність на змінному струмі G >> Go:
Так, для міських телефонних кабелів опір ізоляції Rizol = 2000 МОм км, а для кабелів далекого зв’язку він дорівнює 10000 МОм км. Параметри повітряних ліній зв”язку розраховуються при умові, що віддаль між провідниками більше їх радіусу (a / r ~ 50) і немає помітного викривлення магнітного поля за рахунок впливу сусідніх проводів:
Отже, параметри двохпровідної повітряної лінії можуть бути отримані як подвоєна сума однопровідної кабельної лінії. Параметри провідність G, См/км і ємність С,Ф/км повітряних ліній розраховуються аналогічним формулам для симетричних кабелів:
Температурна залежність первинних параметрів симетричної лінії в основному визначається температурною залежністю активного опору струмопровідних жил:
де α R - температурний коефіцієнт опору металу, а R20 - опір провідника при температурі 20 С.
Вторинні параметри симетричних ліній γ, Zo, α, β, υ можна виразити через параметри лінії (a,d) і електричні якості вихідних матеріалів (ε, tg δ). Підставляючи в формулу для хвильового опору Zo = √ L/C значення L і С отримаємо вираз в Oм:
Коефіцієнт затухання α симетричної лінії з мідними проводами, дБ/км має вигляд:
Підставивши в нього значення первинних параметрів, отримаємо вираз для α:
Коефіцієнт фази β рад/км визначається за формулою:
де ω- циклічна частота сигналу, с = 300000 км/с – швидкість світла в вакуумі. Швидкість розповсюдження електромагнітної хвилі вздовж симетричної лінії вимірюється в км/с і має вигляд: υ = 1/ √ LC = с/ √ ε, де ε –діелектрична проникність матеріалу ізолятора.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 392; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.236.101 (0.008 с.) |



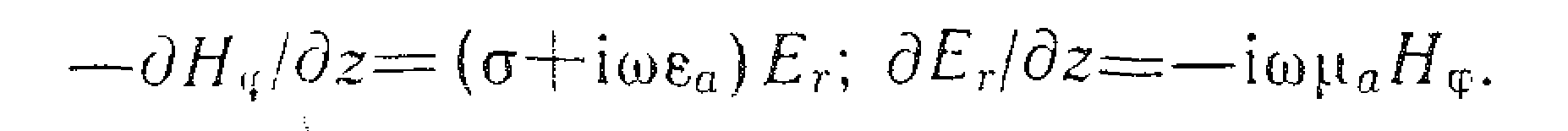



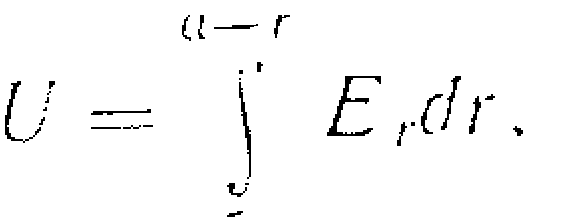 , де r - радіус провідника; а - віддаль між провідниками. Радіальну компоненту напруженості електричного поля для плоскої електромагнітної хвилі можна представити у вигляді:
, де r - радіус провідника; а - віддаль між провідниками. Радіальну компоненту напруженості електричного поля для плоскої електромагнітної хвилі можна представити у вигляді: 

 =
= отримаємо відому формулу:
отримаємо відому формулу: