
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывная и дискретная информацияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
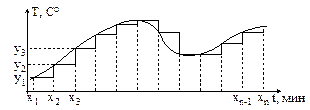
Чтобы сообщение было передано от источника к потребителю, необходима некоторая среда – носитель информации. Примерами носителей информации являются воздух для передачи речи, лист бумаги – для отсылки текста письма. Сообщение передается с помощью сигналов. В общем случае, сигнал – это физический процесс, параметры которого изменяются во времени. В данном случае во время передачи меняется параметр, характеризующий уровень сигнала, поэтому сигнал является динамическим процессом. В случае, когда параметр сигнала принимает конечное число значений, и при этом все они могут быть пронумерованы, сигнал называется дискретным. Сообщение и информация, передаваемое с помощью таких сигналов, также называются дискретными. Примером дискретной информации являются текстовая информация, так как количество символов (букв) конечно и их можно рассматривать как уровни сигнала передачи сообщения. Если параметр сигнала является непрерывной во времени функции, то сообщение и информация, передаваемая этими сигналами, называются непрерывные. Примером непрерывного сообщения является человеческая речь, передаваемая звуковой волной, с меняющейся частотой, фазой и амплитудой. Параметром сигнала в этом случае является давление, создаваемое этой волной в точке нахождения приемника – человеческого уха. Непрерывное сообщение может быть представлено непрерывной функцией, заданной на некотором отрезке [а, b]. Дискретизация – это процесс преобразования непрерывного сигнала в дискретный сигнал с некоторым шагом (частотой). Для этого диапазон значений функции (ось ординат) разбивается на конечное количество отрезков равной ширины. Тогда дискретное значение определяется отрезком, в который попало значение функции. Чем меньше шаг дискретизации, тем ближе полученный дискретный к исходному непрерывному сигналу, а, следовательно, больше точность дискретизации. Пример 2.2. На метеостанции каждые полчаса происходит замер температуры (рис. 2.1).
Рис. 2.1. Дискретизация непрерывного сообщения Непрерывно меняющаяся температура замеряется на отрезке [x1, xn]. В журнал наблюдений записывается значение температуры, округленное до целой части и являющееся дискретным значением. В данном примере получасовой промежуток является частотой дискретизации, шаг дискретизации равен 1, так как происходит округление до целого цисла, а получасовые замеры температуры – процессом дискретизации. □ Адекватность информации и ее формы Важным условием практического использования информации является ее адекватность. Адекватность информации – это уровень соответствия образа, создаваемого по информации, реальному объекту или явлению. Адекватность информации выражается в трех формах. 1. Синтаксическая адекватность – это соответствие структуры и формы представления информации без учета ее смысла. Информация в виде данных обычно обладает синтаксической адекватностью. 2. Семантическая (смысловая) адекватность в отличие от синтаксической адекватности учитывает смысловое содержание информации. 3. Прагматическая (аксиологическая, потребительская) адекватность – это соответствие ожидаемой ценности, полезности использования информации при выработке потребителем решений для достижения своей цели. Пример 2.3. Заказчик послал подрядчику сообщение: «Вышлите, пожалуйста, объем выполненных работ для отчета в течение недели». Подрядчик прислал ответ через 10 дней: «Объем выполненных работ составил 3 млн. руб.». Заказчик ожидал цифру (не график, не рисунок) и получил ее, следовательно, информация синтаксически адекватна. Полученная цифра является объемом выполненных работ, следовательно, информация семантически адекватна. Подрядчик прислал сообщение с опозданием, и ценность информации в нем потерялась, так как отчет должен был быть составлен ранее, следовательно, информация прагматически неадекватна. □ Синтаксическая мера информации Вероятностный подход Информация нуждается в измерении. На практике количество информации измеряется с точки зрения синтаксической адекватности. Исторически сложились два подхода к измерению информации: вероятностный и объемный. В 1940-х гг. К. Шеннон предложил вероятностный подход, а работы по созданию ЭВМ способствовали развитию объемного подхода. Рассмотрим вероятностный подход к измерению количества информации в соответствии с первой концепцией информации (раздел 2.1). Пусть потребитель получил в сообщении b некоторую дополнительную информацию Ib(a) о системе a, уменьшившую его первоначальную неопределенность о системе H(a) до степени Hb(a): Ib(a) = H(a) – Hb(a), то есть количество информации измеряется изменением (уменьшением) неопределенности. Мера неопределенности H(a) называется энтропией. Рассмотрим систему a, которая в каждый момент времени может принимать одно из N состояний, причем каждое из состояний равновероятно. Например, в качестве системы могут выступать опыты с подбрасыванием монеты (N = 2) или бросанием игральной кости (N = 6). Энтропия системы a вычисляется по формуле, предложенной Р. Хартли: H = H(a) = log2 N = При N = 2 энтропия минимальна и равна H = 1. Поэтому в качестве единицы информации принимается количество информации, связанное с двумя равновероятными состояниями системы, например: «орел» – «решка», «ложь» – «истина». Такая единица количества информации называется бит. Введем понятие вероятности. Вероятность события A – это отношение числа случаев M, благоприятствующих событию A, к общему количеству случаев N: P = Пример 2.4. Найти вероятность выпадения числа 6 при бросании кости. Решение. Всего граней у кости N = 6. Число 6 может выпасть M = 1.
Следовательно, вероятность выпадения числа 6 при бросании кости: P = Пример 2.5. Найти вероятность выпадения числа большего 3 при бросании кости. Решение. Всего граней у кости N = 6. Чисел больших 3 на гранях кости M = 3: 4, 5, 6.
Следовательно, вероятность выпадения числа большего 3 при бросании кости: P = Если N состояний системы неравновероятны, то есть система находится в i-м состоянии с вероятностью Pi, и при этом все состояния системы образуют полную группу событий, то есть сумма вероятностей равна 1:
то используются следующие формулы, предложенные Шенноном. Для определения количества информации в одном (i-м) состоянии системы: H = и среднего количества информации во всех состояниях системы: H = Значение количества информации для системы с N состояниями, вычисленное по формуле Хартли, будет больше, чем значение, вычисленное по формуле Шеннона. Следовательно, количество информации максимально, если состояния системы равновероятны. Пример 2.6. Вычислительная система может находиться в одном из N = 3 состояний: «включено (простой)», «вычисление», «выключено». Оператор получил сообщение о состоянии системы. Какое количество информации получил оператор? Рассмотреть два случая: 1) состояния системы равновероятны; 2) состояния системы неравновероятны; вероятность нахождения системы в состоянии «включено (простой)» P1 = 0,3; состоянии «вычисление» P2 = 0,5; состоянии «выключено» P3 = 0,2. Решение. В первом случае используем формулу Хартли: Hх = log2 N = log2 3 = 1,58 бит. Во втором случае используем формулу Шеннона: Hш = – = – (– 0,52 – 0,5 – 0,46) = 1,48 бит. □ Значение количества информации, вычисленное по формуле Хартли, больше значения, вычисленного по формуле Шеннона. Пример 2.7. В условиях задачи из примера 2.6 определить количество информации, которое получил оператор в сообщении о состоянии «выключено», вероятность которого P3 = 0,2. Решение. Используем формулу Шеннона для одного состояния: H = Можно сделать вывод, что чем событие маловероятнее, тем больше информации может быть получено при его возникновении. Объемный подход Объем данных V в сообщении измеряется количеством символов (разрядов) в этом сообщении. В информатике в основном используется двоичная система счисления, то есть все числа представляются двумя цифрами: 0 и 1. Поэтому минимальной единицей измерения данных является бит. Таким образом, 1 бит – это либо 0, либо 1. Элемент, принимающий всего два значения, называется двухпозиционным и просто реализуется аппаратно, например, двумя состояниями «включено» – «выключено», «ток есть» – «ток отсутствует». Более подробно о системах счисления будет рассказано в следующей главе. Наряду с битом используется укрупненная единица измерения – байт, равная 8 бит. Пример 2.8. Сообщение в двоичной системе счисления 10010010 имеет объем данных V = 8 бит. Этот объем данных представляется 1 байтом. □ Для удобства использования введены и более крупные единицы объема данных: 1024 байт = 1 килобайт (Кбайт); 1024 Кбайт = 1 мегабайт (Мбайт) = 10242 байт = 1048576 байт; 1024 Мбайт = 1 гигабайт (Гбайт) = 10243 байт; 1024 Гбайт = 1 терабайт (Тбайт) = 10244 байт; 1024 Тбайт = 1 пентабайт (Пбайт) = 10245 байт. Общий объем информации в книгах, цифровых и аналоговых носителях за всю историю человечества составляет по разным оценкам 1018 байт. Зато следующие 1018 байт будут созданы за следующие 5-7 лет. Отличием объема данных от количества информации заключается в следующем. Объем данных выражается только целыми значениями, а количество информации – вещественными. Формулу Хартли можно использовать для определения объема данных. При этом результат округляется в большую сторону, так как минимальной ячейкой памяти в ЭВМ является байт. Поэтому, заняв только часть байта (его несколько бит), оставшаяся часть байта остается незанятой. Пример 2.9. В сообщениях используются только первые шесть букв латинского алфавита: A, B, C, D, E, F. Сколько байт необходимо для хранения сообщения «AABBCCD»? Решение. Определим сколько бит необходимо для хранения одной буквы по формуле Хартли и округлим результат в большую сторону: VБ = log2 6 = 2,58 = 3 бита. Тремя битами можно представить 8 комбинаций: 000, 001, 010, 011, 100, 101, 110, 111. Для кодирования 6 букв используются первые шесть комбинаций, а две последние комбинации не используются. Для сообщения, состоящего из M = 7 букв, необходимо VС = M VБ = 7 × 3 = 21 бит = 2,625 байт = 3 байта. □
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.127.59 (0.006 с.) |

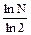 .
. .
.
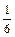 . □
. □
 =
=  . □
. □ = 1,
= 1,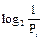 ,
, = –
= –  .
. = 2,32 бита. □
= 2,32 бита. □


