
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление символов в памяти ЭВМСодержание книги
Поиск на нашем сайте В памяти ЭВМ каждый символ (например, буква, цифра, знак препинания) закодирован в виде беззнакового целого двоичного числа. Кодировка символов – это соглашение об однозначном соответствии каждому символу одного беззнакового целого двоичного числа, называемого кодом символа. Для русского алфавита существует несколько кодировок (табл. 5.3). Таблица 5.3. Кодировки букв алфавита русского языка
В кодировках 866, 1251, КОИ-8 и Unicode первые 128 символов (цифры, заглавные и строчные латинские буквы, знаки препинания) со значениями кодов от 0 до 127 одни и те же и определяются стандартом ASCII (American Standard Code for Information Interchange – американский стандартный код для обмена информацией). Цифры 0, 1,..., 9 имеют соответственно коды 48, 49,..., 57; прописные латинские буквы A, B,..., Z (всего 26 букв) – коды 65, 66,..., 90; строчные латинские буквы a, b,..., z (всего 26 букв) – коды 97, 98,..., 122. Вторые 128 символов со значениями кодов от 128 до 255 кодировок 866, 1251, КОИ-8 содержат символы псевдографики, математические операции и символы алфавитов, отличных от латинского. Причем разные символы разных алфавитов имели один и тот же код. Например, в кодировке 1251 символ русского алфавита Б имеет тот же код, что и символ Á в стандартной кодировке ASCII. Такая неоднозначность вызывала проблемы с кодировкой текста. Поэтому была предложена двухбайтовая кодировка Unicode, которая позволяет закодировать символы многих нелатинских алфавитов. Десятичные значения кодов букв русского алфавита в кодировках 866, 1251 и Unicode приведены в табл. 5.4. Таблица 5.4. Значения кодов букв русского алфавита
В кодировке КОИ-8 (табл. 5.5) коды букв русского алфавита упорядочены не по расположению букв в алфавите, а по соответствию их буквам латинского алфавита. Например, коды латинских букв А, В, С имеют соответственно десятичные значения 65, 66, 67, а русских букв А, Б, Ц – значения 225, 226, 227. Таблица 5.5. Значения кодов букв русского алфавита
Глава 6. ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ 6.1. Алгебра высказываний. Принципы работы ЭВМ основываются на законах математической логики, поэтому ее элементы широко используются для поиска и обработки информации и при разработке схем электронных устройств. Математическая логика – это наука о формах и способах мышления и их математическом представлении. Существуют три формы мышления: 1) понятие; 2) высказывание; 3) умозаключение. Понятие объединяет совокупность объектов, обладающими некоторыми существенными признаками, которые отличают их от других объектов. Например, понятие «звезда» объединяет множество светящихся газовых шаров. Это понятие трудно спутать с таким понятием как, например, «автомобиль». Объекты, соответствующие одному понятию, образуют множество. Понятие имеет две характеристики: 1) содержание; 2) объем. Содержание понятия – это совокупность существенных признаков, выделяющих объекты, соответствующие данному понятию, среди других объектов. Например, содержание понятия «человек» можно раскрыть так: «Общественное существо, обладающее сознанием и разумом». Объем понятия «человек» определяется численностью людей, живущих в мире. Высказывание (суждение, утверждение) – это повествовательное предложение, в котором утверждаются или отрицаются свойства реальных предметов и отношения между ними. Поэтому высказывание может быть истинным или ложным. Истинным называется высказывание, в котором связь понятий правильно отражает свойства и отношения реальных вещей, например: «Москва – столица России». Истинность высказывания кодируется единицей (1) и имеет значение «истина». Ложным высказывание будет в том случае, когда оно не соответствует реальной действительности, например: «Париж – столица США». Ложность высказывания кодируется нулем (0) и имеет значение «ложь». Обычно высказывания обозначаются логическими переменными – заглавными латинскими буквами с индесом или без, например, A = «Сегодня идет дождь». Логические переменные принимают только два значения 0 и 1. Умозаключение позволяет из известных фактов (истинных высказываний) получать новые факты. Например, из факта «Все углы треугольника равны» следует истинность высказывания «Этот треугольник равносторонний». Высказывания и логические операции над ними образуют алгебру высказываний (булеву алгебру), предложенную английским математиком Джорджем Булем. Логические операции Основные логические операции над высказываниями, используемыми в ЭВМ, включают отрицание, конъюнкцию, дизъюнкции, стрелку Пирса и штрих Шеффера. Рассмотрим эти логические операции. 1. Отрицание Отрицание 2. Конъюнкция XY (X&Y, XÙY). Конъюнкция XY (AND, логическое умножение, «X и Y») – это высказывание, которое истинно только в том случае, если X истинно и Y истинно. 3. Дизъюнкция X+Y (XÚY). Дизъюнкция X+Y (OR, логическая сумма, «X или Y или оба») – это высказывание, которое ложно только в том случае, если X ложно и Y ложно. 4. Стрелка Пирса X ¯ Y. Стрелка Пирса X ¯ Y (NOR (NOT OR), ИЛИ-НЕ) – это высказывание, которое истинно только в том случае, если X ложно и Y ложно. 5. Штрих Шеффера X | Y. Штрих Шеффера X | Y (NAND (NOT AND), И-НЕ) – это высказывание, которое ложно только в том случае, если X истинно и Y истинно. Определить значения логических операций при различных сочетаниях аргументов можно из таблицы истинности (табл. 6.1) Таблица 6.1. Таблица истинности для основных логических операций, используемых в ЭВМ
Чтобы определить значение операции 0 + 1 в таблице истинности, необходимо на пересечении столбца X + Y (определяет операцию) и строки, где X = 0 и Y = 1 (так первый аргумент равен 0, а второй – 1), найти значение 1, которое и будет являться значением операции 0 + 1. В алгебре высказываний существуют две нормальные формы: конъюнктивная нормальная форма (КНФ) и дизъюнктивная нормальная форма (ДНФ). КНФ – это конъюнкция конечного числа дизъюнкций нескольких переменных или их отрицаний (произведение сумм). Например, формула X(Y + Z) находится в КНФ. ДНФ – это дизъюнкция конечного числа конъюнкций нескольких переменных или их отрицаний (сумма произведений). Например, формула X + YZ находится в ДНФ. Логические операции обладают свойствами, сформулированными в виде равносильных формул.
Правило 6.1. (порядок применения формул при преобразованиях) Перечисленные формулы рекомендуется применять в следующем порядке: 1) преобразование стрелки Пирса (6.22) и штриха Шеффера (6.23); 2) законы де Моргана (6.8)-(6.9); 3) формулы дистрибутивности (6.6)-(6.7); 4) элементарные поглощения (6.18)-(6.21). Обычно формула приводится к ДНФ, а затем отдельные слагаемые поглощаются. Логические функции
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 994; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.006 с.) |

 (обозначается также ØX, ~X).
(обозначается также ØX, ~X).
 =X. (6.1)
Коммутативность:
XY=YX. (6.2)
X+Y=Y+X. (6.3)
Ассоциативность:
(XY)Z=X(YZ). (6.4)
(X+Y)+Z=X+(Y+Z). (6.5)
Дистрибутивность:
X(Y+Z)=XY+XZ. (6.6)
X+YZ=(X+Y)(X+Z). (6.7)
Законы де Моргана:
=X. (6.1)
Коммутативность:
XY=YX. (6.2)
X+Y=Y+X. (6.3)
Ассоциативность:
(XY)Z=X(YZ). (6.4)
(X+Y)+Z=X+(Y+Z). (6.5)
Дистрибутивность:
X(Y+Z)=XY+XZ. (6.6)
X+YZ=(X+Y)(X+Z). (6.7)
Законы де Моргана:
 . (6.8)
. (6.8)
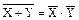 . (6.9)
Идемпотентность:
X+X=X. (6.10)
X×X=X. (6.11)
Закон противоречия:
X×
. (6.9)
Идемпотентность:
X+X=X. (6.10)
X×X=X. (6.11)
Закон противоречия:
X×  =0. (6.12)
=0. (6.12)
 . (6.22)
Преобразование штриха Шеффера:
X | Y=
. (6.22)
Преобразование штриха Шеффера:
X | Y= 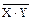 . (6.23)
. (6.23)



