
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Информация, ее виды и свойстваПонятие информации Информация, ее виды и свойства Понятие «информация» является одним из фундаментальных в современной науке вообще и базовым для информатики. Информацию наряду с веществом и энергией рассматривают в качестве важнейшей сущности мира, в котором мы живем. Однако если задаться целью формально определить понятие «информация», то сделать это будет чрезвычайно сложно. В простейшем бытовом понимании с термином «информация» обычно ассоциируются некоторые сведения, данные, знания и т. п. Информация передается в виде сообщений определяющих форму и представление передаваемой информации. Примерами сообщений является музыкальное произведение; телепередача; команды регулировщика на перекрестке; текст распечатанный на принтере; данные полученные в результате работы составленной вами программы и т. д. При этом предполагается, что имеются «источник информации» и «получатель информации». Внутренние свойства информации – это свойства, органически присущие объекту. Они обычно «скрыты» от изучающего объект и проявляют себя косвенным образом при взаимодействии данного объекта с другими. Внешние свойства, характеризующие поведение объекта при взаимодействии с другими объектами. Подобное разделение свойств можно провести и для информации. Для любой информации можно указать три объекта взаимодействия: источник информации, приемник информации (ее потребитель), и объект или явление, которые данная информация отражает. Поэтому можно выделить три группы внешних свойств, важнейшими из которых являются свойства информации с точки зрения потребителя. Качество информации – обобщенная положительная характеристика информации, отражающая степень ее полезности для пользователя. Свойства информации: релевантность, полнота, своевременность, доступность, достоверность, защищенность, эргономичность. Кроме этого информацию можно классифицировать с точки зрения ее использования на следующие виды: политическая, техническая, биологическая и т. д. Это по существу классификация по потребителю. Обобщенно характеризуя качество информации, часто используют следующее определение. Логическая, адекватно отражающая объективные закономерности природы, общества и мышления – это научная информация. Отметим, что данное определение характеризует взаимоотношение «информация – отражаемый объект/ явление» то есть это уже группа внешних свойств информации. Здесь наиболее важным является свойство адекватности. Адекватность – свойство информации однозначно соответствовать отражаемому объекту или явлению. Адекватность оказывается для потребителя внутренним свойством информации, проявляющим себя через релевантность и достоверность. Среди внутренних свойств информации важнейшими являются объем (количество) и ее внутренняя организация, структура. По способу организации информацию делят на две группы: 1.Данные или простой логически не упорядоченный набор сведений. 2.Логически упорядоченные, организованные наборы данных. Упорядоченность данных достигается наложением на данные некоторой структуры (отсюда часто используемый термин – структура данных). Остаются еще свойства, свойства связанные с процессом ее хранения. Здесь важнейшим является свойство живучесть – способность информации сохранять свое качество с течением времени. К этому еще можно добавить свойство уникальности. Уникальной называют информацию, хранящуюся в единственном экземпляре. Сообщение от источника к получателю передается по средствам какой-нибудь среды, являющейся в таком случае «каналом связи». Так, при передаче речевого сообщения в качестве канала связи можно рассматривать воздух, в котором распространяются звуковые волны, а в случае передачи письменного сообщения (например, текста, распечатанного на принтере) каналом сообщения можно считать лист бумаги, на котором напечатан текст. Человеку свойственно субъективное восприятие информации через некоторый набор ее свойств: важность, достоверность, своевременность, доступность, «больше-меньше» и т. д. Использование терминов «больше информации» или «меньше информации» подразумевает некоторую возможность ее измерения (или хотя бы количественного соотнесения). При субъективном восприятии измерение информации возможно лишь в виде установления некоторой субъективной порядковой шкалы для оценки «больше – меньше». При объективном измерении количества информации следует заведомо отрешиться от восприятия ее с точки зрения субъективных свойств, примеры которых перечислены выше. Более того, не исключено, что не всякая информация будет иметь объективно измеряемое количество. Чтобы сообщение было передано от источника к получателю, необходима материальная субстанция – носитель информации. Сообщение, передаваемое с помощью носителя, - сигнал. В общем случае сигнал – это измеряющийся во времени физический процесс. Та из характеристик процесса, которая используется для представления сообщений, называется параметром сигнала. В случае, когда параметр сигнала принимает последовательное во времени конечное число значений (при этом все они могут быть пронумерованы), сигнал называется дискретным, а сообщение, передаваемое с помощью таких сигналов, - дискретным сообщением. Если же источник вырабатывает непрерывное сообщение (соответственно параметр сигнала – непрерывная функция от времени), то соответствующая информация называется непрерывной. Примеры дискретного сообщения – текст книги, непрерывного сообщения – человеческая речь, передаваемая модулированной звуковой волной; параметром сигнала в последнем случае являться давление, создаваемое этой волной в точке нахождения приемника – человеческого уха. Непрерывное сообщение может быть представлено непрерывной функцией, заданной на некотором интервале. Непрерывное сообщение можно преобразовать в дискретное (такая процедура называется дискретизацией). Из бесконечного множества значений параметра сигнала выбирается их определенное число, которое приближенно может характеризовать остальные значения. Для этого область определения функции разбивается на отрезки равной длинны и на каждом из этих отрезков значение функции принимается постоянным и равным, например, среднему значению на этом отрезке. В итоге получим конечное множество чисел. Таким образом, любое непрерывное сообщение может быть представлено как дискретное, иначе говоря, последовательностью знаков некоторого алфавита. Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер – цифровая машина, т. е. внутреннее представление информации в нем дискретно. Дискретизация входной информации (если она непрерывна) позволяет сделать ее пригодной компьютерной обработки. Системы счисления Представление числовой информации с помощью систем счисления "Все есть число", — говорили пифагорийцы, подчеркивая необычайно важную роль чисел в практической деятельности. Известно множество способов представления чисел. В любом случае число изображается символом или группой символов (словом) некоторого алфавита. Будем называть такие символы цифрами. Для представления чисел используются непозиционные и позиционные системы счисления. Перевод чисел из одной системы счисления в другую Перевод произвольных чисел Перевод произвольных чисел, т.е. чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно — дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой (точкой). Пример 5. Перевести число 17,2510 в двоичную систему счисления.
Получаем: 17,2510=1001,012 Пример 6. Перевести число 124,2510 в восьмеричную систему.
Получаем: 124,2510=174,28 Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 2n и обратно Перевод целых чисел. Если основание q-ичной системы счисления является степенью числа 2, то перевод чисел из q-ичной системы счисления в 2-ичную и обратно можно проводить по более простым правилам. Для того, чтобы целое двоичное число записать в системе счисления с основанием q=2n, нужно: 1. Двоичное число разбить справа налево на группы по n цифр в каждой. 2. Если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов. 3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n. Пример 7. Число 1011000010001100102 переведем в восьмеричную систему счисления. Разбиваем число справа налево на триады и под каждой из них записываем соответствующую восьмеричную цифру: Получаем восьмеричное представление исходного числа: 5410628. Пример 8. Число 10000000001111100001112 переведем в шестнадцатеричную систему счисления. Разбиваем число справа налево на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
Получаем шестнадцатеричное представление исходного числа: 200F8716. Перевод дробных чисел. Для того, чтобы дробное двоичное число записать в системе счисления с основанием q=2n, нужно: 1. Двоичное число разбить слева направо на группы по n цифр в каждой. 2. Если в последней правой группе окажется меньше n разрядов, то ее надо дополнить справа нулями до нужного числа разрядов. 3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n. Пример 9. Число 0,101100012 переведем в восьмеричную систему счисления. Разбиваем число слева направо на триады и под каждой из них записываем соответствующую восьмеричную цифру:
Получаем восьмеричное представление исходного числа: 0,5428. Пример 10. Число 0,1000000000112 переведем в шестнадцатеричную систему счисления. Разбиваем число слева направо на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
Получаем шестнадцатеричное представление исходного числа: 0,80316 Перевод произвольных чисел. Для того, чтобы произвольное двоичное число записать в системе счисления с основанием q=2n, нужно: 1. Целую часть данного двоичного числа разбить справа налево, а дробную — слева направо на группы по n цифр в каждой. 2. Если в последних левой и/или правой группах окажется меньше n разрядов, то их надо дополнить слева и/или справа нулями до нужного числа разрядов; 3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n Пример 11. Число 111100101,01112 переведем в восьмеричную систему счисления. Разбиваем целую и дробную части числа на триады и под каждой из них записываем соответствующую восьмеричную цифру:
Получаем восьмеричное представление исходного числа: 745,348. Пример 12. Число 11101001000,110100102 переведем в шестнадцатеричную систему счисления. Разбиваем целую и дробную части числа на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
Получаем шестнадцатеричное представление исходного числа: 748,D216. Перевод чисел из систем счисления с основанием q=2n в двоичную систему. Для того, чтобы произвольное число, записанное в системе счисления с основанием q=2n, перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-значным эквивалентом в двоичной системе счисления. Пример 13. Переведем шестнадцатеричное число 4АС3516 в двоичную систему счисления.
Задания для самостоятельного выполнения 1. Заполните таблицу, в каждой строке которой одно и то же целое число должно быть записано в различных системах счисления.
2. Заполните таблицу, в каждой строке которой одно и то же дробное число должно быть записано в различных системах счисления.
3. Заполните таблицу, в каждой строке которой одно и то же произвольное число (число может содержать как целую, так и дробную часть) должно быть записано в различных системах счисления.
Основы логики Алгебра высказываний Алгебра в широком смысле этого слова наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и т.д.). Объектами алгебры логики являются высказывания. Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами. Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А = {Аристотель - основоположник логики} В = {На яблонях растут бананы}. Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0. Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна. Логическая операция КОНЪЮНКЦИЯ (логическое умножение): · в естественном языке соответствует союзу и; · в алгебре высказываний обозначение &; · в языках программирования обозначение And. Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение): · в естественном языке соответствует союзу или; · обозначение Ú; · в языках программирования обозначение Or. Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
Логическая операция ИНВЕРСИЯ (отрицание): · в естественном языке соответствует словам неверно, что... и частице не;
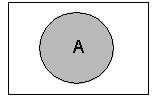
· в языках программирования обозначение Not; Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается. В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество
Логическая операция ИМПЛИКАЦИЯ (логическое следование): · в естественном языке соответствует обороту если..., то...; · обозначение Þ. Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность): · в естественном языке соответствует оборотам речи тогда и только тогда; в том и только в том случае; · обозначения Û, ~. Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Таблица истинности эквиваленции:
Логические операции имеют следующий приоритет: действия в скобках, инверсия, &, Ú, Þ, Û. Логические функции Логической (булевой) функцией называют функцию F(Х1, Х2,..., Хn), аргументы которой Х1, Х2,..., Хn (независимые переменные) и сама функция (зависимая переменная) принимают значения 0 или 1. Таблицу, показывающую, какие значения принимает логическая функция при всех сочетаниях значений ее аргументов, называют таблицей истинности логической функции. Таблица истинности логической функции n аргументов содержит 2 n строк, n столбцов значений аргументов и 1 столбец значений функции. Логические функции могут быть заданы табличным способом или аналитически — в виде соответствующих формул. Если логическая функция представлена с помощью дизъюнкций, конъюнкций и инверсий, то такая форма представления называется нормальной. Существует 16 различных логических функций от двух переменных. Таблица. Логические функции двух переменных
Пример 1. По имеющимся таблицам истинности выразите через базовые логические функции (конъюнкцию, дизъюнкцию и отрицание) следующие функции: а) F9 (X, Y) б) F15 (X, Y) Из таблицы истинности видно, что F9(X, Y) = Из таблицы истинности видно, что F15(X, Y) = Список литературы 1. Кенин А.М. Печенкина Н.С. Окно в мир компьютеров: Научно-популярное издание. Екатеринбург: Изд-во «Тезис», 1994. 2. Левин А. Самоучитель работы на компьютере. М.; 1996. 3. Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник практикум и решения. Изд-во «Лань», 1999. 4. Семененко В.А., Ступин Ю.В. Справочник по электронной вычислительной технике: Справочное пособие для профессиональных учебных заведений. М.: Машиностроение,1993. 5. Шафрин Ю.А. Основы компьютерной технологии: Учеб. Пособие для 7-11 классов по курсу «Информатика, вычислительная техника». М.; 1996.
Понятие информации Информация, ее виды и свойства Понятие «информация» является одним из фундаментальных в современной науке вообще и базовым для информатики. Информацию наряду с веществом и энергией рассматривают в качестве важнейшей сущности мира, в котором мы живем. Однако если задаться целью формально определить понятие «информация», то сделать это будет чрезвычайно сложно. В простейшем бытовом понимании с термином «информация» обычно ассоциируются некоторые сведения, данные, знания и т. п. Информация передается в виде сообщений определяющих форму и представление передаваемой информации. Примерами сообщений является музыкальное произведение; телепередача; команды регулировщика на перекрестке; текст распечатанный на принтере; данные полученные в результате работы составленной вами программы и т. д. При этом предполагается, что имеются «источник информации» и «получатель информации». Внутренние свойства информации – это свойства, органически присущие объекту. Они обычно «скрыты» от изучающего объект и проявляют себя косвенным образом при взаимодействии данного объекта с другими. Внешние свойства, характеризующие поведение объекта при взаимодействии с другими объектами. Подобное разделение свойств можно провести и для информации. Для любой информации можно указать три объекта взаимодействия: источник информации, приемник информации (ее потребитель), и объект или явление, которые данная информация отражает. Поэтому можно выделить три группы внешних свойств, важнейшими из которых являются свойства информации с точки зрения потребителя. Качество информации – обобщенная положительная характеристика информации, отражающая степень ее полезности для пользователя. Свойства информации: релевантность, полнота, своевременность, доступность, достоверность, защищенность, эргономичность. Кроме этого информацию можно классифицировать с точки зрения ее использования на следующие виды: политическая, техническая, биологическая и т. д. Это по существу классификация по потребителю. Обобщенно характеризуя качество информации, часто используют следующее определение. Логическая, адекватно отражающая объективные закономерности природы, общества и мышления – это научная информация. Отметим, что данное определение характеризует взаимоотношение «информация – отражаемый объект/ явление» то есть это уже группа внешних свойств информации. Здесь наиболее важным является свойство адекватности. Адекватность – свойство информации однозначно соответствовать отражаемому объекту или явлению. Адекватность оказывается для потребителя внутренним свойством информации, проявляющим себя через релевантность и достоверность. Среди внутренних свойств информации важнейшими являются объем (количество) и ее внутренняя организация, структура. По способу организации информацию делят на две группы: 1.Данные или простой логически не упорядоченный набор сведений. 2.Логически упорядоченные, организованные наборы данных. Упорядоченность данных достигается наложением на данные некоторой структуры (отсюда часто используемый термин – структура данных). Остаются еще свойства, свойства связанные с процессом ее хранения. Здесь важнейшим является свойство живучесть – способность информации сохранять свое качество с течением времени. К этому еще можно добавить свойство уникальности. Уникальной называют информацию, хранящуюся в единственном экземпляре. Сообщение от источника к получателю передается по средствам какой-нибудь среды, являющейся в таком случае «каналом связи». Так, при передаче речевого сообщения в качестве канала связи можно рассматривать воздух, в котором распространяются звуковые волны, а в случае передачи письменного сообщения (например, текста, распечатанного на принтере) каналом сообщения можно считать лист бумаги, на котором напечатан текст. Человеку свойственно субъективное восприятие информации через некоторый набор ее свойств: важность, достоверность, своевременность, доступность, «больше-меньше» и т. д. Использование терминов «больше информации» или «меньше информации» подразумевает некоторую возможность ее измерения (или хотя бы количественного соотнесения). При субъективном восприятии измерение информации возможно лишь в виде установления некоторой субъективной порядковой шкалы для оценки «больше – меньше». При объективном измерении количества информации следует заведомо отрешиться от восприятия ее с точки зрения субъективных свойств, примеры которых перечислены выше. Более того, не исключено, что не всякая информация будет иметь объективно измеряемое количество. Чтобы сообщение было передано от источника к получателю, необходима материальная субстанция – носитель информации. Сообщение, передаваемое с помощью носителя, - сигнал. В общем случае сигнал – это измеряющийся во времени физический процесс. Та из характеристик процесса, которая используется для представления сообщений, называется параметром сигнала. В случае, когда параметр сигнала принимает последовательное во времени конечное число значений (при этом все они могут быть пронумерованы), сигнал называется дискретным, а сообщение, передаваемое с помощью таких сигналов, - дискретным сообщением. Если же источник вырабатывает непрерывное сообщение (соответственно параметр сигнала – непрерывная функция от времени), то соответствующая информация называется непрерывной. Примеры дискретного сообщения – текст книги, непрерывного сообщения – человеческая речь, передаваемая модулированной звуковой волной; параметром сигнала в последнем случае являться давление, создаваемое этой волной в точке нахождения приемника – человеческого уха. Непрерывное сообщение может быть представлено непрерывной функцией, заданной на некотором интервале. Непрерывное сообщение можно преобразовать в дискретное (такая процедура называется дискретизацией). Из бесконечного множества значений параметра сигнала выбирается их определенное число, которое приближенно может характеризовать остальные значения. Для этого область определения функции разбивается на отрезки равной длинны и на каждом из этих отрезков значение функции принимается постоянным и равным, например, среднему значению на этом отрезке. В итоге получим конечное множество чисел. Таким образом, любое непрерывное сообщение может быть представлено как дискретное, иначе говоря, последовательностью знаков некоторого алфавита. Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер – цифровая машина, т. е. внутреннее представление информации в нем дискретно. Дискретизация входной информации (если она непрерывна) позволяет сделать ее пригодной компьютерной обработки.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.5 (0.013 с.) |
 , дополняющее его до универсального множества.
, дополняющее его до универсального множества.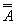
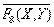 (отрицание дизъюнкции).
(отрицание дизъюнкции).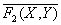 (отрицание конъюнкции).
(отрицание конъюнкции).


