
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие информатики. Количество информации по Хартли. Единицы измерения информации.Содержание книги
Поиск на нашем сайте
Понятие информатики. Количество информации по Хартли. Единицы измерения информации. А) Наука о законах и методах изменения, хранения, переработки, передачи информации с помощью математических программ и технических устройств. Б) Наука о законах и методах обработки и передачи информации с помощью компьютера. В) Область человеческой деятельности, связанная с применением компьютера.
Информация-это отражение реального мира, новые сведения которого содержаться в сообщениях. Сообщение = сумма всех сведений. Сообщение- в виде сигналов(в технике). Сигнал-это материальный носитель информации.
Количество информации по Хартли введен в 1928г. I=LOGaN I - количество информации а – число элементов алфавита N – количество сообщений N=aⁿ n-разрядность кода если a=2 I=LOG22= 1 бит-сообщение, которое может быть передано одним разрядом двоичного кода 8 бит=1 байт 1024 байт=1 кб 1024 кб=1 мб 1024 мб=1 Гб
Информационные технологии. Эволюция информационных технологий. Информационные ресурсы. Информационная система. Мультисреда, гиперсреда. Информационные технологии - совокупность методов производства процессоров и программно-технических средств объединенных в технологические цепочки, обеспечивающих сбор, хранение, выбор, обработку и распространение данных для снижения трудоемкой производственной обработки информации, повышение оперативности и надежности обработки.
Эволюция информационных технологий: -Устная передача информации -Тиражирование знаний -Использование компьютера или ЭВМ
Информационные ресурсы: Любые материальные носители информации (книги, файлы, записи, диски)
Информационная система - система предназначенная для поиска, хранения и выдачи информации по запросам пользователя.
Мультисреда - предполагает под собой совместную обработку изображений, речи, данных.Позволяет выдавать на экран изображения с текстом и звуковым сопровождением.
Гиперсреда (мультисреда – подмножество гиперсреды) - технология представляющая собой любые виды информации в виде небольших блоков, ассоциативно связанных друг с другом.
Алгоритмы с накоплением суммы.
Дано: x1, x2, x3…x10
Получит: S=∑ Xi i=1 чтобы выделит однотипные действия и организовать их повторение до определенного условия Решение: S=0, S=S+Xi, где i=1,2,3…..10
         
 
    ` `
НЕТ
Алгоритм поиска максимального элемента в массиве.


For i:= 1 to 10 begin for j:= 1 to 10 begin a[i,j]:=random(100)-50 write (a[i,j]:5); writeln; end; end.
НЕТ
Методы сортировки. 1.Перестановка 2.Выбор 3.Вставление ИДЕЯ МЕТОДОВ: Перестановка Выбор Вставление Исх.массив Исх. массив Исх. Массив
переставить найти элемент найти место
Правила и методы сортировки:
   Алгоритм отбора- первый элемент сравнивается со всеми последующими до тех пор пока не найдется элемент меньше первого(сортируем массив по возрастанию),тогда они меняются местами. Процедура повторяется до тех пор, пока не дойдет до последнего элемента. Происходит последовательная перестановка пар алгоритма, если пары расположены неправильно. Алгоритм считается завершенным, если не произошло ни одной перестановки. Алгоритм отбора- первый элемент сравнивается со всеми последующими до тех пор пока не найдется элемент меньше первого(сортируем массив по возрастанию),тогда они меняются местами. Процедура повторяется до тех пор, пока не дойдет до последнего элемента. Происходит последовательная перестановка пар алгоритма, если пары расположены неправильно. Алгоритм считается завершенным, если не произошло ни одной перестановки.
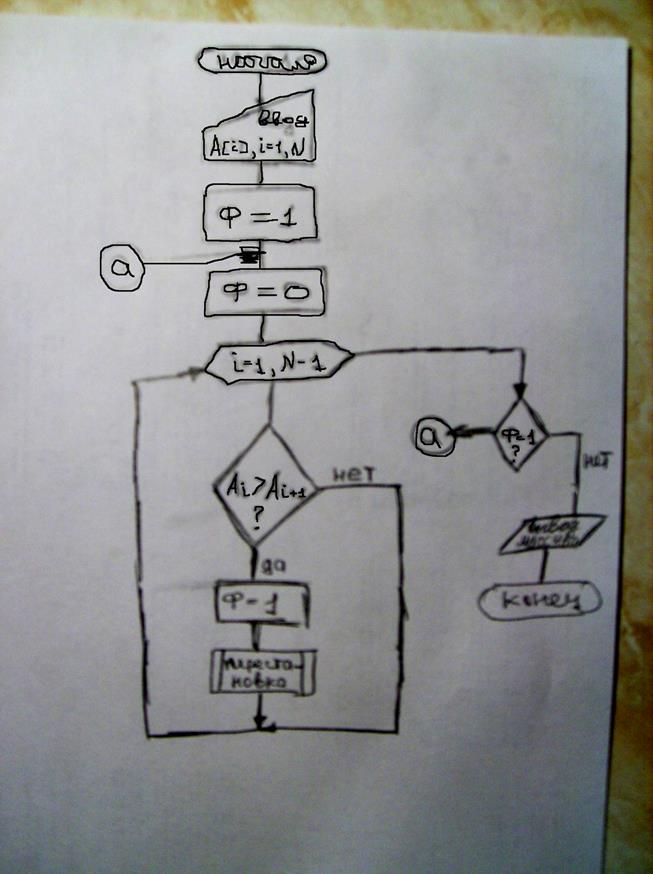
Алгоритм «ПУЗЫРЬКА»
Второй элемент сравнивается с первым элементом и если нужно то меняется с ним местами. Затем третий сравнивается со вторым, если и здесь произошла перестановка, то 2-ой элемент сравнивается с первым, то есть первые номера всплывают наверх.
Алгоритм отбора. Первый элемент сравнивается со всеми последующими пока не найдется элемент меньше первого, тогда они меняются местами. Процедура повторяется пока не дойдет до последнего элемента, затем тот же алгоритм повторяется для 2-го, 3-го и т.д. до предпоследнего элемента включительно.

Нет
да
Алгоритм замещения Происходит последовательная перестановка пар элементов массива если порядок пары не правильный. Алгоритм заканчивается если при просмотре массива не произошло ни одной перестановки.
Типы данных в языке Паскаль 1. Простой тип 2. Порядковый тип 3. Вещественный тип 4. Целочисленные типы 5. Булевские типы 6. Символьный тип 7. Перечислимые типы 8. Строковые типы 9. Структурные типы 10. Типы массив 11. Типы запись 12. Объектные типы 13. Множественные типы 14. Файловые типы 15. Ссылочные типы 16. Процедурные типы r: Real; { переменная вещественного типа } i: Integer; { переменная целого типа } c: Char; { переменная-символ } b: Boolean; { логическая переменная } e: (apple, pear, banana, orange, lemon); { переменная типа-перечисления } Цикл с параметром.(FOR) Этот вид оператора цикла называют циклом со счетчиком или циклом с параметром. В нем важную роль играет переменная-параметр, которая на каждом шаге цикла автоматически изменяет своё значение на единицу- поэтому ее и называют счетчиком. Циклы с условиями. Цикл с предусловием(while) Оператор повтора While состоит из заголовка и тела цикла. Ключевые слова while и do обозначают «до тех пор, пока» и «выполняй» соответственно. Оператор While аналогичен оператору repeat, но проверка условия выполнения цикла выполняется в самом начале оператора- если значение условия равно true(истина), то выполняются инструкции цикла, находящиеся между begin и end и снова вычисляется выражение условие выполнения цикла. Так продолжается до тех пор, пока значение Условия выполнения цикла не станет равно false (ложь). Цикл с постусловием. Оператор repeat Оператор повтора repeat состоит из заголовка (repeat), тела и условия (until). Ключевые слова repeat, until обозначают «повторяй» и «пока» соответственно. Вначале выполняется тело цикла-инструкции, которые находятся между repeat и until, затем проверяется значение условия выхода из цикла. Если оно равно false(ложь), т.е. не выполняется инструкции из цикла повторяются еще раз. Так продолжается до тех пор, пока условие не станет true (истина). Цикл с выходом из середины Цикл с выходом из середины — наиболее общая форма условного цикла. Синтаксически такой цикл оформляется с помощью трёх конструкций: начала цикла, конца цикла и команды выхода из цикла. Конструкция начала маркирует точку программы, в которой начинается тело цикла, конструкция конца — точку, где тело заканчивается. Внутри тела должна присутствовать команда выхода из цикла, при выполнении которой цикл заканчивается и управление передаётся на оператор, следующий за конструкцией конца цикла. Естественно, чтобы цикл выполнился более одного раза, команда выхода должна вызываться не безусловно, а только при выполнении условия выхода из цикла. Принципиальным отличием такого вида цикла от рассмотренных выше является то, что часть тела цикла, расположенная после начала цикла и до команды выхода, выполняется всегда (даже если условие выхода из цикла истинно при первой итерации), а часть тела цикла, находящаяся после команды выхода, не выполняется при последней итерации. Легко видеть, что с помощью цикла с выходом из середины можно легко смоделировать и цикл с предусловием (разместив команду выхода в начале тела цикла), и цикл с постусловием (разместив команду выхода в конце тела цикла). Case of и его использование Позволяет выбрать одно из нескольких возможных продолжений программы. Параметром, по которому осуществляется выбор, служит ключ выбора — переменная целого или символьного типа, или выражение любого порядкового типа (кроме REAL и STRING). Оператор выбора работает следующим образом. Вначале вычисляется значение выражения <ключ_выбора>, а затем в последовательности <констант_выбора> отыскивается такая, которая соответствует <ключу_выбора>, и выполняется <оператор>, который находится за соответствующей <константой_выбора>. Если в списке не будет найдена надлежащая константа, управление передаётся операторам, стоящим за словом ELSE. Часть ELSE <оператор> можно опускать. Тогда при отсутствии в списке нужной константы ничего не произойдёт, и оператор выбора завершит свою работу. Любому из операторов списка выбора может предшествовать не одна, а несколько констант выбора, разделённых запятыми. Функции в Паскале Функции в языке Паскаль. Описание функции на языке Паскаль имеет следующий вид: <Заголовок функции> {раздел описаний} begin {операторы функции} end; Заголовок функции имеет следующий синтаксис: function имя(список формальных параметров): тип результата; где function - служебное слово, имя - название функции- идентификатор, который формируется по тем же правилам, что и любые идентификаторы, список формальных параметров- перечень описаний формальных параметров функции (список формальных параметров может отсутствовать), тип результата- тип значения, возвращаемого функцией. Типом значения функции может быть любой простой тип. Если несколько параметров имеют один и тот же тип данных, то их можно сгруппировать и перечислить через запятую.
Примеры заголовков функций: function tg(a: real): real; function sign(a: real): integer; function ist(a, b: integer): boolean; function fam: char;
После заголовка функции следует раздел описаний, в котором описываются внутренние локальные константы, переменные, функции. За разделом описаний следует раздел операторов (тело функции), заключенный в begin... end и заканчивающийся точкой с запятой. В этом разделе обязательно должен присутствовать оператор присваивания, в левой части которого стоит имя функции - это и есть возвращаемое значение.
Вызов функции выполняется по имени с указанием в круглых скобках списка параметров. Список фактических параметров должен строго соответствовать списку формальных параметров: количество элементов в списке фактических параметров должно совпадать с количеством формальных параметров процедуры; соответствие между формальным и фактическим параметрами процедуры устанавливается по их позиции в списках; типы соответствующих элементов должны быть одинаковыми.
Вызов функции- это выражение, тип которого совпадает с типом возвращаемого функцией значения. Поэтому обращаться к функции можно в тех местах программы, где можно использовать выражения соответствующего типа. Так, если функция возвращает логическое значение, то вызов такой функции можно писать в виде условия в операторах if, while, repeat...\ until. Вызов функции можно также писать в правой части оператора присваивания, в параметрах операторов вывода. Тип записи в Паскале. Записи - структура данных, состоящая из фиксированного числа элементов определенного типаЗапись представляет собой набор элементов разных типов, каждый из которых имеет свое имя и называется полем записи. Тип записи конструируется следующим образом: record список полей1: тип1;... список полейN: типN; end type Теперь можно объявить переменные типа Date: var d1,d2: Date; Чтобы получить доступ к полям записи, следует воспользоваться точечной нотацией, указав имя переменной-записи и поле, разделенные точкой: d1.Day:=9; Как и для массивов, можно скопировать содержимое полей одной переменной-записи в другую: d2:=d1; Булева алгебра Булева алгебра. Операции отрицания, логического сложения и логического умножения. Алгебра логики — раздел математической логики, в котором изучаются логические операции над высказываниями. Высказывания могут быть истинными и ложными. Аксиомы 1. x=x, x=x; 2. x*x=0; 3. x+1=1; 4. x+x=x, x=x+x+x; 5. x+0=x; 6. x*x=x, x=x*x*x; 7. x*0=0; 8. x*1=x; 9. x+x=1. 10. x+y=x*y 11. x*y=x+y Упрощение логических формул. Законы. 1.переместительный x+y=y+x; xy=yx 2.сочетательный (x+y)+z=x+(y+z) 3.распределительный (x+y)z=xz+yz булева алгебра- boolean algebra - алгебраическая структура с тремя операциями И, ИЛИ, НЕ. Данная алгебра так названа в честь ирландца Джона Буля, который ввел ее, изучая законы логики. Булева алгебра оперирует с переменными, которые принимают два значения: "истина"= логическая единица 1, либо "ложь"= логический ноль 0. Над этими переменными выполняются операции вида: конъюнкция (И - &, *), именуемая также логическим умножением, и определяемая равенствами: 0х0 = 0, 0х1 = 0, 1х0.= 0, 1х1 = 1. дизъюнкция (ИЛИ - +, V), называемая также логическим сложением, и характеризуемая равенствами: 0+0=0, 0+1=1, 1+0=1, 1+1=1; отрицанием (НЕ – черта сверху), определяемым равенствами: не 0=1, не1=0. Операции И, ИЛИ, НЕ реализуются логическими элементами, которые являются компонентами Интегральной Схемы (ИС). Элемент выполняет одну из трех указанных выше операций либо комбинацию из этих логических операций. Например, двух операций, НЕ-И. В список логических элементов включают также триггеры и счетчики, каждый из которых выполняет более сложные логические преобразования. На булеву алгебру опираются алгебры высказываний. Здесь на основе логических операций (связок) И, ИЛИ, НЕ строятся сложные высказывания, определяющие логические выводы. Язык булевой алгебры очень удобен для описания функционирования устройств, решающих логические задачи. Сигналы и их классификация. Сигнал — это физический процесс, содержащий в себе некоторую информацию. На практике чаще всего используются электрические сигналы. При этом, носителем информации является изменяющиеся во времени ток или напряжение в электрической цепи. Сигнал - материальный носитель информации. Сигналы бывают статические и динамические (в технике). Динамические бывают непрерывными и дискретными. Дискретные бывают релейные, импульсные и цифровые (кодовые). Непрерывный сигнал – это процесс изменения некоторой физической величины во времени. Аналоговый сигнал (АС).Большинство сигналов имеют аналоговую природу, то есть изменяются непрерывно во времени и могут принимать любые значения на некотором интервале. Аналоговые сигналы описываются некоторой математической функцией времени. Аналоговые сигналы используются в телефонии, радиовещании, телевидении. Ввести такой сигнал в компьютер и обработать его невозможно, так как на любом интервале времени он имеет бесконечное множество значений, а для точного (без погрешности) представления его значения требуются числа бесконечной разрядности. Поэтому необходимо преобразовать аналоговый сигнал так, чтобы можно было представить его последовательностью чисел заданной разрядности. Дискретный сигнал. Дискретизация аналогового сигнала состоит в том, что сигнал представляется в виде последовательности значений, взятых в дискретные моменты времени. Эти значения называются отсчетами. Δt называется интервалом дискретизации. Квантованный сигнал. При квантовании вся область значений сигнала разбивается на уровни, количество которых должно быть представлено в числах заданной разрядности. Расстояния между этими уровнями называется шагом квантования Δ. Число этих уровней равно N (от 0 до N-1). Каждому уровню присваивается некоторое число. Отсчеты сигнала сравниваются с уровнями квантования и в качестве сигнала выбирается число, соответствующее некоторому уровню квантования. Каждый уровень квантования кодируется двоичным числом с n разрядами. Число уровней квантования N и число разрядов n двоичный чисел, кодирующих эти уровни, связаны соотношением n ≥ log2(N). Цифровой сигнал – содержит определенное число элементов, причем каждый из элементов может принимать только два логических значения. Логический 0 и логическая 1 могут быть выражены по разному на физическом уровне. Физические свойства сигнала, которые меняются в зависимости от логического 0 и 1 называются признаками посылок. Аналоговый дискретный квантованный цифровой
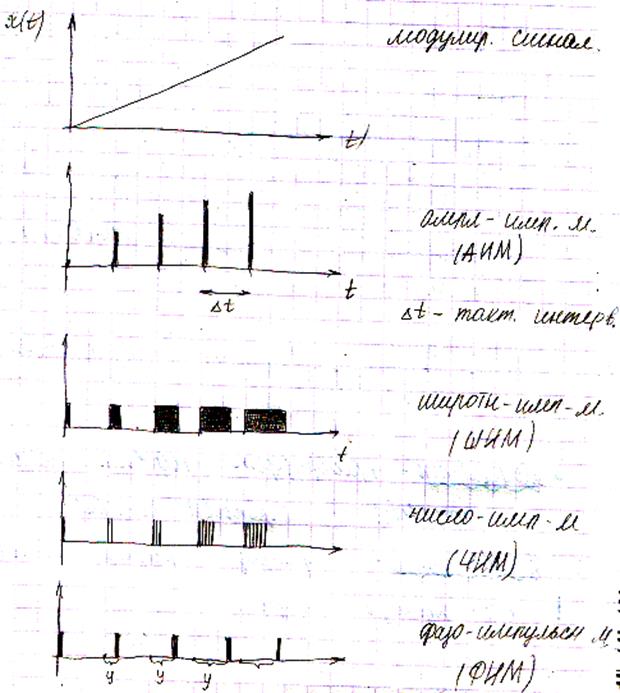
Амплитудная модуляция В линии связи - несущий сигнал. Амплитуда = const F = const
Модулирующий сигнал несет в себе полезную информацию
Виды импульсной модуляции Импульсная модуляция. Модулирующий сигнал – непрерывный. Параметры импульсов меняются по закону передаваемого сообщения. (используется в технических устройствах) Виды:
38. Назначения, характеристики, погрешность преобразования АЦП. АЦП – аналого-цифровой преобразователь. Превращает непрерывный сигнал в цифровой.
X(t) Xg(t)=N
Xi-Xi-1=Δ Ԑmax ацп=Δ Характеристики АЦП: 1.Разрядность n 2.Быстродействие преобразования (время преобразования) 3.Тип входного сигнала (U, I). 4.Диапазон входного сигнала. N – максимальное значение на выходе АЦП Ԑ – ошибка преобразования ΔԐ – интервал квантования
N=2n-1 Вход: X(t)=от 0 до 20 Ма n=4 N=2n-1=15 Ԑmax=20/15=1.3(3)мА Ԑотн в % Xmax-X0 – 100% Ԑmax - Ԑотн % Ԑотн=(1.33*100)/20=6.6% Дискретизация сигналов Дискретизация (квантование по времени) – преобразование из непрерывного в дискретный сигнал (по времени).
Δt – интервал дискретизации При вводе сигналов в компьютер сигнал проходит: А) квантование Б) дискретизацию Коды чет/нечет. Отличается от двоичного разряда добавлением контрольного разряда. В нем ставиться 1 или 0 так чтобы в сообщении было четное число элементов. Сообщение которое не соответствует этому считают недостоверным. На приемной стороне проверяется четность в принятом сообщении. Позволяет обнаружить ошибку всего лишь в одном разряде.
Нормализация чисел при записи по формату с плавающей запятой. Примеры нормализации чисел. Чтобы обеспечить однозначность представления чисел используют нормализованную форму записи:
для десятичной системы
0,125*10 –нормализованное число 12,5 *10(-1) - ненормализованное число 0,0125 – ненормализованное число Дано: А= -10110,1111 Записать А в нормализованном виде
1 1011011 0 0000101 1байт 1 байт мантисса порядок Δ = 0,00000001 - погрешность расчет конечной размерности сетки
Задача: max число по формату с плавающей запятой известна m и p.
знак числа знак порядка N2=0,111*2(111) N10=(1/2+1/4+1/8)*2(7) =(1/2+1/4+1/8)*128=0,875*128=112 2 способ: N=0,111; порядок = +7 Для записи числа в естественной форме сдвигаем запятую на 7 позиций Нормализированное число N2=1110000*20=26+25+24=64+32+16=112
Вычитание чисел
Сложение и вычитание чисел в обратном и дополнительном кодах выполняется с использованием обычного правила арифметического сложения многоразрядных чисел. Общей для этих кодов особенностью является лишь то, что при поразрядном сложении чисел разряды, изображающие знаки чисел рассматриваются как равноправные разряды двоичного числа, которые складываются друг с другом и с единицей переноса из предыдущего разряда числа по обычным правилам арифметики. Различия же обратного и дополнительного кодов связаны с тем, что делается с единицей переноса из старшего разряда (изображающего, как неоднократно говорилось, знак числа). При сложении чисел в дополнительном коде единица переноса из старшего разряда игнорируется (теряется), а в обратном коде эту единицу надо прибавить к младшему разряду результата. Пример 1. Сложить числа +12 и -5. а) В обратном коде Десятичная форма -> +12 -5 Двоичная форма -> +1100 -101 Прямой код -> 00001100 10000101 Обратный код -> 11111010 Выполним сложение в столбик: 0 0 0 0 1 1 0 0 1 1 1 1 1 0 1 0 ===============
============== 0 0 0 0 0 1 1 1 Итак, результат в обратном коде = 00000111.
Поскольку знаковый разряд равен 0, результат положительный, и, следовательно, запись кода числа совпадает с записью прямого кода. Теперь можно восстановить алгебраическую запись результата. Он равен +111 (незначащие нули отброшены), или в десятичной форме +7. Проверка (+12-5=+7) показывает, что результат верный. а) В дополнительном коде Десятичная форма -> +12 -5 Двоичная форма -> +1100 -101 Прямой код -> 00001100 10000101 Обратный код -> 11111010 +1 Дополнительный код -> 11111011
Выполним сложение в столбик: 0 0 0 0 1 1 0 0 1 1 1 1 1 0 1 1 ============ (1) 0 0 0 0 0 1 1 1
Итак, результат в дополнительном коде = 00000111. Поскольку знаковый разряд равен 0, результат положительный, и, следовательно, запись кода числа совпадает с записью прямого кода. Теперь можно восстановить алгебраическую запись результата. Он равен +111 (незначащие нули отброшены), или в десятичной форме +7. Проверка (+12-5=+7) показывает, что результат верный. Умножение и деление двоичных чисел производится в ЭВМ в прямом коде, а знаки их используются лишь для определения знака результата. Также как и в математике, умножение сводится к операциям сложения и сдвига. Деление выполняется за счет комбинирования сдвигов, вычитаний (в этот момент могут использоваться обратный или дополнительный коды) и сложений.
Понятие информатики. Количество информации по Хартли. Единицы измерения информации. А) Наука о законах и методах изменения, хранения, переработки, передачи информации с помощью математических программ и технических устройств. Б) Наука о законах и методах обработки и передачи информации с помощью компьютера. В) Область человеческой деятельности, связанная с применением компьютера.
Информация-это отражение реального мира, новые сведения которого содержаться в сообщениях. Сообщение = сумма всех сведений. Сообщение- в виде сигналов(в технике). Сигнал-это материальный носитель информации.
Количество информации по Хартли введен в 1928г. I=LOGaN I - количество информации а – число элементов алфавита N – количество сообщений N=aⁿ n-разрядность кода если a=2 I=LOG22= 1 бит-сообщение, которое может быть передано одним разрядом двоичного кода 8 бит=1 байт 1024 байт=1 кб 1024 кб=1 мб 1024 мб=1 Гб
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |






 ДА
ДА











 ДА
ДА







 ДА
ДА ДА
ДА



 НЕТ нет
НЕТ нет ДАЛЕЕ
ДАЛЕЕ

 3 3 3 1 1 1 1
3 3 3 1 1 1 1

 4 4 1 3 3 3 2
4 4 1 3 3 3 2

 5 1 4 4 4 2 3
5 1 4 4 4 2 3 1 5 5 5 2 4 4
1 5 5 5 2 4 4




 2 2 2 2 5 5 5
2 2 2 2 5 5 5


 НЕТ
НЕТ





 НЕТ
НЕТ







 ДА
ДА

 ДА НЕТ
ДА НЕТ












 АЦП РИСУНОК!!!!!!!!!
АЦП РИСУНОК!!!!!!!!!





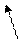 P 0 0 0 0 0 1 0 1
P 0 0 0 0 0 1 0 1

 мантисса порядок
мантисса порядок (1) 0 0 0 0 0 1 1 0
(1) 0 0 0 0 0 1 1 0 + 1 (Добавление 1 переноса)
+ 1 (Добавление 1 переноса)
 (Перенос игнорируется)
(Перенос игнорируется)


