
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Суммирование чисел по формату с фиксированной запятойСодержание книги
Поиск на нашем сайте
Сложение. С помощью двоичного сумматора по разрядам. 0+0=0 0+1=1 1+0=1 1+1=0 (и перенос единицы в старший разряд) ai+bi+Пi-1=ci+Пi ai,bi Пi-1- перенос из i-1-го разряда ci- результат в i-том разряде Пi-перенос из i–го в i+1-ый
Вычитание. Оно выполняется на том же сумматоре. А-В=А+(-B)=C Отрицательные числа при этом представляются в виде обратного или дополнительного кода. Если А,В>0 то преобразование в обратный и дополнительный код не производится. Правило получения обратного кода. Все разряды кроме знакового инвертируется при сложении по формуле +(-В) разряд переполнения не исчезает, а циклически Переносится
48-49…. Прямой код двоичного числа - это само двоичное число, в котором все цифры, изображающие его значение, записываются как в математической записи, а знак числа записывается двоичной цифрой. При этом никакого символа, отделяющего эту цифру от старшей цифры, используемой при изображении его величины, не допускается. В таких случаях говорят о том, что назначение цифры в коде определяется его позицией. Примеры.
* +1101 (+13) 0000 1101 В примерах коды * +1011101 (+93) 0101 1101 изображаются * 1101 (-13) 1000 1101 восемью цифрами
Прямой код почти не отличается от принятого в математике: для выявления абсолютной величины (модуля) числа, надо отбросить цифру, обозначающую его знак. Однако применительно к операциям сложения и вычитания такой код неудобен: правила счета для положительных и отрицательных чисел различаются. Чтобы прояснить это обстоятельство, представим что длина кода (слова) равна 5 двоичным разрядам и запишем несколько чисел в нем:
Как видно из примера, при использовании прямого кода при переходе значения число через ноль, происходит скачкообразное изменение кода! Поэтому построение устройства, в котором должны выполняться такие действия арифметики, как сложение чисел с разными знаками и вычитание, становится сложной задачей. Прямой код используется при хранении чисел в памяти ЭВМ, а также при выполнении операций умножения и деления. Чтобы построить более простые схемы АЛУ предложены и активно применяются обратный и дополнительный коды. Обратный код положительного числа совпадает с прямым, а при записи отрицательного числа все его цифры, кроме цифры, изображающей знак числа, заменяются на противоположные (0 заменяется на 1, а 1 - на 0).
Примеры записи.
* +1101 (+13) 0000 1101 В примерах коды * +1011101 (+93) 0101 1101 изображаются * 1101 (-13) 1111 0010 восемью цифрами Сопоставление этой записи с прямым кодом показывает, что непосредственно восстановить абсолютную величину (модуль) отрицательного числа непросто. Однако, в этом коде как к положительным, так и к отрицательным числам можно применять одни и те же правила, а операцию А-В можно заменить операцией сложения чисел А и “минус В”. Посмотрим, как представляется последовательные числа при переходе через ноль:
Из примера видно, что переход через ноль также не выглядит естественным. Отмеченная особенность влечет за собой и следующее - в обратном коде ноль изображают две различающиеся комбинации: 00000 (+0) и 11111 (-0), что усложняет аппаратную реализацию операций. Для восстановления прямого кода отрицательного числа из обратного кода надо все цифры, кроме цифры, изображающей знак числа, заменить на противоположные.
Дополнительный код положительного числа совпадает с прямым, а код отрицательного числа образуется как результат увеличения на 1 его обратного кода.
Иными словами, процесс построения дополнительного кода отрицательного числа можно разбить на два этапа - построить обратный код, а затем из него построить дополнительный. Проиллюстрируем это на примере. Число -> - 101101 Прямой код -> 1101101 Обратный код -> 1010010 +1 Дополнительный -> 1010011 Примеры записи.
* +1101 (+13) 0000 1101 В примерах коды * +1011101 (+93) 0101 1101 изображаются * 1101 (-13) 1111 0011 восемью цифрами В дополнительном коде, в отличие от обратного, ноль изображается только одной комбинацией, и кроме этого, достаточно естественно получается переход через ноль, если иметь в виду, что любое число, большее другого на 1, получается при прибавлении к этому другому 1 по правилам сложения. Применительно к дополнительному коду это именно так, если принять к сведению, что разрядность слова фиксирована, и единица переноса из старшего разряда теряется, поскольку ее некуда записать: 2 -> 11101 + 1 = 11110 1 -> 11110 + 1 = 11111 0 -> 11111 + 1 = (1)00000 (перенос отбрасывается) +1 -> 00000 + 1 = 00001 +2 -> 00001 + 1 = 00010
Вычитание чисел
Сложение и вычитание чисел в обратном и дополнительном кодах выполняется с использованием обычного правила арифметического сложения многоразрядных чисел. Общей для этих кодов особенностью является лишь то, что при поразрядном сложении чисел разряды, изображающие знаки чисел рассматриваются как равноправные разряды двоичного числа, которые складываются друг с другом и с единицей переноса из предыдущего разряда числа по обычным правилам арифметики. Различия же обратного и дополнительного кодов связаны с тем, что делается с единицей переноса из старшего разряда (изображающего, как неоднократно говорилось, знак числа). При сложении чисел в дополнительном коде единица переноса из старшего разряда игнорируется (теряется), а в обратном коде эту единицу надо прибавить к младшему разряду результата. Пример 1. Сложить числа +12 и -5. а) В обратном коде Десятичная форма -> +12 -5 Двоичная форма -> +1100 -101 Прямой код -> 00001100 10000101 Обратный код -> 11111010 Выполним сложение в столбик: 0 0 0 0 1 1 0 0 1 1 1 1 1 0 1 0 ===============
============== 0 0 0 0 0 1 1 1 Итак, результат в обратном коде = 00000111.
Поскольку знаковый разряд равен 0, результат положительный, и, следовательно, запись кода числа совпадает с записью прямого кода. Теперь можно восстановить алгебраическую запись результата. Он равен +111 (незначащие нули отброшены), или в десятичной форме +7. Проверка (+12-5=+7) показывает, что результат верный. а) В дополнительном коде Десятичная форма -> +12 -5 Двоичная форма -> +1100 -101 Прямой код -> 00001100 10000101 Обратный код -> 11111010 +1 Дополнительный код -> 11111011
Выполним сложение в столбик: 0 0 0 0 1 1 0 0 1 1 1 1 1 0 1 1 ============ (1) 0 0 0 0 0 1 1 1
Итак, результат в дополнительном коде = 00000111. Поскольку знаковый разряд равен 0, результат положительный, и, следовательно, запись кода числа совпадает с записью прямого кода. Теперь можно восстановить алгебраическую запись результата. Он равен +111 (незначащие нули отброшены), или в десятичной форме +7. Проверка (+12-5=+7) показывает, что результат верный. Умножение и деление двоичных чисел производится в ЭВМ в прямом коде, а знаки их используются лишь для определения знака результата. Также как и в математике, умножение сводится к операциям сложения и сдвига. Деление выполняется за счет комбинирования сдвигов, вычитаний (в этот момент могут использоваться обратный или дополнительный коды) и сложений.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

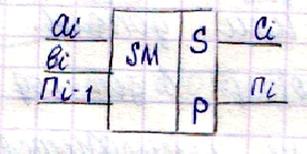 - i-ый разряд слагаемых a,b
- i-ый разряд слагаемых a,b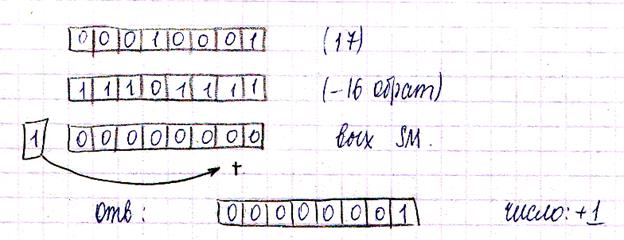

 Изображаемое число Код
Изображаемое число Код
 Изображаемое число Код
Изображаемое число Код
 Изображаемое число Код
Изображаемое число Код (1) 0 0 0 0 0 1 1 0
(1) 0 0 0 0 0 1 1 0 + 1 (Добавление 1 переноса)
+ 1 (Добавление 1 переноса)
 (Перенос игнорируется)
(Перенос игнорируется)


