Тема 6. Простые суждения и их виды (лекция) – 2 ч.

 

План:

1. Суждение как форма отражения действительности и его логическая структура.

2. Категорические суждения и их виды.

3. Модальность суждений.

 

Содержание занятия:

Суждение – форма мышления, в которой что-либо утверждается или отрицается о предметах, их признаках или об отношениях между предметами.

Суждение выражается только повествовательным предложением.

Любое суждение является истинным или ложным. Если в суждении верно отражена действительность, то оно называется истинным, в противном случае оно ложно.

Все суждения делятся так же на простые и сложные.

Простым называется суждение, не содержащее других суждений в качестве своих частей. Например, «Вода кипит при 100 °С», «Свинец тяжелее железа» и т.п. Как бы мы ни разлагали на части подобные суждения, среди полученных частей не будет такой, которая сама являлась бы суждением. Простые суждения содержат в себе лишь один субъект и один предикат, то есть одно утверждение или одно отрицание.

Различают несколько типов простых суждений.

По характеру признаков, которые утверждаются или отрицаются относительно субъектов (предметов) суждений, суждения подразделяются на:

а) атрибутивные, или сужения о свойствах. Это суждения, в которых утверждается или отрицается наличие признаков, свойств, или, иначе, атрибутов у субъекта (от лат. attributum – признак). Признаки или свойства характеризуют предметы, взятые сами по себе, вне связи с другими предметами. Это такие признаки, как цвет, форма, вес, плотность и т.д. Например: «Все воробьи – это птицы». Здесь предикат – неотъемлемый признак субъекта: быть птицей – это главный, неотъемлемый признак воробья, его атрибут.

б) релятивные, или суждения об отношениях (от лат. relativus – относительный). Это суждения, в которых утверждается или отрицается наличие у каких-либо предметов (не менее двух) отношений. Такие суждения характеризуют предметы с точки зрения их отношений, связей, взаимодействий с другими предметами: «выше», «ниже», «родственник», и т.д. и т.п. Например в суждении «Москва основана раньше Санкт-Петербурга» указывается на временнóе отношение одного города к другому.

в) экзистенциальные, или суждения существования (от лат. exsistentia – существование). Это суждения, в которых утверждается или отрицается существование или несуществование предметов, явлений и т. д. Например, «Существуют демократические государства», «Не существует идеальной демократии» и т.п. В суждениях существования не идет речь о признаках предметов как таковых (свойствах или отношениях), в них утверждается или отрицается само наличие предметов или их признаков.

Сложным называется суждение, содержащее другие суждения в качестве своих частей. Например, «Либо Лермонтов родился в Москве, либо он родился в Петербурге», «Если наступает день, становится светло» и т.п.

Логическая структура простого суждения такова: в простом суждении есть субъект, предикат, связка и квантор.

Субъект – это понятие о предмете суждения, т.е. то, о чем утверждается или отрицается в суждении. Обозначается латинской буквой S. Например, в суждении: «Все учебники являются книгами» речь идет об учебниках, поэтому его субъектом является понятие «учебники».

Предикат – понятие о признаке предмета суждения, т.е. то, что утверждается или отрицается о предмете суждения. Обозначается латинской буквой Р. В приведенном примере об учебниках утверждается, что они являются книгами, поэтому предикатом выступает понятие «книги».

Связка – это слово, соединяющее субъект и предикат суждения. В роли связки могут выступать слова «есть», «суть», «является», «это» и другие, а также тире или согласование слов, например: «Собака лает», «Дождь идет».

Перед субъектом суждения иногда стоит квантор – это указатель на объем субъекта. Он выражается словами: «все», «ни один», «некоторые». Квантор указывает относится ли суждение ко всему объему понятия, выражающего субъект, или к его части. Например, в суждении «Некоторые люди являются спортсменами» субъект «люди», предикат «спортсмены», связка «являются», а квантор слово «некоторые». Оно указывает на то, что предикат «быть спортсменами» относится только к части объема субъекта «люди».

Категорические суждения – такие суждения, в которых утверждается или отрицается принадлежность предмету свойств, состояний, видов деятельности. При этом, как уже отмечалось, в них точно установлена количественная и качественная характеристика предмета суждения.

По качеству связки («есть», «не есть») категорические суждения делятся на утвердительные и отрицательные.

По количеству предметов, о которых идет речь в суждении, они делятся на общие, частные и единичные.

Структура общего суждения: «Все S есть (не есть) Р». Например: «Все студенты сдают экзамены». В них речь идет обо всем объеме субъекта.

Структура частного суждения: «Некоторые S есть (не есть) Р». В них речь идет только о части объема субъекта.

Структура единичного суждения: «Это S есть (не есть) Р». Например: «Мурманск – областной центр». В них речь идет только об одном, уникальном субъекте.

Объединенная классификация по количеству и качеству дает 4 типа суждений:

А – общеутвердительное суждение «Все S есть Р». Например: «Все люди – позвоночные».

I – частноутвердительное суждение «Некоторые S есть Р». Например: «Некоторые студенты – двоечники».

Е – общеотрицательное суждение «Ни одно S не есть Р». Например: «Ни один дельфин не является рыбой».

О – частноотрицательное суждение «Некоторые S не есть Р». Например: «Некоторые студенты не являются отличниками».

 

Суждение

 

 

Утвердительное Отрицательное

(S есть Р) (S не есть Р)

 

А I Е О

Общее Частное Общее Частное

(Все S есть Р) (Некоторые S есть Р) (Ни одно S (Некоторые S

не есть Р) не есть Р)

 

Основная литература:

1. Гетманова А. Д. Логика: учеб. пособие для студ. вузов. - Изд. 2-е. - М.: Академический Проект, 2009. Глава 3, С. 89-103, 115-119.

2. Ивин А. А. Логика: учеб. пособие для вузов. - М.: Гардарики, 2002. Глава 6, С. 124-131, 137-147.

 

Дополнительная литература:

1. Берков В.Ф. Логика: Задачи и упражнения, Практикум. Учеб. Пособие - Мн.: НТООО "ТетраСистемс", 1998.

2. Брюшкин В.Н. Практический курс логики для гуманитариев. Учебное пособие. -М.: Новая школа, 1996.

3. Гусев Д.А. Логика: конспект лекций с задачами. – М.: Айрис-пресс, 2005.

4. Ивлев Ю.В. Логика. – М. Проспект, 2007.

5. Карпинская О.Ю., Ляшенко О.В., Меськов В.С., Шрамко Я.В. Экспресс – логика. – М.: ИНФРА-М, 1997.

Тема 7. Логические операции с простыми суждениями (практическая работа) – 2 ч.

План:

1. Отношения между субъектом и предикатом: распределенность терминов.

2. Отношение между суждениями по типу «логический квадрат».

3. Определение истинности и ложности простых суждений по их отношениям.

 

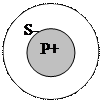
Содержание занятия:

Основные структурные элементы простого суждения – его субъект и предикат – называются терминами суждения. Термины S и Р являются либо распределенными, либо нераспределенными. Термин считается распределенным, если его объем полностью включается в объем другого термина или полностью исключается из него. Термин будет нераспределенным, если его объем частично включается в объем другого термина или частично исключается из него.

1) «Все караси – рыбы»: субъект S (караси) распределен, так как его объем полностью включен в объем предиката, предикат Р (рыбы) не распределен, так как судят только о части объема предиката (Рис.1).

 

 

Рис. 1 Рис. 2 Рис. 3 Рис. 4

2) «Все квадраты – равносторонние прямоугольники»: S и Р распределены, так как их объемы полностью совпадают (Рис. 2).

3) «Некоторые студенты – филателисты»: S не распределен, так как мыслится только часть студентов, Р тоже не распределен, так как. только некоторые филателисты являются студентами (Рис. 3).

4) «Некоторые писатели – драматурги»: S не распределен, так как мыслится только часть писателей, Р распределен, так как объем предиката полностью входит в объем субъекта (Рис.4).

5) «Ни один лев не есть травоядное животное»: объем субъекта полностью исключается из объема предиката и наоборот – S и Р распределены (Рис.5).

6) «Некоторые учащиеся не являются спортсменами»: S не распределен, так как мыслится лишь часть учащихся, а Р распределен, так как в нем мыслятся все спортсмены, ни один из которых не включен в ту часть учащихся, которая мыслится в субъекте (Рис. 6).

 

 

Рис. 5 Рис. 6

 

Простые категорические суждения видов А, I, Е, О, также как и понятия, бывают сравнимыми и несравнимыми. Сравнимые суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками, а несравнимые суждения имеют различные субъекты и предикаты. Например, суждения «Все школьники изучают математику» и «Некоторые школьники не изучают математику» являются сравнимыми. А суждения «Все школьники изучают математику» и «Некоторые спортсмены – олимпийские чемпионы» несравнимые.

Сравнимые суждения, как и понятия, бывают совместимыми и несовместимыми. Совместимыми называются суждения, которые могут быть одновременно истинными. Например: «Некоторые люди – это спортсмены» и «Некоторые люди – это не спортсмены». Несовместимыми называются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например: «Все школьники изучают математику» И «Некоторые школьники не изучают математику».

 

простые категорические суждения
сравнимые	несравнимые
совместимые	несовместимые

 

Между сравнимыми суждениями (они имеют одинаковые субъект и предикат, а различаются по количеству и (или) качеству) можно установить отношения. Отношения между ними принято схематически изображать в виде «Логического квадрата»:

 

противоположность

А Е

п п

о о

д д

ч ч

и и

н н

е е

н н

и и

е е

I частичная совместимость О

 

Суждения А и I, также как Е и О находятся в отношении логического подчинения: истинность общего суждения определяет истинность частного, подчиненного суждения. «Все студенты группы – успевающие» (подчиняющее) – «Некоторые студенты группы – успевающие» (подчиненное). Но ложность общего суждения оставляет частное суждение неопределенным. Истинность частного суждения оставляет общее суждение неопределенным. Ложность частного суждения обусловливает ложность общего суждения.

Суждения А и Е находятся в отношении противоположности: из истинности одного из противоположных суждений вытекает ложность другого, но ложность одного из них оставляет другое суждение неопределенным. Например: А - «Все люди трудятся добросовестно», Е – «Ни один человек не трудится добросовестно». Они оба ложны. Но они не могут быть оба истинными: если одно истинно, то другое ложно.

Суждения I и О находятся в отношении частичного совпадения: они имеют одинаковые субъекты и одинаковые предикаты, но различаются по качеству. Например: I - «Некоторые свидетели дают истинные показания» и О - «Некоторые свидетели не дают истинных показаний». Оба они одновременно могут быть истинными, но не могут быть одновременно ложными. Если одно из них ложно, то другое обязательно истинно. Но если одно из них истинно, то другое неопределенно (оно может быть либо истинным, либо ложным).

Суждения А и О, а также Е и I находятся в отношении противоречия. Два противоречащих суждения не могут быть одновременно истинными или одновременно ложными. Если истинно суждение I - «Некоторые летчики – космонавты», то ложным будет суждение «Ни один летчик не является космонавтом».

 

	А	I	Е	О
А	истинно	-	и	л	л
А	ложно	-	н/о	н/о	и
I	истинно	н/о	-	л	н/о
I	ложно	л	-	и	и
Е	истинно	л	л	-	и
Е	ложно	н/о	и	-	н/о
О	истинно	л	н/о	н/о	-
О	ложно	и	и	л	-

 

Основная литература:

1. Гетманова А. Д. Логика: учеб. пособие для студ. вузов. - Изд. 2-е. - М.: Академический Проект, 2009. Глава 3, С. 89-103, 115-119.

2. Ивин А. А. Логика: учеб. пособие для вузов. - М.: Гардарики, 2002. Глава 6, С. 124-131, 137-147.

Дополнительная литература:

1. Берков В.Ф. Логика: Задачи и упражнения, Практикум. Учеб. Пособие - Мн.: НТООО "ТетраСистемс", 1998.

2. Брюшкин В.Н. Практический курс логики для гуманитариев. Учебное пособие. -М.: Новая школа, 1996.

3. Гусев Д.А. Логика: конспект лекций с задачами. – М.: Айрис-пресс, 2005.

4. Ивлев Ю.В. Логика. – М. Проспект, 2007.

5. Карпинская О.Ю., Ляшенко О.В., Меськов В.С., Шрамко Я.В. Экспресс – логика. –М.: ИНФРА-М, 1997.

6. Никифоров А.Л. Общедоступная и увлекательная книга по логике, содержащая объемное и систематическое изложение этой науки профессором философии. - М.: Гнозис, Русское феноменологическое общество, 1996.

7. Рачков-Апраксин В. П. Основы логики: учеб.-метод. пособие. - Мурманск: МГПУ, 2005.

 

Темы 8-9. Сложные суждения (лекция) – 2 ч., (практическая работа) – 2 ч.

 

План:

1. Виды сложных суждений.

2. Определение истинности или ложности сложных суждений.

Содержание занятия:

Конъюнкция соответствует союзу «и». Обозначается а Ù b. (Например: «Закончилась лекция и студенты пошли домой»).

Дизъюнкция соответствует союзу «или». Обозначается а Ú b. (Например: «Он шахматист или футболист»).

Импликация соответствует союзу «если, то». Обозначается а ® b. (Например: «Если будет хорошая погода, то мы поедем за город»).

В импликативном суждении различают основание – это высказывание, идущее после слова «если», и следствие – высказывание, идущее за словом «то». «Если наступит день, то будет светло».

Эквиваленция соответствует словам «если и только если», «тогда и только тогда, когда». Обозначается а º b, или а «b. (Например: «Студенты допускаются к сдаче экзаменов тогда и только тогда, когда сдадут зачеты».)

Отрицание соответствует словам «не», «неверно, что». Обозначается ā. (Например: «падает снег» - а, «неверно, что падает снег» - ā). С помощью отрицания из данного суждения получается новое суждение, называемое отрицательным суждением. Например, из суждения «Семь – четное число» получается отрицательное суждение «Неверно, что семь – четное число». Оно складывается из исходного простого суждения и оборота «неверно, что».

Наименование	Логическая связка	Обозначение
конъюнкция	«и»	а Ù b
дизъюнкция	«или»	а Ú b
импликация	«если, то»	а ® b
эквиваленция	«если и только если»	а «b
отрицание	«неверно, что», «не»	ā

 

Любое сложное суждение является истинным или ложным в зависимости от истинности или ложности входящих в него простых суждений. Истинность или ложность сложных суждений, составленных из простых суждений (а и b) с помощью указанных логических связок, может быть выражена с помощью следующих таблиц:

а	b	а Ù b	а Ú b	а ® b	а «b
и	и	и	и	и	и
и	л	л	и	л	л
л	и	л	и	и	л
л	л	л	л	и	и

 

а	ā
и	л
л	и

 

Основная литература:

1. Гетманова А. Д. Логика: учеб. пособие для студ. вузов. - Изд. 2-е. - М.: Академический Проект, 2009. Глава 3, 103-114.

2. Ивин А. А. Логика: учеб. пособие для вузов. - М.: Гардарики, 2002. Глава 6, С. 132-137, Глава 7, С. 153-156.

 

Дополнительная литература:

1. Берков В.Ф. Логика: Задачи и упражнения, Практикум. Учеб. Пособие - Мн.: НТООО "ТетраСистемс", 1998.

2. Брюшкин В.Н. Практический курс логики для гуманитариев. Учебное пособие. -М.: Новая школа, 1996.

3. Гусев Д.А. Логика: конспект лекций с задачами. – М.: Айрис-пресс, 2005.

4. Ивлев Ю.В. Логика. – М. Проспект, 2007.

5. Карпинская О.Ю., Ляшенко О.В., Меськов В.С., Шрамко Я.В. Экспресс – логика. –М.: ИНФРА-М, 1997.

6. Никифоров А.Л. Общедоступная и увлекательная книга по логике, содержащая объемное и систематическое изложение этой науки профессором философии. - М.: Гнозис, Русское феноменологическое общество, 1996.

7. Рачков-Апраксин В. П. Основы логики: учеб.-метод. пособие. - Мурманск: МГПУ, 2005.