
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логическое (даталогическое) проектированиеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Логическое (даталогическое) проектирование — создание схемы базы данных на основе конкретной модели данных, например, реляционной модели данных. Для реляционной модели данных даталогическая модель — набор схем отношений, обычно с указанием первичных ключей, а также «связей» между отношениями, представляющих собой внешние ключи. Преобразование концептуальной модели в логическую модель, как правило, осуществляется по формальным правилам. Этот этап может быть в значительной степени автоматизирован. На этапе логического проектирования учитывается специфика конкретной модели данных, но может не учитываться специфика конкретной СУБД. Физическое проектирование Физическое проектирование — создание схемы базы данных для конкретной СУБД. Специфика конкретной СУБД может включать в себя ограничения на именование объектов базы данных, ограничения на поддерживаемые типы данных и т.п. Кроме того, специфика конкретной СУБД при физическом проектировании включает выбор решений, связанных с физической средой хранения данных (выбор методов управления дисковой памятью, разделение БД по файлам и устройствам, методов доступа к данным), создание индексов и т.д.
5. Понятие отношения в реляционной модели данных. Связи между отношениями. Определение 1. Атрибут отношения есть пара вида <Имя_атрибута: Имя_домена>. Определение 2. Отношение
Тело отношения содержит множество кортежей отношения. Каждый кортеж отношения представляет собой множество пар вида <Имя_атрибута: Значение_атрибута>:
таких что значение Отношение обычно записывается в виде:
или короче
или просто
Число атрибутов в отношении называют степенью (или -арностью) отношения. Возвращаясь к математическому понятию отношения, введенному в предыдущей главе, можно сделать следующие выводы: Вывод 1: Заголовок отношения описывает декартово произведение доменов, на котором задано отношение. Заголовок статичен, он не меняется во время работы с базой данных. Если в отношении изменены, добавлены или удалены атрибуты, то в результате получим уже другое отношение (пусть даже с прежним именем). Вывод 2: Тело отношения представляет собой набор кортежей, т.е. подмножество декартового произведения доменов. Таким образом, тело отношения собственно и является отношением в математическом смысле слова. Тело отношения может изменяться во время работы с базой данных - кортежи могут изменяться, добавляться и удаляться. 6. Реляционная модель данных. Понятие реляционный (англ. relation - отношение) связано с разработками известного американского специалиста в области систем баз данных Е. Кодда. Эти модели характеризуются простотой структуры данных, удобным для пользователя табличным представлением и возможностью использования формального аппарата алгебры отношений и реляционного исчисления для обработки данных. Реляционная модель ориентирована на организацию данных в виде двумерных таблиц. Каждая реляционная таблица представляет собой двумерный массив и обладает следующими свойствами: - каждый элемент таблицы - одни элемент данных; - все столбцы в таблице однородные, т.е. все элементы в столбце имеют одинаковый тип (числовой, символьный и тд.) и длину; - каждый столбец имеет уникальное имя; - одинаковые строки в таблице отсутствуют; - порядок следования строк и столбцов может быть произвольным. Отношения представлены в виде таблиц, строки которых соответствуют кортежам или записям, а столбцы - атрибутам отношений, доменам, полям. Поле, каждое значение которого однозначно определяет соответствующую запись, называется простым ключом (ключевым полем). Если записи однозначно определяются значениями нескольких полей, то такая таблица базы данных имеет составной ключ. 7. Теоретико-множественные операции реляционной алгебры. Объединением двух совместимых по типу отношений Объединение, как и любое отношение, не может содержать одинаковых кортежей. Поэтому, если некоторый кортеж входит и в отношение Пересечением двух совместимых по типу отношений Вычитанием двух совместимых по типу отношений
8. Специальные операции реляционной алгебры. Операция ограничения требует наличия двух операндов: ограничиваемого отношения и простого условия ограничения. Простое условие ограничения может иметь либо вид (a comp-op b), где а и b - имена атрибутов ограничиваемого отношения, для которых осмысленна операция сравнения comp-op, либо вид (a comp-op const), где a - имя атрибута ограничиваемого отношения, а const - литерально заданная константа. В результате выполнения операции ограничения производится отношение, заголовок которого совпадает с заголовком отношения-операнда, а в тело входят те кортежи отношения-операнда, для которых значением условия ограничения является true. Операция взятия проекции также требует наличия двух операндов - проецируемого отношения A и списка имен атрибутов, входящих в заголовок отношения A. Результатом проекции отношения A по списку атрибутов a1, a2,..., an является отношение, с заголовком, определяемым множеством атрибутов a1, a2,..., an, и с телом, состоящим из кортежей вида <a1:v1, a2:v2,..., an:vn> таких, что в отношении A имеется кортеж, атрибут a1 которого имеет значение v1, атрибут a2 имеет значение v2,..., атрибут an имеет значение vn. Тем самым, при выполнении операции проекции выделяется "вертикальная" вырезка отношения-операнда с естественным уничтожением потенциально возникающих кортежей-дубликатов. операция соединения (называемая также соединением по условию) требует наличия двух операндов - соединяемых отношений и третьего операнда - простого условия. Пусть соединяются отношения A и B. Как и в случае операции ограничения, условие соединения comp имеет вид либо (a comp-op b), либо (a comp-op const), где a и b - имена атрибутов отношений A и B, const - литерально заданная константа, а comp-op - допустимая в данном контексте операция сравнения. Тогда по определению результатом операции сравнения является отношение, получаемое путем выполнения операции ограничения по условию comp прямого произведения отношений A и B. Деление отношений. Эта операция наименее очевидна из всех операций реляционной алгебры и поэтому нуждается в более подробном объяснении. Пусть заданы два отношения - A с заголовком {a1, a2,..., an, b1, b2,..., bm} и B с заголовком {b1, b2,..., bm}. Будем считать, что атрибут bi отношения A и атрибут bi отношения B не только обладают одним и тем же именем, но и определены на одном и том же домене. Назовем множество атрибутов {aj} составным атрибутом a, а множество атрибутов {bj} - составным атрибутом b. После этого будем говорить о реляционном делении бинарного отношения A(a,b) на унарное отношение B(b). Результатом деления A на B является унарное отношение C(a), состоящее из кортежей v таких, что в отношении A имеются кортежи <v, w> такие, что множество значений {w} включает множество значений атрибута b в отношении B. 9. Иерархическая и сетевая модели данных. Реализация иерархических и сетевых связей в реляционной модели. Сетевая модель данных. Сетевой подход к организации данных является расширением иерархического. В сетевой структуре при тех же основных понятиях (уровень, узел, связь) каждый элемент может быть связан с любым другим элементом.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 574; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.21 (0.011 с.) |

 , определенное на множестве доменов
, определенное на множестве доменов  (не обязательно различных), содержит две части: заголовок и тело.
(не обязательно различных), содержит две части: заголовок и тело.

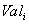 атрибута
атрибута 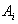 принадлежит домену
принадлежит домену 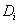
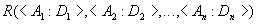 ,
, ,
,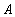 и
и 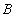 называется отношение с тем же заголовком, что и у отношений
называется отношение с тем же заголовком, что и у отношений 


