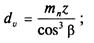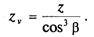Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 5. Зубчатые передачи. Косозубые и шевронные колеса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Знать устройство, принцип работы, классификацию и сравнительную характеристику зубчатых передач; особенности геометрии и расчета на прочность косозубых и шевронных зубчатых колес.
Геометрические параметры косозубых цилиндрических колес
Нормальный модуль: m = mn = Pn/π Шаг в нормальном сечении рп; окружной шаг рг.
Окружной модуль
Делительный диаметр
Диаметр вершин da = d + 2 тп; диаметр впадин df = d – 2,5тn.
Коэффициент осевого перекрытия косозубой передачи
где b — ширина венца колеса; рх — осевой шаг. Силы в зацеплении косозубой передачи
Нормальную силу Fn в зацеплении можно разложить на три составляющие (рис. 5.2, а):
где F, — окружная сила,
· При работе косозубых передач зубья входят в зацепление не сразу по всей длине, а постепенно. · Передаваемая нагрузка распределяется на несколько зубьев. · В зацеплении всегда находятся минимум две пары зубьев. · По сравнению с прямозубыми передачами повышаются нагрузочная способность, плавность и бесшумность работы. Косозубые передачи широко применяют в технике. · С увеличением угла наклона увеличиваются длина контактной линии и коэффициент перекрытия, т. е. плавность и бесшумность работы повышаются. · Одновременно увеличивается осевое усилие, дополнительно нагружающее валы и подшипники. ·
Для ограничения осевых сил угол наклона выбирают в диапазоне 8...20°, стандартные косозубые колеса изготовляют с углом β < 15°. Для уравновешивания осевых усилий применяют цилиндрические колеса с венцами, разделенными на участки с правым и левым зубом, — шевронные колеса. В шевронном колесе осевые силы на полушевронах направлены в разные стороны (рис. 5.2, б): они уравновешиваются внутри колеса и не передаются на валы и опоры. Углы наклона на шевронных колесах увеличивают до 35°, иногда больше. Недостатком шевронных колес является их высокая стоимость.
Расчет косозубых колес на контактную прочность и изгиб
Профиль косого зуба в нормальном сечении совпадает с профилем прямого зуба тп = т. В колесах с косым зубом стандартизирован нормальный модуль. При получении формул для расчета на прочность косозубого колеса используют эквивалентное прямозубое колесо, у которого форма зуба совпадает с формой зуба в нормальном сечении косозубого колеса, радиус равен радиусу кривизны эллипса, полученного в сечении п—п зуба косозубого колеса. Эквивалентное колесо изображено на рис. 5.3. Параметры эквивалентного колеса определяют по формулам: делительный диаметр
где следовательно, число зубьев
Ширина эквивалентного прямозубого колеса равна длине зуба косозубого колеса. Для расчета на прочность по контактным напряжениям и на изгиб используем формулы для прямозубого колеса. Подставив параметры эквивалентного колеса, получим формулу для проектировочного расчета передачи:
Для косозубых передач Ка = 43 МПа1/3. Косозубые передачи работают более плавно, поэтому коэффициент КHβ меньше, чем у прямозубых. Допускаемые напряжения рассчитывают так же, как для прямозубых колес. Полученное значение межосевого расстояния округляют до ближайшего стандартного значения, определяют геометрические параметры колес и проверяют полученную передачу по контактным напряжениям. Некоторые рекомендации по параметрам редукторов помещены в табл. П9 Приложения. Проверочный расчет по контактным напряжениям выполняют по формуле
где КНа, Кщ, KHv, KFa, Кп, KFv — коэффициенты нагрузки (см. расчет прямозубых передач). Если условие не выполняется, увеличивают ширину колеса b 2; если этого недостаточно, увеличивают межосевое расстояние. Проверка на изгиб Наклонное положение зубьев увеличивает их прочность на изгиб и плавность работы. Для расчета косозубых колес используют формулу для прямозубых и вводят поправочный коэффициент Yfβ — коэффициент, учитывающий наклон зуба, Yβ = 0,7...0,9. Проверку на изгиб косозубых колес выполняют по формуле
Коэффициент формы зуба YF определяют по таблицам прямозубых колес по числу зубьев эквивалентного колеса
Допускаемое напряжение [af] определяется так же, как для прямозубых колес. Для обеспечения равной прочности по контактным напряжениям и на изгиб можно определить нормальный модуль передачи по формуле
где aw — полученное при расчете по контактным напряжениям межосевое расстояние; b2 = ψbaaw.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.185.58 (0.01 с.) |

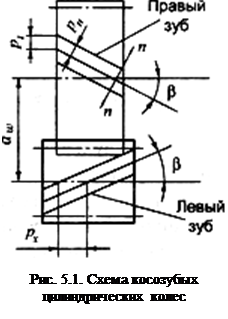 У косозубых колес зубья образуют с образующей делительного цилиндра угол β. Оси колес остаются параллельными. Зубья нарезают теми же инструментами, что и прямые зубья. У пары зубчатых колес с внешним зацеплением одинаковые углы наклона зуба, но зубья противоположно направлены. У косозубого колеса параметры измеряют в торцовом (окружном) и нормальном (п—п) направлениях (рис. 5.1).
У косозубых колес зубья образуют с образующей делительного цилиндра угол β. Оси колес остаются параллельными. Зубья нарезают теми же инструментами, что и прямые зубья. У пары зубчатых колес с внешним зацеплением одинаковые углы наклона зуба, но зубья противоположно направлены. У косозубого колеса параметры измеряют в торцовом (окружном) и нормальном (п—п) направлениях (рис. 5.1).





 Fr — радиальная сила, Fa — осевая сила,
Fr — радиальная сила, Fa — осевая сила,
 Проектировочный расчет по контактным напряжениям
Проектировочный расчет по контактным напряжениям