
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення коефіцієнта внутрішнього тертя рідини методом СтоксаСодержание книги
Поиск на нашем сайте Мета роботи:: І) вивчити механізм явища перенесення – внутрішнє тертя; 2) визначити коефіцієнт внутрішнього тертя рідини за швидкістю рівномірного падіння кульки. Прилади тa обладнання: скляний циліндр, наповнений рідиною; металеві кульки, мікрометр, секундомір.
При протіканні шарів рідини (або газу) з різними швидкостями між ними виникає тертя. Завдяки тепловому руху молекули переходять з одного шару в інший і при цьому кожна молекула переносить разом із собою імпульс свого направленого руху ( Згідно із законом Ньютона сила внутрішнього тертя F, що діє в площині дотикання двох паралельних суміжних шарів рідини (або газу), пропорційна площі їх дотикання S і градієнту швидкості
де Завдяки в'язкості тіло, що рухається в рідині, захоплює прилеглі до нього. шари і тому зазнає опору з боку рідини. Згідно із законом Стокса при невеликій швидкості руху тіла сила опору F пропорційна коефіцієнту в'язкості Для кульки з радіусом r
На кульку масою m і радіусом r, що рухається в рідині з швидкістю v діють три сили: сила опору F, сила тяжіння P та Архімедовa сила FA. Останні дві сили визначаються за формулами:
де g – прискорення вільного падіння;
При вертикальному падінні кульки в рідині сила опору, як і aрхімедовa сила, направлена вгору (рис.2). Оскільки P і FA – сталі, а сила F зростає зі збільшенням швидкості, то настане такий момент, коли буде досягнуто рівності P=FA+F. Починаючи з цього моменту, рух кульки буде рівномірним. Підставляючи в останню рівність вирази (2) – (4), маємо:
Звідси знаходимо:
або
Де d = 2 r, a l = vt – шлях, який пройшла кулька за час t.
Порядок виконання роботи 1. Вимірюють відстань l між мітками " a " і " b " циліндричної посудини, що наповнена рідиною (гліцерин, рицинова олія). 2. Мікрометром вимірюють діаметр d трьох кульок (приблизно однакових). 3. Кидають кульку в рідину так, щоб вона рухалася вздовж центральної частини циліндра; вимірюють час падіння t між мітками " a " і " b ". 4. Експериментальні дані d, l, t і табличні 5. Розраховують значення 6. Визначають відносні похибки і довірчі границі для одного з вимірювань за формулами:
Питання та вправи для самоконтролю 1. Поясніть механізм виникнення сил внутрішнього тертя. 2. Сформулюйте і запишіть закон внутрішнього тертя (закон Ньютона), дайте ілюструючий рисунок. 3. Що називається градієнтом швидкості? Який йoгo зміст? 4. Що називається коефіцієнтом внутрішнього тертя? В яких одиницях він вимірюється? Який його фізичний зміст? 5. За яких умов кулька рухається в рідині рівномірно? 6. Сформулюйте і запишіть закон Стокса.
РОБОТА 2.2 ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ПУАССОНА ГАЗУ МЕТОДОМ АДІАБАТИЧНОГО РОЗШИРЕННЯ (МЕТОД КЛЕМАНА-ДЕЗОРМА)
Мета роботи: визначити коефіцієнт Пуассона повітря і порівняти результат експерименту з висновками молекулярно-кінетичної теорії газів. Прилади та обладнання: закритий скляний балон з краном, манометр, насос. Молярною теплоємністю С будь-якої речовини називають фізичну величину, що чисельно дорівнює кількості теплоти, яку треба надати одному молю цієї речовини для підвищення його температури на один кельвін. Теплоємність газу суттєво залежить від умов, за яких надають теплоту. Так, якщо нагрівається газ при сталому об'ємі, то кількість теплоти витрачається на збільшення його внутрішньої енергії. Якщо ж газ нагрівати при сталому тиску, то він потребує ще додаткової кількості теплоти для виконання роботи при розширенні. Тому молярна теплоємність CP при сталому тиску більше молярної теплоємності при сталому об'ємі CV. Зв'язок між ними показує співвідношення Майєра:
де R – універсальна газова стала. Безпосередні виміри CP і CV здійснити важко, оскільки теплоємність газу є малою часткою теплоємності посудини, що містить газ. Легше виміряти відношення величин
де i – число ступенів свободи молекули. Коефіцієнт Пуассона γ входить до рівняння Пуассона:
яке описує зв'язок між тиском P і об'ємом V ідеального газу при адіабатичному процесі.
Метод Клемана-Дезорма для визначення відношення теплоємностей газів У скляний балон A (рис.1) за допомогою насоса накачують повітря. При швидкому накачуванні температура останнього дещо підвищується, а тому потрібно зачекати 2-3 хв для встановлення в балоні тієї ж самої температурі, що і в навколишньому середовищі. Цей стан газу будемо вважати початковим і характеризувати параметрами V 1, T 1, P 1. На рис.2 даний стан зображено точкою 1. При цьому
де Pатм – атмосферний тиск, h 1 – надлишок тиску над атмосферним. Далі відкривають кран К балона на дуже короткий проміжок часу і перекривають його у той момент, коли тиск всередині балона дорівнюватиме атмосферному. При цьому газ перейде в новий стан з параметрами V 2, T 2, Pатм (на рис.2 даний стан зображено точкою 2). Оскільки розширення повітря відбувається швидко, то можна вважати, що процес переходу газу із стану 1 у стан 2 адіабатичний. Тому для нього можна застосувати рівняння Пуассона.
Підкреслимо, що T 2< T 1 оскільки при адіабатичному розширенні газ охолоджується. Через 2-3 хв. газ нагріється до температури навколишнього повітря Т 1. При нагріванні об'єм V 2 залишається без змін, а тиск підвищується до значення
де h 2 – надлишок тиску над атмосферним після адіабатичного розширення та ізохоричного нагрівання до температури T 1. Параметри нового стану 3 позначимо через V 2, Р 2, Т 1, (на рис.2–точка 3). Істотно, що в станах 1 і 3 газ має однакову температуру, отже, стани 1 і 3 знаходяться на одній ізотермі. Тому до них можна застосувати закон Бойля - Маріотта:
Після ряду перетворень з рівнянь (1) і (2) отримаємо:
Порядок виконання роботи 1. Накачують у балон A повітря, не виходячи за поділки шкали манометра. 2. Зачекавши 2-3 хв, доки температура в балоні не стане дорівнювати температурі навколишнього повітря, відраховують покази манометра h 1. 3. Відкривши на короткий час кран К, вирівнюють тиск всередині балона з атмосферним. Коли стовпчики рідини в манометрі зрівняються, кран закривають. 4. Чекають 2-3 хв., відраховують покази манометра h 2. 5. Для кожного досліду розраховують γ за формулою (3). Повторюють дослід не менше 5 разів. 6. Результати вимірювань заносять у таблицю. 7. Визначають відносну похибку результатів вимірювань:
де 8. Розраховують довірчу границю похибок результатів вимірювань:
9. Порівнюють одержаний результат з теоретичним значенням γ повітря.
Питання і вправи для самоконтролю 1. Запишіть і сформулюйте основне рівняння молекулярно-кінетичної теорії газів. 2. Дайте визначення числа ступенів свобода тіла (системи, молекули) і виразіть молярні теплоємності ідеального газу через кількість ступенів свободи молекули. 3. Дайте визначення і отримайте вираз для внутрішньої енергії ідеального газу. 4. Запишіть і сформулюйте перший закон термодинаміки, застосуйте його до різних ізопроцесів у газах. 5. Запишіть співвідношення Майєра і поясніть фізичний зміст універсальної газової сталої. 6. Який процес називається адіабатичним? Як і чому змінюється температура газу при адіабатичній зміні його об'єму? 7. Запишіть рівняння Пуассона і поясніть зміст коефіцієнта Пуассона. Зобразіть графік адіабати.
РОБОТА 2.3
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 ). У результаті з двох суміжних шарів більш швидкий шар збагачується "повільними" молекулами, а більш повільний – "швидкими". Через це з боку шару, що рухається швидше на шар, що рухається повільніше, діє прискорююча сила, і навпаки, з боку шару, що рухається повільніше, на більш швидкий шар діє гальмуюча сила. Ці сили називають силами внутрішнього тертя, або силами в’язкості. Вони направлені по дотичній до поверхні шарів (рис 1).
). У результаті з двох суміжних шарів більш швидкий шар збагачується "повільними" молекулами, а більш повільний – "швидкими". Через це з боку шару, що рухається швидше на шар, що рухається повільніше, діє прискорююча сила, і навпаки, з боку шару, що рухається повільніше, на більш швидкий шар діє гальмуюча сила. Ці сили називають силами внутрішнього тертя, або силами в’язкості. Вони направлені по дотичній до поверхні шарів (рис 1).
 , (1)
, (1) ; v 1 і v 2 – швидкості шарів;
; v 1 і v 2 – швидкості шарів;  – відстань між шарами; знаки
– відстань між шарами; знаки  у формулі (1) відповідають гальмуючій і прискорюючій силам. Коефіцієнт пропорційності
у формулі (1) відповідають гальмуючій і прискорюючій силам. Коефіцієнт пропорційності  називається коефіцієнтом внутрішнього тертя, або коефіцієнтом в’язкості. Він чисельно дорівнює силі внутрішнього тертя, яка діє на одиницю площі дотикання шарів при градієнту швидкості, що дорівнює одиниці.
називається коефіцієнтом внутрішнього тертя, або коефіцієнтом в’язкості. Він чисельно дорівнює силі внутрішнього тертя, яка діє на одиницю площі дотикання шарів при градієнту швидкості, що дорівнює одиниці. , швидкості тіла v та його лінійним розмірам l:
, швидкості тіла v та його лінійним розмірам l: 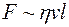 .
. . (2)
. (2) ; (3)
; (3) , (4)
, (4) – густина кульки;
– густина кульки; 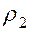 – густина рідини.
– густина рідини.
 .
. ,
, (5)
(5) і
і  заносять у таблицю.
заносять у таблицю. ;
; ;
;  .
.
 ,
, , яке називають коефіцієнтом Пуассона. Виходячи з уявлень класичної молекулярно-кінетичної теорії, можна показати, що для ідеального газу
, яке називають коефіцієнтом Пуассона. Виходячи з уявлень класичної молекулярно-кінетичної теорії, можна показати, що для ідеального газу ,
,

 базується на використанні методу адіабатичного розширення. Адіабатичним називається процес, який відбувається без теплообміну системи з навколишнім середовищем. Адіабатичний процес можна здійснити або за допомогою теплової ізоляції системи, або за умову короткочасності процесу (за малий проміжок часу не встигає відбутися тепловий обмін з навколишнім середовищем).
базується на використанні методу адіабатичного розширення. Адіабатичним називається процес, який відбувається без теплообміну системи з навколишнім середовищем. Адіабатичний процес можна здійснити або за допомогою теплової ізоляції системи, або за умову короткочасності процесу (за малий проміжок часу не встигає відбутися тепловий обмін з навколишнім середовищем). ,
, ;
;  . (1)
. (1) ,
, ;
;  . (2)
. (2) .
. ,
,  ,
, , c - ціна поділки шкали манометра.
, c - ціна поділки шкали манометра. .
.


