
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Циклограмма работы кулачкового механизмаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рис. 2 Большинство кулачковых механизмов относится к цикловым механизмам с периодом цикла равным 2p. В цикле движения толкателя в общем случае можно выделить четыре фазы (рис. 2): удаления из самого близкого (по отношению к центру вращения кулачка) в самое дальнее положение, дальнего стояния (или выстоя в самом дальнем положении), возвращения из самого дальнего положения в самое близкое и ближнего стояния (выстоя в самом ближнем положении). В соответствии с этим, углы поворота кулачка или фазовые углы делятся на:
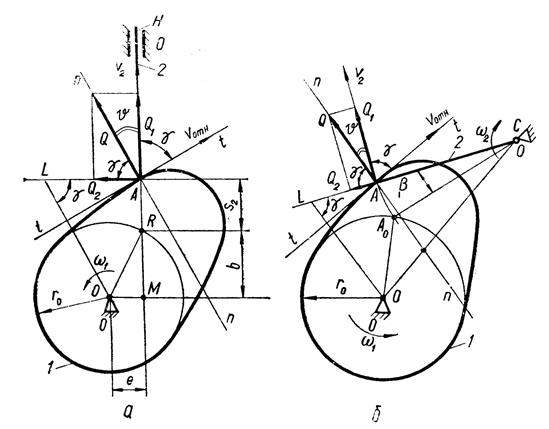
Сумму φу + φд + φв называют рабочим углом и обозначают φр. Следовательно, φу + φд + φв = φр. Угол давления и угол передачи движения Угол давления ϑ определяет положение нормали п-п в высшей КП относительно вектора скорости и контактной точки ведомого звена (рис. 3, а, б). Его величина определяется размерами механизма, передаточной функцией Угол передачи движения γ - угол между векторами υ2 и υотн абсолютной и относительной (по отношению к кулачку) скоростей той точки толкателя, которая находится в точке контакта А (рис. 3, а, б):
Если пренебречь силой трения между кулачком и толкателем, то силой, приводящей в движение толкатель (движущей силой), является давление Q кулачка, приложенное к толкателю в точке А и направленное по общей нормали п-п к профилям кулачка и толкателя. Разложим силу Q на взаимно перпендикулярные составляющие Q1 и Q 2, из которых первая направлена по направлению скорости υ2. Сила Q1 перемещает толкатель, преодолевая при этом все полезные (связанные с выполнением технологических задач) и вредные (силы трения) сопротивления, приложенные к толкателю. Сила Q2 увеличивает силы трения в кинематической паре, образованной толкателем и стойкой. Очевидно, что с уменьшением угла γ сила Q1 уменьшается, а сила Q 2 увеличивается. При некотором значении угла γ может оказаться, что сила Q1 не сможет преодолеть все сопротивления, приложенные к толкателю, и механизм не будет работать. Такое явление называют заклиниванием механизма, а угол γ, при котором оно имеет место, называют углом заклинивания γзакл. При проектировании кулачкового механизма задают допускаемое значение угла давления ϑдоп, обеспечивающее выполнения условия γ ≥ γ min > γ закл, т. е. текущий угол γ ни в одном положении кулачкового механизма не должен быть меньше минимального угла передачи γ m in и значительно превосходить угол заклинивания γзакл . Для кулачковых механизмов с поступательно движущимся толкателем рекомендуется γ min = 60° (рис. 3, а)и γmin = 45° - механизмов с вращающимся толкателем (рис. 3, б).
Рис. 3 Графическое интегрирование При проектировании кулачковых механизмов закон движения толкателя обычно задается в виде функциональной зависимости аналога ускорения толкателя от угла поворота кулачка: При ω1 = const имеют место такие соотношения:
если толкатель перемещается прямолинейно (рис. 3, а); если же толкатель колеблется вокруг неподвижной оси (рис. 3, б), то
Для построения профиля кулачка достаточно иметь зависимости S = S (t) или ψ = ψ (t). Поэтому в указанных случаях приходится дважды интегрировать заданные зависимости. На рис. 4представлена кривая у" = у" (x), выражающая, в зависимости от типа кулачкового механизма, либо
Рис. 4 Площади F1 и F2, а также F’2 и F’1 должны быть равны между собой, поскольку скорость толкателя в начале и конце углов удаления и возвращения равна нулю. Проинтегрируем дважды графически заданную зависимость. Для этого: 1) построим ординаты ab, cd,..., соответствующие серединам интервалов 01, 12,..., и отложим отрезки Ob'= ab, Od' = cd на оси ординат; 2) соединим произвольно взятую точку Р 1 на продолжении оси х с точками b', d',...; 3) на рис. 4, б из точки О 1 проводим отрезок О1b" в интервале О11 параллельно лучу Р1b', отрезок b"d" в интервале 1—2 параллельно лучу P1d' и т.д. Полученная ломаная линия (в пределе — кривая) в графической форме представляет собой первый интеграл заданной зависимости, т. е. кривую у' — у' (х) и, значит, с учетом масштабов, либо Аналогично, интегрируя кривую у' = у' (х), получаем вторую интегральную кривую у = у (х), с учетом масштабов S=S(φ) (рис. 4, в), либо ψ = ψ(φ). Для определения произвольных постоянных интегрирования приходится задаваться некоторыми начальными условиями. В дальнейшем будем полагать, что в нижнем положении толкателя его скорость (линейная либо угловая) должна равняться нулю. Естественно также начало отсчета времени t относить к этому моменту. Таким образом, получаем следующие начальные условия для кулачковых механизмов: а) с поступательно движущимся толкателем t0 = 0; V0= 0; S0 = 0; б) с вращающимся толкателем t0 = 0; ωT=0; ψ0 = ψmin.
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 953; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |


 и перемещения толкателя S .
и перемещения толкателя S . .
.
 - для механизмов с поступательно движущимся толкателем или
- для механизмов с поступательно движущимся толкателем или 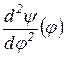 - для механизмов с вращающимся толкателем, так как для обеспечения режима технологического процесса к закону изменения скорости или ускорения толкателя часто предъявляются определенные требования.
- для механизмов с вращающимся толкателем, так как для обеспечения режима технологического процесса к закону изменения скорости или ускорения толкателя часто предъявляются определенные требования.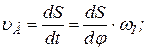 (1)
(1)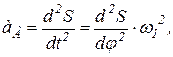 (2)
(2) (3)
(3)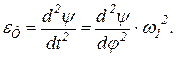 (4)
(4) либо
либо 


 либо
либо 



