
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рекомендуемые масштабы величинСодержание книги Поиск на нашем сайте
Пусть по оси x (рис. 4) отложен отрезок длиной L мм, представляющий собой угол поворота кулачка, равный 2π (или 3600). В этом случае масштаб углов поворота
либо
При принятом нами законе движения φ = ω1 t из последних равенств можно определить масштаб времени, если на оси x откладывать не углы поворота φ кулачка, а соответствующие им значения времени. Тогда
отсюда
Т. о., масштабы времени и углов поворота кулачка определяются выбранной величиной отрезка L (это и понятно), представляющего собой один оборот кулачка (либо один период его вращения). Так как обычно при исследовании движения период делится на l равных частей, где l для удобства вычерчивания принимается кратным 12, то, очевидно, и отрезок, равный L мм, выгодно брать также кратным 12. Поэтому в зависимости от величины вычерчиваемой диаграммы можно рекомендовать значения L = 120, 180, 240, 300, 360 мм. Пример. L = 360 мм. Тогда При этом масштаб времени μt будет: Из приведенных формул видно, что масштабы μφ и μt обратно пропорциональны длине L. Поэтому, уменьшая в предыдущем примере значение L в 2, 3, 4,…, k раз, тем самым увеличиваем соответствующим образом значения масштабов μφ и μt. Например, при L = 180 мм будем иметь
Зависимость между масштабами линейных и угловых путей, скоростей и ускорений толкателя при графическом интегрировании Поступательное перемещение ведомого звена (толкателя). Из курса теории механизмов известно, что между масштабами диаграмм при графическом интегрировании существуют такие зависимости (рис. 4):
В заданиях на проект закон движения толкателя дается в форме кривой Масштабы обеих кривых связаны равенством (6), но в нем неизвестными являются значения Н1, Для того чтобы построенные диаграммы были удобочитаемыми, следует обеспечить такие значения ординат Вращение вокруг неподвижной оси ведомого звена (коромысла). В этом случае вместо диаграммы
Значения H1 и H2 выбирают здесь в пределах 40—60 мм. Максимальный угол поворота коромысла βmax задается. Поэтому и здесь масштаб μψ находится так:
После этого определяют масштабы Зная масштабы всех кинематических диаграмм, можно определить значения пройденного пути, скорости и ускорения толкателя
Пример. Определить максимальное значение ускорения толкателя при заданных диаграмме аналога ускорения (рис. 5) и частоты вращения кулачка Решение. По графику зависимости аналога ускорения толкателя от угла поворота кулачка (рис. 5) измеряем максимальную ординату
где Симметричные и несимметричные кинематические диаграммы Толкателя. На рис. 4, а кривая на участке φу - φд - φв имеет ось симметрии ММ,параллельную оси ординат и делящую, следовательно, этот отрезок абсциссы пополам. При таком задании, очевидно, должны иметь место следующие условия: площади F1 = F1’ и F2 = F2’. Вместе с тем, по абсолютной величине должны равняться между собой площади: F1 = |F2 |; |F2’| = F1’,так как по условиям работы скорость толкателя как в начале и конце подъема, так в начале и в конце опускания должны равняться нулю. По аналогичным соображениям имеет место и равенство: F3 = |F4|,так каквеличина подъема толкателя должна быть равна величине его опускания за время одного периода. Из этого следует, что в симметричных диаграммах угол φу поворота кулачка, соответствующий полному подъему толкателя, должен быть равен углу φв поворота кулачка, соответствующему возвращению толкателя из верхнего (дальнего) положения в нижнее (ближнее): φу = φв. Однако очень часто приходится проектировать кулачковые механизмы, в которых φу ≠ φв. Это имеет место в тех случаях, когда подъем толкателя, например, соответствует рабочему ходу, а опускание — холостому (или наоборот). Естественно, что на холостой ход желательно тратить меньше времени, и, следовательно, соответствующий ему угол поворота кулачка следует брать как можно меньше. Несимметричные диаграммы приходится строить в двойном масштабе, так как площади F1 ≠ F1’ и F2 ≠ F2’. Само собой разумеется, что применение двойных масштабов к кинематическим диаграммам является неудобным и трудоемким. Существует способ, позволяющий построить всю диаграмму в одном масштабе в случае, когда φу ≠ φв и получить, следовательно, на следующей диаграмме F3 = — F4,а значит, и у1 = у2. Таким образом, можно избежать неудобства применения двух масштабов. Этот способ справедлив, однако, лишь в тех случаях, когда оба участка диаграммы (рис. 5)заданы одноименными кривыми. Способ состоит в том, что наибольшие ординаты h’ и h" обоих участков диаграммы
Рис. 5
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.214.244 (0.006 с.) |

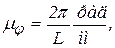
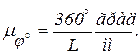

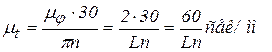
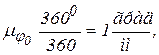 или
или 
 где n – число оборотов в минуту кулачка.
где n – число оборотов в минуту кулачка. или
или  .
. (5)
(5) (6)
(6) без указания масштабов, в которых эта кривая построена. Интегрируя эту кривую, получаем кривую
без указания масштабов, в которых эта кривая построена. Интегрируя эту кривую, получаем кривую 
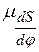 и
и 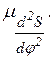
 и
и  ,которые были бы достаточно большими и вместе с тем не выходили за пределы участков, отведенных для этих диаграмм на чертеже. Например, можно рекомендовать для ординаты
,которые были бы достаточно большими и вместе с тем не выходили за пределы участков, отведенных для этих диаграмм на чертеже. Например, можно рекомендовать для ординаты  отрезок y"mаx,равный 60—80 мм. Значения
отрезок y"mаx,равный 60—80 мм. Значения  (рис. 3). Определив, таким образом, μ s, можно затем по равенствам (5) и (6) найти
(рис. 3). Определив, таким образом, μ s, можно затем по равенствам (5) и (6) найти  в заданиях на проект дается диаграмма
в заданиях на проект дается диаграмма  Интегрируя ее последовательно дважды, получаем кривые
Интегрируя ее последовательно дважды, получаем кривые  и ψ – φ, масштабы которых связаны между собой так:
и ψ – φ, масштабы которых связаны между собой так: (5, a)
(5, a) (6, а)
(6, а)
 и
и  из равенств (5, а) и (6, а).
из равенств (5, а) и (6, а). в любом положении механизма.
в любом положении механизма.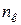 .
.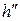 в миллиметрах и подставляем в формулу:
в миллиметрах и подставляем в формулу: ,
, .
. берутся в отношении, обратно пропорциональном квадратам углов φу и φв, т. е.
берутся в отношении, обратно пропорциональном квадратам углов φу и φв, т. е. или
или  .
.



