
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамический синтез кулачковых механизмов типа IIСодержание книги
Поиск на нашем сайте
Заданы длина l толкателя, допускаемый угол давления Задачей динамического синтеза в данном случае является определение такого минимального радиус-вектора r0 профиля кулачка и такого расстояния d между центрами вращения кулачка и толкателя, при наличии которых переменный угол передачи движения γ ни в одном положении кулачкового механизма не будет меньше Построения, связанные с динамическим синтезом, приведены на рис. 7. Точка С — центр вращения толкателя. Дуга SR радиуса l является ходом толкателя Технические приемы разметки следующие. 1. На дуге SR отметить точку А0 -начальное положение толкателя (самое ближнее к центру вращения кулачка). Продолжить луч СА0 на произвольный отрезок А0К0 (на рис. не показано). 2. От точки К0 восстановить перпендикуляр и на нем отложить отрезки К0К1 = СК0 tgβ1, К0К2= СК0 tgβ2 ,..., К0Кi = СК0 tgβi. Значения углов поворота толкателя определяем по диаграмме ψ – φ: 3. Из центра вращения толкателя С проводим лучи через полученные точки К1 К2 …Кi и на пересечении этих лучей с дугой SR получаем точки А1, А2,…, Аi. От точек деления Аi дуги SR на лучах СА0; СА1 и т. д откладываем отрезки AiLi’ и AiLi’’, изображающие в масштабе μs величину
Рис. 7
Поместим центр вращения кулачка в точке О, находящейся внутри области RDN. Тогда отрезок ОА0 определяет минимальный радиус r0 кулачка, а отрезок ОС — расстояние d между центрами вращения толкателя и кулачка. Чем дальше от точки О внутри области RDN находится центр вращения кулачка, тем лучше становятся условия работы механизма, так как углы γ увеличиваются. Однако при этом размеры механизма также увеличиваются, так как возрастает минимальный радиус r0 кулачка и расстояние d. Динамический синтез кулачкового механизма типа III Для осуществления динамического синтеза кулачковых механизмов типа III (рис. 1, в),у которых элемент выходного звена прямая α-α образует с направлением движения звена 2 постоянный угол передачи γ = 90°, необходимо выполнения дополнительного условия. Это условие заключается в том, чтобы профиль кулачка был всегда выпуклым, так как его профиль есть огибающая кривая к положениям прямой α-α. Условие будет выполняться, если значения суммы минимального радиуса rmin кулачка и перемещения S толкателя 2 в каждом положении будут больше аналога ускорения, взятом со знаком минус:
Существует два способа графического определения минимального радиуса rmin кулачка. Первый способ (метод Я. Л. Геронимуса). 1. Из диаграмм S(φ) и
Полученная кривая
Рис. 8
2. Проводим касательную АВ к той части кривой, которая лежит во втором квадранте, под углом 45° к оси S. Несколько увеличенный отрезок ОВ с учетом масштаба является минимальным радиусом кулачка
Второй способ. Из неравенства (7) следует, что Отсюда вытекает такой способ определения: r min = S min. Наложим диаграммы (S — φ) и
На рис. 9 приводится уже просуммированная диаграмма при γ = 90°. Заметим, что rmin = Smin всегда больше нуля и поэтому приведенное выше неравенство показывает, что rmin должно быть больше наибольшей отрицательной ординаты, полученной при наложении диаграмм. Это обеспечивает существование приведенного неравенства во всех положениях механизма. Обозначим наибольшее абсолютное значение отрицательной ординаты через a. Тогда, гарантируя «запас», берем с некоторым увеличением найденное значение, а именно: rmin = Smin = (a + δ) μS,
где δ определяется из равенства δμS ≈ 10 мм.
Рис. 9
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.59.124 (0.01 с.) |

 и направление вращения кулачка. Вращение кулачка направлено по часовой стрелке.
и направление вращения кулачка. Вращение кулачка направлено по часовой стрелке. .
. . Эта дуга размечена в соответствии с осью ординат диаграммы s2 – φ1.
. Эта дуга размечена в соответствии с осью ординат диаграммы s2 – φ1. .
.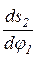 ,причем направление отрезков определяется поворотом вектора скорости точки А толкателя на 90° в сторону вращения кулачка. Через концы этих отрезков проводим прямые, образующие с соответствующими лучами углы γmin. Получаем два семейства прямых: прямые первого семейства начинаются в точках Li’ и идут слева направо (если смотреть с концов прямых к точкам Li’); прямые второго семейства начинаются в точках Li’’ и идут справа налево. Часть плоскости RDN, ограниченная пересечением двух кривых QDN и RDT, из которых первая сгибает крайние левые прямые первого семейства, а вторая — крайние правые прямые второго семейства, определяет геометрическое место точек, каждую из которых можно принять за центр вращения кулачка, причем при таком выборе угол передачи движения γ ни в одном положении не будет меньше γmin.
,причем направление отрезков определяется поворотом вектора скорости точки А толкателя на 90° в сторону вращения кулачка. Через концы этих отрезков проводим прямые, образующие с соответствующими лучами углы γmin. Получаем два семейства прямых: прямые первого семейства начинаются в точках Li’ и идут слева направо (если смотреть с концов прямых к точкам Li’); прямые второго семейства начинаются в точках Li’’ и идут справа налево. Часть плоскости RDN, ограниченная пересечением двух кривых QDN и RDT, из которых первая сгибает крайние левые прямые первого семейства, а вторая — крайние правые прямые второго семейства, определяет геометрическое место точек, каждую из которых можно принять за центр вращения кулачка, причем при таком выборе угол передачи движения γ ни в одном положении не будет меньше γmin.
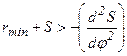 . (7)
. (7) исключается графически параметр φ. При этом на получаемой диаграмме
исключается графически параметр φ. При этом на получаемой диаграмме  (рис. 8)масштабы на обеих осях должны быть между собой равны:
(рис. 8)масштабы на обеих осях должны быть между собой равны: .
. (рис. 8) расположится в первом и втором квадрантах координатной системы.
(рис. 8) расположится в первом и втором квадрантах координатной системы.
 .
.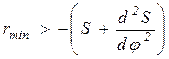
 (рис. 9) одну на другую и просуммируем их. Разумеется, для этого необходимо предварительно вычертить их в одном масштабе, т. е. нужно, чтобы
(рис. 9) одну на другую и просуммируем их. Разумеется, для этого необходимо предварительно вычертить их в одном масштабе, т. е. нужно, чтобы




