
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
О.А. Шипилова, Н.И. Миндиярова, Е.Ю. МосквинаСодержание книги Поиск на нашем сайте
О.А. Шипилова, Н.И. Миндиярова, Е.Ю. Москвина
Проектирование Кулачковых механизмов
учебно-методическое пособие по курсовому проектированию по дисциплине «Теория механизмов и машин» для студентов специальностей 151001 «Технология машиностроения», 130602 «Машины и оборудование нефтяных и газовых промыслов» очной, заочной и очно-заочной форм обучения
Альметьевск 2009 УДК 621.01 Ш 63 О.А. Шипилова, Н.И. Миндиярова, Е.Ю. Москвина. Ш 63 Проектирование кулачковых механизмов: у чебно-методическое пособие по курсовому проектированию по дисциплине «Теория механизмов и машин» для студентов специальностей 151001 «Технология машиностроения», 130602 «Машины и оборудование нефтяных и газовых промыслов» очной, заочной и очно-заочной форм обучения. – Альметьевск: Альметьевский государственный нефтяной институт, 2009. – 36 с.
В методическом пособии «Проектирование кулачковых механизмов» приведены общие сведения о кулачковых механизмах и критерии их работоспособности. Изложен метод графического интегрирования. Дана методика решения задач динамического и кинематического синтеза кулачковых механизмов трех типов. Печатается по решению учебно-методического совета АГНИ.
Рецензенты: Доцент кафедры «НГО», к.т.н. Бикбулатова Г.И. Инженер «СМП-Нефтегаз», к.ф.-м.н. Мирсаитов Р.Г.
© Альметьевский государственный нефтяной институт, 2009 Содержание. Введение ………………………………………………………………………………41. Исходные данные, основные требования и этапы проектирования….………..4 2. Типы кулачковых механизмов…………..……………………………………….5 3. Циклограмма работы кулачкового механизма………………..………………...7 4. Угол давления и угол передачи движения………………………………………8 5. Графическое интегрирование………………….………………………………..10 6. Рекомендуемые масштабы величин…………………........................................13 7. Зависимость между масштабами линейных и угловых путей, скоростей и ускорений толкателя при графическом интегрировании….…………………..15 8. Симметричные и несимметричные диаграммы толкателя……………………17 9. Динамический синтез кулачковых механизмов типа I………………………..19 10. Динамический синтез кулачковых механизмов типа II……………………...21 11. Динамический синтез кулачковых механизмов типа III…………………….23 12. Метод обращения движения (инверсии)………………………………….….27 13. Кинематический синтез кулачковых механизмов типа I……………………27 14. Кинематический синтез кулачковых механизмов типа II…………………..32 15. Кинематический синтез кулачковых механизмов типа III………………….34 16. Вопросы для самоконтроля……………………………………………………35 Литература ………………………………………………………………………...36 Введение Кулачковые механизмы – плоские или пространственные механизмы с одной высшей кинематической парой, выполняющие самые разные функции, получили широкое распространение в механизмах перемещения рабочих органов различных машин-автоматов, в устройствах подачи станков, механизмов газораспределения двигателей внутреннего сгорания и во многих других случаях, когда требуется - вращательное или возвратно-поступательное движение ведомого звена по заданному закону. Воспроизведение движения ведомого звена кулачковые механизмы осуществляют теоретически точно. Кулачковый механизм, в большинстве случаев, является составной частью проектируемой машины. Он может использоваться как основной, но чаще является вспомогательным механизмом для выполнения технологической операции, последовательность и продолжительность которой согласуется с движением основного механизма. Проектирование кулачкового механизма заключается в определении взаимного расположения ведущего и ведомого звеньев и координат профиля кулачка, обеспечивающих заданный закон движения ведомого звена. При этом должны быть удовлетворены требования, определяющиеся технологическим процессом и эксплуатационными показателями механизма. Дополнительное условие синтеза – обеспечение допустимых углов давления во всех положениях механизма, то есть обеспечение отсутствия заклинивания кулачкового механизма.
1. Исходные данные, основные требования и этапы проектирования В заданиях на курсовой проект содержатся следующие исходные данные: 1. Структурная схема кулачкового механизма, показывающая характер взаимосвязей звеньев и их относительное расположение, тип кулачка, вид толкателя и характер его движения. 2. Максимальное перемещение толкателя – ход толкателя Smax или максимальный угол поворота толкателя βmax. 3. Фазовые углы: угол рабочего профиля кулачка и его составляющие в соответствии с циклограммой механизма. 4. Закон движения толкателя в виде графика изменения аналога ускорения ведомого звена в зависимости от угла поворота кулачка. 5. Допустимый угол давления 6. Направление вращения кулачка и частота его вращения. При проектировании кулачковых механизмов необходимо соблюдать следующие основные требования: · проектируемый механизм должен обеспечивать заданный закон движения; · механизм должен иметь наименьшие габариты при достаточной надежности работы. Проектирование кулачкового механизма делится на три основных этапа: 1. Определение кинематических передаточных функций, характеризующих изменение ускорения, скорости и перемещения толкателя в функции времени или угла поворота кулачка. 2. Определение основных размеров кулачкового механизма – минимального радиуса кулачка r0, эксцентриситета е или межосевого расстояния d. 3. Определение координат профиля (профилирование) кулачка.
Типы кулачковых механизмов
Плоские трехзвенные кулачковые механизмы состоят из стойки и двух подвижных звеньев, причем подвижные звенья образуют с ней низшие кинематические пары (вращательные или поступательные), а друг с другом — высшую кинематическую пару. Ведущее звено в кулачковом механизме называют кулачком, ведомое — толкателем. Элемент высшей кинематической пары, принадлежащий кулачку, называют профилем кулачка, а элемент, принадлежащий толкателю, называют профилем толкателя. Рассмотрим типы кулачковых механизмов, представленных в заданиях на курсовое проектирование.
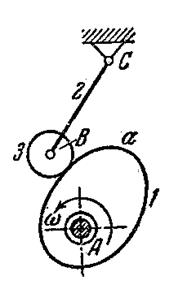
а б в Рис. 1
Кулачковый механизм типа I (рис.1, а) состоит из кулачка 1, толкателя 2 иролика 3. Кулачок, действуя на ролик, свободно вращающийся вокруг оси, заставляет толкатель двигаться поступательно в направляющих С-С. Если центр вращения кулачка лежит на продолжении прямолинейной траектории точки В толкателя, то кулачковый механизм называют центральным. Если же центр вращения не лежит на этой прямой, то кулачковый механизм называют внецентренным. Расстояние е от центра вращения кулачка до траектории точки В толкателя называют эксцентриситетом. Кулачковый механизм типа II (рис. 1, б) называется коромысловым. Кулачок 1 вращается с заданной угловой скоростью Кулачковый механизм типа III (рис. 1, в) состоит из кулачка 1 и плоского (тарельчатого) толкателя 2. Толкатель совершает прямолинейное возвратно-поступательное движение и касается кулачка во время движения различными точками своего прямолинейного профиля аа. Рис. 2 Большинство кулачковых механизмов относится к цикловым механизмам с периодом цикла равным 2p. В цикле движения толкателя в общем случае можно выделить четыре фазы (рис. 2): удаления из самого близкого (по отношению к центру вращения кулачка) в самое дальнее положение, дальнего стояния (или выстоя в самом дальнем положении), возвращения из самого дальнего положения в самое близкое и ближнего стояния (выстоя в самом ближнем положении). В соответствии с этим, углы поворота кулачка или фазовые углы делятся на:
Сумму φу + φд + φв называют рабочим углом и обозначают φр. Следовательно, φу + φд + φв = φр. Рис. 3 Графическое интегрирование При проектировании кулачковых механизмов закон движения толкателя обычно задается в виде функциональной зависимости аналога ускорения толкателя от угла поворота кулачка: При ω1 = const имеют место такие соотношения:
если толкатель перемещается прямолинейно (рис. 3, а); если же толкатель колеблется вокруг неподвижной оси (рис. 3, б), то
Для построения профиля кулачка достаточно иметь зависимости S = S (t) или ψ = ψ (t). Поэтому в указанных случаях приходится дважды интегрировать заданные зависимости. На рис. 4представлена кривая у" = у" (x), выражающая, в зависимости от типа кулачкового механизма, либо
Рис. 4 Площади F1 и F2, а также F’2 и F’1 должны быть равны между собой, поскольку скорость толкателя в начале и конце углов удаления и возвращения равна нулю. Проинтегрируем дважды графически заданную зависимость. Для этого: 1) построим ординаты ab, cd,..., соответствующие серединам интервалов 01, 12,..., и отложим отрезки Ob'= ab, Od' = cd на оси ординат; 2) соединим произвольно взятую точку Р 1 на продолжении оси х с точками b', d',...; 3) на рис. 4, б из точки О 1 проводим отрезок О1b" в интервале О11 параллельно лучу Р1b', отрезок b"d" в интервале 1—2 параллельно лучу P1d' и т.д. Полученная ломаная линия (в пределе — кривая) в графической форме представляет собой первый интеграл заданной зависимости, т. е. кривую у' — у' (х) и, значит, с учетом масштабов, либо Аналогично, интегрируя кривую у' = у' (х), получаем вторую интегральную кривую у = у (х), с учетом масштабов S=S(φ) (рис. 4, в), либо ψ = ψ(φ). Для определения произвольных постоянных интегрирования приходится задаваться некоторыми начальными условиями. В дальнейшем будем полагать, что в нижнем положении толкателя его скорость (линейная либо угловая) должна равняться нулю. Естественно также начало отсчета времени t относить к этому моменту. Таким образом, получаем следующие начальные условия для кулачковых механизмов: а) с поступательно движущимся толкателем t0 = 0; V0= 0; S0 = 0; б) с вращающимся толкателем t0 = 0; ωT=0; ψ0 = ψmin. Толкателя. На рис. 4, а кривая на участке φу - φд - φв имеет ось симметрии ММ,параллельную оси ординат и делящую, следовательно, этот отрезок абсциссы пополам. При таком задании, очевидно, должны иметь место следующие условия: площади F1 = F1’ и F2 = F2’. Вместе с тем, по абсолютной величине должны равняться между собой площади: F1 = |F2 |; |F2’| = F1’,так как по условиям работы скорость толкателя как в начале и конце подъема, так в начале и в конце опускания должны равняться нулю. По аналогичным соображениям имеет место и равенство: F3 = |F4|,так каквеличина подъема толкателя должна быть равна величине его опускания за время одного периода. Из этого следует, что в симметричных диаграммах угол φу поворота кулачка, соответствующий полному подъему толкателя, должен быть равен углу φв поворота кулачка, соответствующему возвращению толкателя из верхнего (дальнего) положения в нижнее (ближнее): φу = φв. Однако очень часто приходится проектировать кулачковые механизмы, в которых φу ≠ φв. Это имеет место в тех случаях, когда подъем толкателя, например, соответствует рабочему ходу, а опускание — холостому (или наоборот). Естественно, что на холостой ход желательно тратить меньше времени, и, следовательно, соответствующий ему угол поворота кулачка следует брать как можно меньше. Несимметричные диаграммы приходится строить в двойном масштабе, так как площади F1 ≠ F1’ и F2 ≠ F2’. Само собой разумеется, что применение двойных масштабов к кинематическим диаграммам является неудобным и трудоемким. Существует способ, позволяющий построить всю диаграмму в одном масштабе в случае, когда φу ≠ φв и получить, следовательно, на следующей диаграмме F3 = — F4,а значит, и у1 = у2. Таким образом, можно избежать неудобства применения двух масштабов. Этот способ справедлив, однако, лишь в тех случаях, когда оба участка диаграммы (рис. 5)заданы одноименными кривыми. Способ состоит в том, что наибольшие ординаты h’ и h" обоих участков диаграммы
Рис. 5 Рис. 6 В курсе теории механизмов и машин доказывается, что острый угол СЕН (заштрихован) определяет на плоскости геометрическое место точек, каждую из которых можно принять за центр вращения кулачка, причем при таком выборе угол γ передачи движения ни в одном положении механизма не будет меньше γmin. Соединив выбранный центр вращения кулачка с точкой А0, получим искомый минимальный радиус-вектор r0 кулачка. Если эксцентриситет не задан, то, чтобы получить кулачок с наименьшими размерами, следует центр вращения кулачка поместить в точке Е. Тогда r0 – ЕA0. Если задан эксцентриситет е, то на расстоянии е от прямой QR нужно провести прямую N0, параллельную QR, до пересечения в точке O со стороной СЕ угла СЕН. Отрезок 0А0 является минимальным радиусом r0 кулачка при данном эксцентриситете. Следует отметить, что чем ниже располагать центр вращения кулачка внутри угла СЕН, тем большим будет угол передачи движения, тем лучше будут условия работы механизма. Однако одновременно с улучшением условий работы будет увеличиваться радиус r0 и, следовательно, будут увеличиваться габариты механизма.
Рис. 7
Поместим центр вращения кулачка в точке О, находящейся внутри области RDN. Тогда отрезок ОА0 определяет минимальный радиус r0 кулачка, а отрезок ОС — расстояние d между центрами вращения толкателя и кулачка. Чем дальше от точки О внутри области RDN находится центр вращения кулачка, тем лучше становятся условия работы механизма, так как углы γ увеличиваются. Однако при этом размеры механизма также увеличиваются, так как возрастает минимальный радиус r0 кулачка и расстояние d. Рис. 8
2. Проводим касательную АВ к той части кривой, которая лежит во втором квадранте, под углом 45° к оси S. Несколько увеличенный отрезок ОВ с учетом масштаба является минимальным радиусом кулачка
Второй способ. Из неравенства (7) следует, что Отсюда вытекает такой способ определения: r min = S min. Наложим диаграммы (S — φ) и
На рис. 9 приводится уже просуммированная диаграмма при γ = 90°. Заметим, что rmin = Smin всегда больше нуля и поэтому приведенное выше неравенство показывает, что rmin должно быть больше наибольшей отрицательной ординаты, полученной при наложении диаграмм. Это обеспечивает существование приведенного неравенства во всех положениях механизма. Обозначим наибольшее абсолютное значение отрицательной ординаты через a. Тогда, гарантируя «запас», берем с некоторым увеличением найденное значение, а именно: rmin = Smin = (a + δ) μS,
где δ определяется из равенства δμS ≈ 10 мм.
Рис. 9
Рис. 10
Для построения ряда последовательных положений точки А толкателя в обращенном движении поступаем следующим образом: 1. Строим окружность радиуса ОВ0; 2. Откладываем от прямой ОВ0 в направлении, противоположном вращению кулачка, заданные фазовые углы φу; φд; φв; φб и получаем точки В4; В5; В9 пересечения сторон этих углов с окружностью радиуса ОВ0 . 3. Дуги В0В4 и В5В9,соответствующие углам φу и φв, делим на части в
соответствии с делениями оси абсцисс диаграммы s2 — φ1 (точки В1; В3; В6; В7; В8). 4. Засекаем радиусы ОВ1 ; ОB2; и т. д. дугами окружностей радиусов 0А1; 0А2 и т. д. в точках А1’; А2’ и т. д. Соединяя плавной кривой точки А0; А1’; А2’ и т. д., получаем теоретический профиль кулачка. Участки теоретического профиля (дуги А4’А5’, А9’А0), соответствующие фазовым углам φд и φб, описывается дугами окружностей радиусов ОА4’ и ОА0. Для получения практического профиля кулачка нужно построить огибающую дуг радиуса r ролика, имеющих центры на теоретическом профиле. На участках KL и DC практический профиль описываются дугами радиусов (ОА4’ — r) и (ОА0 — r). Для устранения самопересечения профиля кулачка, а также из конструктивных соображений длина r радиуса ролика должна удовлетворять двум условиям: r < 0,8 ρmin и r < (0,4 - 0,5)r0. Здесь ρmin — минимальный радиус кривизны профиля кулачка. Б. Случай, когда е ≠ 0 (рис. 11). Предположим, что кулачок вращается противоположно вращению часовой стрелки. Все построения выполняем в масштабе μs2. Через произвольную точку А0, лежащую на продолжении оси абсцисс диаграммы s2 — φ1, проводим вертикаль A0F — траекторию точки А толкателя, — и размечаем ее в соответствии с диаграммой s — φ для чего через точки a1; а2 и т. д. проводим горизонтальные прямые до пересечения с прямой A0F в точках Ах; А.2 и т. д. Слева от прямой A0F на расстоянии эксцентриситета е проводим прямую ЕО и засекаем ее из точки A0 дугой радиуса А0О,равного (в масштабе μs) заданному радиусу r0 теоретического профиля кулачка. Точка О является центром вращения кулачка. При заданном вращении кулачка против часовой стрелки эксцентриситет откладывается влево от траектории точки А0, а при вращении кулачка по направлению вращения часовой стрелки — вправо.
Рис. 11
Из точки О опускаем перпендикуляр OD0 на прямую A0F. Обратим движение механизма. Тогда кулачок будет представляться нам неподвижным. Траектория абсолютного движения точки А толкателя (прямая D0B0) в ее обращенном движении все время будет касаться окружности радиуса е в точках D1; D2; D3 и т. д. Для построения последовательных положений (А1’; А2’ и т. д.) точки А толкателя в обращенном движении поступаем следующим образом: 1) строим окружность радиуса ОВ0; 2) откладываем от прямой ОВ0 в направлении, противоположном вращению кулачка, заданные фазовые углы φу; φд; φв; φб и получаем точки В4; В5; В9 пересечения сторон этих углов с окружностью радиуса ОВ0 ; 3) дуги B0B4 и В5В9,соответствующие углам φ у и φв, делим на части в
соответствии с делениями оси абсцисс диаграммы s — φ, (точки В1; В2; В3; В6; В7; В8); 4) проводим из точек В1; В2 и т. д. касательные к окружности радиуса е (B1D1; B2D2 и т. д.); 5) засекаем касательные дугами окружностей радиусов 0А1, ОА2 и т. д. в точках A1’;А2’ и т. д. Соединяя плавной кривой точки A0; A1’;А2’ и т. д. получаем теоретический профиль кулачка. Определение радиуса r ролика и построение практического профиля производим так же, как и в случае, когда е = 0. Рис. 12 Вопросы для самоконтроля. 1. Плоский кулачковый механизм области применения, основные достоинства и недостатки. 2. Этапы проектирования кулачкового механизма. 3. Циклограмма работы кулачкового механизма (фазовые углы). 4. Геометрические параметры кулачкового механизма. 5. Типовые законы движения толкателя, их достоинства и недостатки. 6. Основные требования, предъявляемые при проектировании кулачкового механизма. 7. Критерии работоспособности кулачкового механизма, угол давления и угол передачи движения в высшей кинематической паре. 8. Основные приемы графического интегрирования. 9. Динамический синтез плоского кулачкового механизма типа I - определение минимального радиуса кулачка, радиуса ролика и эксцентриситета. 10. Динамический синтез плоского кулачкового механизма типа II - определение минимального радиуса кулачка, радиуса ролика и межосевого расстояния. 11. Динамический синтез плоского кулачкового механизма типа III - определение минимального радиуса кулачка и радиуса тарелки. 12. Метод обращения движения. 13. Построение центрового (теоретического) и конструктивного (действительного) профилей кулачка механизма типа I при проектировании графическим методом. 14. Построение центрового (теоретического) и конструктивного (действительного) профилей кулачка механизма типа II при проектировании графическим методом. 15. Построение центрового (теоретического) и конструктивного (действительного) профилей кулачка механизма типа III при проектировании графическим методом.
Литература 1. Артоболевский И.И. Теория механизмов и машин. М.: Наука, 1975. 638 с. 2. Курсовое проектирование по теории механизмов и машин /Кореняко А.С. и др./ под ред. А.С. Кореняко. Изд. 5-е.: Киев:«Вища школа», 1970. 330 с. 3. Матвеев Ю.А., Матвеева Л.В. Теория механизмов и машин: Учебное пособие.- М.: Альфа-М: ИНФРА-М, 2009. 320 с. 4. Теория механизмов и машин: Учебник для втузов /К.В. Фролов, С.А. Попов, А.К. Мусатов и др. / Под ред. К.В. Фролова. Изд. 5-е М.: Высш.шл., 2005. 496 с.
О.А. Шипилова, Н.И. Миндиярова, Е.Ю. Москвина
Проектирование Кулачковых механизмов
учебно-методическое пособие по курсовому проектированию по дисциплине «Теория механизмов и машин» для студентов специальностей 151001 «Технология машиностроения», 130602 «Машины и оборудование нефтяных и газовых промыслов» очной, заочной и очно-заочной форм обучения
Альметьевск 2009 УДК 621.01 Ш 63
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.43.244 (0.013 с.) |

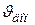 .
.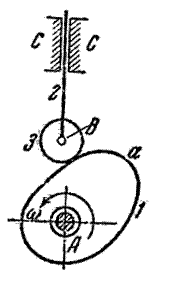
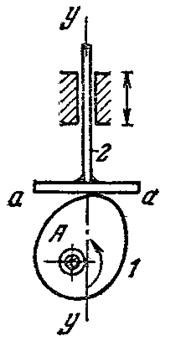
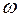 . Действуя на ролик 3, кулачок 1 заставляет коромысло 2 вращаться вокруг оси С. Расстояние ВС = l называют длиной коромысла. Буквой d обозначают расстояние АС между центрами вращения кулачка и толкателя.
. Действуя на ролик 3, кулачок 1 заставляет коромысло 2 вращаться вокруг оси С. Расстояние ВС = l называют длиной коромысла. Буквой d обозначают расстояние АС между центрами вращения кулачка и толкателя. - для механизмов с поступательно движущимся толкателем или
- для механизмов с поступательно движущимся толкателем или 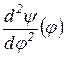 - для механизмов с вращающимся толкателем, так как для обеспечения режима технологического процесса к закону изменения скорости или ускорения толкателя часто предъявляются определенные требования.
- для механизмов с вращающимся толкателем, так как для обеспечения режима технологического процесса к закону изменения скорости или ускорения толкателя часто предъявляются определенные требования.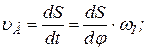 (1)
(1)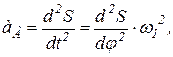 (2)
(2) (3)
(3)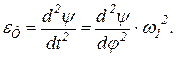 (4)
(4) либо
либо 


 либо
либо 
 берутся в отношении, обратно пропорциональном квадратам углов φу и φв, т. е.
берутся в отношении, обратно пропорциональном квадратам углов φу и φв, т. е. или
или  .
.
 .
.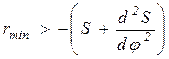
 (рис. 9) одну на другую и просуммируем их. Разумеется, для этого необходимо предварительно вычертить их в одном масштабе, т. е. нужно, чтобы
(рис. 9) одну на другую и просуммируем их. Разумеется, для этого необходимо предварительно вычертить их в одном масштабе, т. е. нужно, чтобы





