
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неоинституциональные модели потребительского выбора. Модель функционального спроса Ланкастера. Нефункциональный спрос: эффект присоединения к большинству, эффект сноба, эффект Веблена.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Неоинституциональные модели потребительского выбора. Модель функционального спроса Ланкастера. Нефункциональный спрос: эффект присоединения к большинству, эффект сноба, эффект Веблена. Функциональный спрос. Характеристики товаров и выбор потребителя (подход Ланкастера). Функциональным спросом является спрос на блага, который определяется исключительно потребительскими свойствами, присущими экономическому благу (товару или услуге).
Функциональный спрос зависит от максимизации функции полезности потребителя, он убывает или возрастает в зависимости от качеств этого блага с точки зрения потребителя, качеств, которые повышают полезность потребителя".
Ограниченность классической модели потребительского поведения заключается в том, что она базируется на субъективной информации. Предпочтения по отношению к различным товарам (даже если товары идентичны) субъективны; объективная информация ограничивается такими показателями, как цена и доход. Задача этого параграфа — исследовать проблему потребления на основе более объективных параметров. Новый подход к потребительской теории был впервые предложен Кельвином Ланкастером.
Подход Ланкастера основан на трех предпосылках
● всем благам присущи измеряемые характеристики, или атрибуты; ● атрибуты могут быть измерены объективными параметрами; ● полезность блага, основанная на атрибутах, объективно измерима.
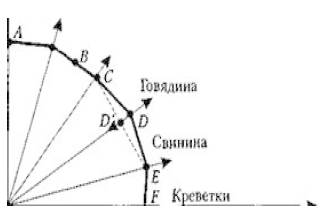
Например, два главных атрибута (характеристики), протеин (Z t) и жир (Z 2), содержатся в мясе и в его заменителях. Если бы это были единственные атрибуты, которые имеют существенное значение для потребителя, то функция полезности имела бы вид; U = U (Z,, Z 2). Функция полезности остается субъективной (разные люди имеют различные предпочтения относительно жира и протеина), но теперь к объективным характеристикам «цена» и «доход» добавляются не менее объективные «жир» и «протеин». На рисунке каждый вид продукта классифицирован по параметрам: «жир-протеин» в соответствии с удельным весом каждого из двух компонентов в товаре.
Относительные количества жира и протеина представлены с помощью наклонов «атрибутивных лучей», исходящих из осей координат. В данном случае пшеница и креветки являются двумя крайними случаями сочетаний протеина и жиров. Содержание жира увеличивается при переходе от пшеницы к рыбе, птице и т. п. Цены и доход определяют достижимую величину сочетаний жира и протеина и формируют границу характеристик: ABCDEF.
Граница характеристик (characteristic frontier): положение потребительского максимума продуктовых характеристик, которые определяются доходом потребителя, рыночными ценами и набором атрибутов, содержащихся в товарах.
Угол атрибутивного луча указывает удельный вес протеина и жира и объем данного блага, который может получить потребитель, если он потратит весь свой продуктовый бюджет на его покупку. К примеру, предположим, что 1 кг рыбы содержит 10 ед. протеина и 1 ед. жира. Если продуктовый бюджет потребителя составляет 100 р. в неделю, а цена рыбы 2,5 р. за килограмм, то потребитель может купить максимально 40 кг рыбы в неделю, что соответствует 400 ед. протеина и 40 ед. жира. Это определяет положение точки В на рисунке. Положение прочих точек (С, D, Е, F) определяется аналогично.
Функциональный и нефункциональный спрос. Функциональный спрос — спрос, обусловленный присущими данному благу потребительскими качествами.
Нефункциональный спрос — спрос, возникающий у потребителя не в силу потребительских характеристик товара, а под влиянием каких-либо других факторов.
Нефункциональный спрос в свою очередь делится на три неравные группы:
● Спрос, обусловленный внешними (экзогенными) воздействиями на полезность товара. Здесь выделяют:
○ эффект присоединения к большинству ○ эффект сноба ○ эффект показательного потребления
● Спекулятивный спрос ● Нерациональный спрос
Наиболее значительная часть нефункционального спроса обусловлена экзогенными воздействиями на полезность. Это означает, что полезность товара для потребителя увеличивается или уменьшается в зависимости от того, покупают ли этот товар другие люди, либо вследствие того, что этот товар имеет более высокую цену по сравнению с другими товарами.
Эффект сноба. Эффект сноба характеризуется величиной, на которую сократится индивидуальный спрос вследствие того, что другие тоже потребляют данный товар, т.е. вследствие увеличения рыночного спроса. Этот эффект выражает стремление людей к исключительности, стремление отличаться друг от друга, выделяться из толпы. Падение спроса тем больше, чем большим спросом данный товар пользуется у других покупателей.
И эффект присоединения к большинству и эффект сноба могут быть количественно оценены через коэффициент количественной эластичности, показывающий степень количественного изменения индивидуального спроса при изменении рыночного спроса на 1%. Коэффициент подсчитывается по формуле:
qi — величина индивидуального спроса на товар i; Qi — величина рыночного спроса на товар i;
Если Eq > 0, то имеет место эффект присоединения к большинству Если Eq < 0, то наблюдается эффект сноба.
Абсолютное значение данного коэффициента характеризует величину рассматриваемых эффектов.
Эффект Веблена. Эффект показательного потребления, или эффект Веблена отражает такое на первый взгляд парадоксальное явление, как увеличение спроса на некоторый товар в силу того, что он имеет более высокую по сравнению со своими аналогами цену.
Эффект Веблена характеризует величину, на которую возрастает индивидуальный спрос вследствие увеличения цены на рассматриваемый товар.
Эффект наблюдается в том случае, когда потребитель ассоциирует повышенную цену с большей престижностью, что и вызывает дополнительный спрос.
Обратная зависимость между ценой и величиной спроса сохраняется, но сама кривая спроса сдвигается под воздействием эффекта вправо, поскольку в глазах потребителя один и тот же товар с низкой ценой (P1 непрестижный) и с высокой ценой (P2 престижный) являются различными товарами с различными кривыми спроса соответственно d(P1) и d(P2).
Количественное значение эффекта Веблена может быть оценено через ценовую эластичность спроса, характеризующую степень изменения спроса при изменении цены на 1%.
Коэффициент ценовой эластичности спроса подсчитывается по уже известной нам формуле:
Q(P) — функция спроса по цене P — рыночная цена
Если эффект Веблена отсутствует, и товар не принадлежит к группе товаров Гиффена, то коэффициент ценовой эластичности является отрицательным, E<0.
Положительное значение коэффициента, E>0, может говорить о существовании эффекта показательного потребления тем более значимого, чем выше абсолютное значение данного коэффициента.
Выбор в условиях неопределенности. Санкт – Петербургский парадокс. Предпосылки концепции ожидаемой полезности. Теория Неймана-Моргенштерна. Кривые безразличия для функции ожидаемой полезности. Ожидаемая полезность по Нейману – Моргенштерну и тестирование этой гипотезы. Парадокс Алле. Рамочные эффекты. Денежные лотереи. Стохастическое доминирование. Достоверный эквивалент к риску. Мера Арроу – Пратта абс несклонности к риску. CARA. Обмен в условиях неопределенности. Индивидуальные и системные риски. Выбор между рискованными и безрисковыми активами. Парадокс Алле. Парадокс демонстрирует неприменимость теории максимизации ожидаемой полезности в реальных условиях риска и неопределённости. Автор корректно, с позиций математики, объясняет суть парадокса. Парадокс демонстрирует, что реальный агент, ведущий себя рационально, предпочитает не поведение получения максимальной ожидаемой полезности, а поведение достижения абсолютной надежности.
Сам Алле провёл психологический эксперимент, описанный ниже, и получил парадоксальные результаты.
Индивидам предлагают выбор по одному решению из двух пар рискованных решений.
В первом случае в ситуации A есть 100 % уверенность в получении выигрыша в 1 млн франков, а в ситуации B имеется 10 % вероятность выигрыша в 5 млн франков, 89 % — в 1 млн франков и 1 % — не выиграть ничего.
Во втором случае тем же индивидам предлагается сделать выбор между ситуацией C и D. В ситуации C имеется 10 % вероятности выигрыша в 5 млн франков и 90 % не выиграть ничего, а в ситуации D 11 % составляет вероятность выигрыша в 1 млн франков и 89 % — не выиграть ничего. Алле установил, что значительное большинство индивидов в этих условиях предпочтет выбор ситуации A в первой паре и ситуации C во второй. Этот результат воспринимался как парадоксальный. В рамках существовавшей гипотезы индивид, отдавший предпочтение выбору А в первой паре, должен выбрать ситуацию Д во второй паре, а остановивший выбор на В должен во второй паре отдать предпочтение выбору С. Алле математически точно объяснил этот парадокс. Его основной вывод гласил, что рационально действующий агент предпочитает абсолютную надежность.
Парадокс можно сформулировать в виде выбора между двумя вариантами, в каждом из которых с некоторой вероятностью достаётся та или иная сумма денег:
Здесь X — неизвестная выбирающему сумма.
Какой выбор будет более разумным? Результат останется прежним, если «неизвестная сумма» X — это 100 миллионов? Если это «ничего»?
Математическое ожидание в первом варианте равно
а во втором:
поэтому математически второй вариант B выгоднее независимо от значения X. Но люди боятся нулевого исхода в варианте B и поэтому чаще выбирают A. Однако если
Теоретические концепции поведения экономических агентов в условиях неопределенности и их тестирование. «Рамочные» эффекты. Принимая решение в условиях неопределенности, индивид всегда участвует в своего рода лотерее. Например, покупая некую акцию, инвестор может как получить значительный выигрыш, так и лишиться инвестированных средств Обозначив через xi исходы в такого рода лотерее, мы можем записать эту лотерею следующим образом L1 р о х1 что означает: "Индивид с вероятностью р получит приз х1 и с вероятностью (1 - р) - приз х2 " Альтернативой участию в этой лотерее может быть покупка иной акции L2 q о х3 Какую из этих двух лотерей предпочтет индивид? При совпадении перечня исходов(призов) в обеих лотереях (х1= х3; х2= х4 ) ответ на этот вопрос может быть обусловлен вероятностным распределением выигрышей. Изменив вероятности получения призов в сторону увеличения вероятности получения лучшего приза, мы получим новую лотерею, которая будет стохастически доминировать исходную (более подробно о стохастическом доминировании будет сказано позднее). Но это отнюдь не снимает проблему ранжирования лотерей при отсутствии четко выраженного стохастического доминирования, столь частого при большем количестве возможных исходов. Лотереи. Сведение сложных лотерей к простым. Простая лотерея может быть описана как вектор вероятностей выпадения возможных исходов: L(р)=(р1, р2,..., рn), где Геометрически простая лотерея соответствует точке на (n -1) -мерном симплексе D. Рис.1.1. n = 2
Рис.1.2. n = 3
Сложные лотерии (compound lotteries) - в отличие от простых лотерей - допускают возможность рассмотрения в качестве возможных исходов не только получение индивидом неких конкретных "призов", но так называемых "вторичных" лотерей. Сложной, например, является лотерея, включающая в перечень возможных призов билеты следующего тура этой лотереи. Математически сведение сложной лотереи к простой, т.е. определение вероятностей получения конечных призов, может быть осуществлено путем расчета сумм условных вероятностей, т.е. вероятностей получения этих призов во вторичных лотереях, взвешенных по вероятностям выпадения вторичных лотерей: p(xi) = Например, если призами в первичной лотерее выступают лотереи L1=(0.6, 0.4) и L2=(0.2, 0.8), причем вероятность выигрыша L1 равна 2/3, а вероятность выигрыша L2 равна соответственно 1/3, то такая сложная лотерея будет эквивалентна простой лотерее с вероятностями получения конечных призов (0.6 х (2/3) + 0.2 х (1/3), 0.4 х (2/3) + 0.8 х (1/3)) = (14/30, 16/30). Графически этот процесс сведения этой сложной лотереи к простой представлен на рис. 1.3.а, а следующий рисунок 1.3.б иллюстрирует сходную процедуру в предположении существования (в каждой из двух вторичных лотерей) уже не двух, а трех конечных призов.
Допустимость подобного сведения сложных лотерей к простым следует оговорить как отдельную предпосылку дальнейшего анализа (RCLA - the reduction of compound lotteries axiom), ибо с точки зрения отдельного индивида различные сложные лотереи, сводимые к одной и той же простой лотерее, могут оцениваться весьма различным образом. В частности, Джошуа Ронен (Ronen,1973) убедился, что даже простая перестановка двух этапов лотереи влияет на ее привлекательность для индивидов,а именно, семидесятипроцентный шанс получить 100 долл с вероятностью 30 % оказался более привлекательным для опрашиваемых, чем тридцатипроцентный шанс получить 100 долл с вероятностью 70 %. Но подобного рода соображения мы пока оставим в стороне, и в дальнейшем будем полагать эквивалентными различные сложные лотереи, сводимые к одной и той же простой лотерее.
Спрос на страхование. Как несклонность к риску влияет на поведение человека? Не склонный к риску человек интересуется не только ожидаемой величиной потерь, но и возможным размером потерь. Не склонный к риску человек сочтет ситуацию, которая чревата 10%-ным риском потери 20 тыс. долл. Более неблагоприятной, чем ситуация, чреватую 100%-ной вероятностью потери 2000 долл., хотя ожидаемая величина потерь во всех случаях одинаковая. Не склонные к риску стороны не любят неопределенности в отношении самой величины потерь.
Существует три способа, с помощью которых не склонный к риску человек может превратить неопределенный исход в определенный. Во-первых, он может купить рыночную страховку. Во-вторых, он может сам застраховать себя, например, отложив некоторую сумму денег, которая потребуется, чтобы покрыть потери. В-третьих, он может использовать возможности, предоставляемые договором, например, при покупке рискованных активов он может предложить за них более низкую цену.
Рассмотрим вариант с покупкой рыночной страховки. Покупка рыночной страховки
Владелец имеет автомобиль стоимостью 20000 долл. Вероятность угона автомобиля составляет 10%. В табл. 17 показано два возможных варианта благосостояния этого человека: со страховкой и без нее. Решение приобрести страховку не влияет на его ожидаемое благосостояние, оно по-прежнему составляет 18 тыс. долл.
Приобретение страховки не изменяет ожидаемого благосостояния, однако страховка способствует достижению более высокого уровня полезности для владельца автомобиля.
Владелец автомобиля — это сторона, не склонная к риску. Если риск несет не склонная к риску сторона, то это приведет к большему сокращению ожидаемой полезности дохода, чем несение риска менее склонной или нейтральной стороной. Поэтому та сторона, которая обнаруживает большую несклонность к риску, может заплатить менее несклонной или нейтральной к риску стороне за то, чтобы та приняла риск на себя, и обе стороны окажутся в более благоприятном положении, с точки зрения ожидаемой полезности. Владелец автомобиля будет готов заплатить 100 долл. за то, чтобы превратить неопределенное будущее в определенное, и его готовность платить говорит о том, что он не склонен к риску.
Страхование позволяет индивиду обменять риск больших потерь на определенность малых потерь.
Если имеются не склонные к риску стороны, то это означает, что распределение риска само по себе влияет на богатство общества. Предположим, что благосостояние общества — это сумма ожидаемых полезностей сторон. Перераспределение риска от не склонных к риску к нейтральным к риску сторонам приведет к повышению богатства общества.
Общественное благосостояние повышается не только когда риск полностью перекладывается с более несклонной к риску стороны на менее несклонную или нейтральную к риску сторону, но и когда риски делятся между не склонными к риску сторонами.
3. Теория игр. Дилемма заключенных. Равновесие в доминирующих стратегиях. Равновесие по Нэшу. Последовательные игры с совершенной информацией. Метод обратной индукции и common knowledge. Соображения, связанные с правомерностью применения метода обратной индукции. Простейшая модель торга (дележка доллара). Информационное множество. Усечение игры. Совершенное равновесие по Нэшу. Повторяемые игры. Сигнализирующие игры. Примеры взаимодействий, описываемых этой игрой. В первоначальной версии игры рассматривалась ситуация, в которой двоих заключенных — соучастников преступления — допрашивают в отдельных комнатах. У каждого из заключенных имеется выбор: либо признаться в преступлении и тем самым впутать другого, либо отрицать свое участие в преступлении. Если признается лишь один из заключенных, его освободят, и обвинение падет на другого заключенного, которого приговорят к 6 месяцам тюремного заключения. Если оба заключенных будут отрицать свою причастность к преступлению, обоих продержат в тюрьме по 1 месяцу в связи с соблюдением формальностей, а если оба игрока признаются, обоих приговорят к 3 месяцам тюремного заключения. Платежная матрица для этой игры приведена в таблице. Записи в каждой клетке матрицы представляют полезность, приписываемую каждым из игроков различным срокам пребывания в тюрьме, которую мы для простоты будем считать продолжительностью их тюремного заключения, взятой со знаком "минус".
Поставьте себя на место игрока A. Если игрок B решит отрицать, что совершил преступление, то, конечно, вам лучше признаться, так как тогда вас освободят. Подобным же образом если игрок B признается, то вам лучше признаться, так как в этом случае вас приговорят не к 6 месяцам тюремного заключения, а только к 3. Следовательно, что бы ни делал игрок B, игроку A выгоднее признаться.
То же самое можно сказать и об игроке B — ему тоже выгоднее признаться. Следовательно, единственное равновесие по Нэшу в этой игре — исход, при котором оба игрока признаются. В действительности исход, при котором оба игрока признаются, — это не только равновесие по Нэшу, но и равновесие при доминирующих стратегиях, поскольку у каждого игрока имеется один и тот же оптимальный выбор, независимый от выбора другого игрока.
Но если бы они оба держали язык за зубами, им обоим это было бы выгоднее! Если бы они оба могли быть уверены в том, что другой промолчит, и договорились бы между собой не признаваться, то выигрыш каждого составил бы —1, что было бы выгодно обоим. Стратегия ("отрицать", "отрицать") эффективна по Парето, другой стратегии, которая была бы выгодна сразу обоим, нет, в то время, как стратегия ("признаться", "признаться") неэффективна по Парето.
Проблема состоит в том, что заключенные лишены возможности координировать свои действия.
Если бы каждый из них мог доверять другому, благосостояние обоих повысилось бы.
Дилемма заключенного применима к широкому кругу экономических и политических явлений.
Рассмотрим, например, проблему контроля над вооружением. Можно интерпретировать стратегию "признаться" как "развертывать новые ракеты", а стратегию "отрицать" — как "не развертывать новые ракеты". Обратите внимание на то, что выигрыши вполне подходят для такой игры. Если мой противник развертывает свои ракеты, я, конечно, захочу развертывать свои несмотря на то, что наилучшей стратегией для нас обоих было бы придти к соглашению о неразвертывании ракет. Однако если не существует способа заключить соглашение, реально обязывающее его участников к выполнению, мы в итоге оба развернем ракеты и благосостояние обоих понизится.
Другой хороший пример применения дилеммы заключенного — проблема мошенничества в картеле. Теперь можно интерпретировать "признаться" как "превысить квоту выпуска", а "отрицать" — как "придерживаться первоначальной квоты". Если вы думаете, что другая фирма собирается придерживаться своей квоты, вам выгоднее превысить свою квоту. А если вы думаете, что другая фирма превысит свою квоту выпуска, то и вы тоже можете это сделать!
Дилемма заключенного вызвала большие споры в отношении того, как же "правильно", или, точнее, как разумнее играть в эту игру. Ответ, похоже, зависит от того, разыгрывается ли игра в течение одного периода или повторяется бесконечное число раз.
Если в игру играют только один раз, то разумной представляется стратегия нарушения условий соглашения — в рассматриваемом примере это стратегия "признаться". В конце концов, что бы ни делал другой, вам выгоднее следовать данной стратегии, и у вас нет способа повлиять на поведение другого игрока.
Равновесие по Нэшу. Пара стратегий приводит к равновесию по Нэшу, если выбор, сделанный A, оптимален при данном выборе B, а выбор, сделанный B, оптимален при данном выборе A.
Помните, что ни один из игроков не знает, что будет делать другой, когда ему самому придется выбирать стратегию. Однако у каждого игрока могут иметься какие-то ожидания в отношении возможного выбора другого игрока. Равновесие по Нэшу можно истолковывать как пару таких ожиданий в отношении выбора каждого игрока, что когда выбор каждого становится известным, ни один из игроков не хочет изменить свое поведение.
В случае, представленном в таблице, стратегия ("верх", "слева") приводит к равновесию по Нэшу. Чтобы это доказать, обратите внимание на то, что если A выбирает "верх", то в лучше всего выбрать "слева", таккак выигрыш от выбора "слева" составляет для B 1, а от выбора "справа" — 0. Если же B выбирает "слева", то для A лучше всего выбрать "верх", поскольку тогда A получит выигрыш 2, а не 0.
Таким образом, если A выбирает "верх", то оптимальным для B будет выбор "слева"; а если B выбирает "слева", то оптимальным для A будет выбор "верх". В итоге мы имеем равновесие по Нэшу: выбор каждого игрока оптимален при данном выборе другого игрока.
Понятию равновесия по Нэшу нельзя отказать в определенной логике. К сожалению, с ним связаны и некоторые проблемы. Во-первых, игра может иметь больше одного равновесия по Нэшу. В самом деле, в таблице выбор ("низ", "справа") также есть равновесие по Нэшу. Вы можете либо проверить это с помощью аргументации, использованной выше, либо просто обратить внимание на то, что структура игры симметрична: B имеет при одном исходе те же выигрыши, что A при другом, так что, доказав, что ("верх", "слева") есть равновесие, мы тем самым доказали и что ("низ", "справа") тоже равновесие.
Вторая проблема, связанная с понятием равновесия по Нэшу, состоит в том, что существуют игры, вообще не имеющие равновесия по Нэшу в том смысле, о котором шла речь. Рассмотрим, например, случай, описанный в таблице. Здесь равновесия Нэша в том виде, в каком оно изучалось нами, не существует. Если игрок A следует стратегии "верх", то игрок B захочет выбрать стратегию "слева". Но если игрок B следует стратегии "слева", то игрок A хочет следовать стратегии "низ". Аналогично если игрок A следует стратегии "низ", то игрок B будет следовать стратегии "слева". Если игрок В выбирает стратегию "справа", то А выбирает стратегию "верх".
Равновесия с доминирующими стратегиями хороши, но встречаются не так уж часто. Например, в игре, описанной в таблице, нет равновесия с доминирующими стратегиями. В ней при выборе игроком B стратегии "слева" выигрыш для A составляет 2 или 0. Если В выбирает "справа", то выигрыш А — от 0 до 1. Это означает, что когда B выбирает стратегию "слева", A захочет выбрать стратегию "верх"; а когда B выбирает стратегию "справа", A захочет выбрать стратегию "низ".
Следовательно, оптимальный выбор A зависит от того, каких действий он ожидает от B.
Однако, возможно, равновесие с доминирующими стратегиями связано с чересчур большими требованиями. Вместо требования, чтобы выбор, сделанный игроком A, был оптимальным для всех выборов игрока B, можно просто потребовать, чтобы он был оптимальным для всех оптимальных выборов, сделанных B. Ведь если B — хорошо информированный умный игрок, он захочет выбирать только оптимальные стратегии. (Хотя то, что оптимально для B, будет зависеть также от выбора, сделанного A!).
Основополагающие принципы анализа контрактных обязательств. Асимметрия информации как причина оппортунистического поведения агентов. Асимметричная информация и неблагоприятный отбор на рынке потребительских товаров и услуг. Рынок «лимонов»: модель Акерлофа. Неблагоприятный отбор - одна из моделей оппортунистического поведения, предшествующего заключению контракта. Возможность неблагоприятного отбора обусловлена асимметрией информации:
● покупатели в момент покупки (а иногда и позже) не в состоянии оценить качество приобретаемых им товаров или услуг; ● страховые компании не в состоянии оценить вероятность наступления страхового случая у лица (или фирмы), обратившегося за страховкой; ● банки не в состоянии оценить вероятность невозврата кредитов заемщиками; ● наймодатель не может оценить "качество" нанимаемых работников; ● регулирующий орган не обладает достаточной информацией о уровне издержек регулируемых фирм; ● владелец патента не в полной мере может оценить выигрыш возможных покупателей патента от его использования.
Впервые внимание на трудности, возникающие на рынке в связи с асимметрией информации на стадии до заключения сделки, обратил внимание Акерлоф в 1970 году. Он рассмотрел механизм неблагоприятного отбора на примере рынка подержанных автомобилей.
На этом рынке продаются хорошие автомобили, которые на жаргоне называются «сливы», и плохие автомобили (на жаргоне — «лимоны»).
Продавцы располагают большей информацией о качестве автомобилей, которые они продают, чем покупатели. Но поскольку покупатели не могут провести различие между сливами и лимонами, то и хорошие, и плохие автомобили продаются по одной цене. Акерлоф утверждает, что в этой ситуации на рынке останутся в основном лимоны, и, возможно, хорошие автомобили вообще не будут предлагаться к продаже.
Проиллюстрировать проблему неблагоприятного отбора можно с помощью простого числового примера. Пусть 100 человек, желают продать свои подержанные автомобили, а 100 человек, желают купить подержанные автомобили. Всем известно, что 50 автомобилей — это автомобили хорошего качества (на жаргоне — «слива»), а 50 автомобилей — это автомобили плохого качества (на жаргоне — «лимоны»). Владелец «лимона» готов продать свой автомобиль за 2000 долл., а владелец «сливы» готов продать автомобиль за 4000 долл. Покупатели готовы платить 2400 долл. за «лимон» и 4800 долл. за «сливу». Проблем не возникало бы, если бы проверить качество «лимонов» было легко. «Лимоны» продавались бы по цене от 2000 до 2400 долл., а «сливы» — по цене от 4000 до 4800 долл. Однако, покупатели не располагают информацией о качестве отдельных автомобилей. Автомобиль с равной вероятностью может оказаться и «сливой», и «лимоном». Типичный покупатель готов оплатить ожидаемую стоимость автомобиля: 1/2 · 2400+ 1/2 · 4800 = 3600 долл.
Кто захочет продать свой автомобиль по этой цене? Владельцы «лимонов» готовы это сделать, но владельцы «слив» хотят продать свой автомобиль по цене не меньше 4000 долл. Цена, которую должны заплатить за «средний» автомобиль покупатели, меньше той цены, по которой готовы продать свой автомобиль продавцы «слив». По цене 3600 долл. к продаже будут предложены только лимоны. Но если бы покупатель был уверен, что ему достанется «лимон», он не захотел бы заплатить за нее 3600 долл. На самом деле равновесная цена установилась бы где-то между 2000 и 2400 долл. По этой цене предлагались бы к продаже только «лимоны», и поэтому покупатели справедливо ожидали бы, что им достанется «лимон». Сливы на этом рынке вообще не предлагаются к продаже. Итак, несмотря на то, что цена, по которой покупатели готовы купить «сливы», превышает цену, по которой продавцы готовы их продать, ни одна из этих сделок не состоится.
Методы противодействия неблагоприятному отбору на рынке потребительских товаров
● Фирмы: предоставление гарантии на продаваемый товар или предоставляемую услугу, репутация, стандарты и сертификаты качества. ● Государство: защита потребителей и защита от недобросовестной конкуренции (высокие трансакц. издержки). Методы противодействия неблагоприятному отбору на рынке страховых услуг ● Перечень нестраховых случаев. Например оговаривается, что выплата страховки на случай самоубийства осуществляется страховой компанией только в том случае, если оно произошло не ранее, чем через 1- 2 года после заключения договора. Тем не менее, статистика свидетельствует, что эта мера не слишком эффективна: пик самоубийств приходится на 13 и 25 месяцы с момента заключения страхового договора. ● Страхование по месту работы (что усредняет вероятность наступления некоторых страховых случаев, или позволяет оценить риск более точно ввиду однородности страхуемой группы). Государственное страхование простейшая версия: государство преодолевает "провалы рынка".
Методы противодействия неблагоприятному отбору на рынке банковских кредитов: рационирование кредитов.
Способ борьбы - не увеличивать процентную ставку, если существует избыточный спрос, а рационировать кредиты(нормировать их).
В принципе выделяют два типа противодействия неблагоприятному отбору, различающихся в зависимости от того, какая из сторон (информированная или неинформированная) его осуществляет: сканирование и сигналы.
5. Методы противодействия неблагоприятному отбору: сканирующие контракты. Информационная рента. Контракты первого и второго наилучшего. Игровое представление сканирующих взаимодействий. Дискриминация по количеству (дискриминация второго рода). Дискриминация по качеству. Сканирование на рынке страхования. Сканирующие контракты. Сканирование (screening): противодействие вырождению рынка неинформированной, т.е. страдающей от асимметрии информации, стороны, которая делает первый ход, предлагая контракт (первый ход - за неинформированной стороной).
Рассмотрим просеивание на примере заработной платы, возрастающей в зависимости от стажа работы. Эмпирические исследования обнаруживают связь между заработной платой и стажем работы: с увеличением стажа и опыта работы возрастает оплата труда. Джоан и Стивен Сэлоп рассматривают подобную схему оплаты труда как метод просеивания с целью сокращения текучести работников. Уход работников сопряжен с потерями для всех фирм, но особенно большие потери возникают, когда фирма, к примеру, вкладывает значительные средства в подготовку работников. Поэтому фирмы бывают заинтересованы в привлечении работников, которые менее склонны к перемене места работы.
Решение, использующее стратегию просеивания, заключается в том, чтобы предложить такой контракт о занятости, который привлек бы только нужный тип работника. Фирма предлагает относительно низкую первоначальную оплату труда, а затем, после того как работник проработал на фирме значительный период времени, его вознаграждение становится выше, чем рыночная ставка оплаты труда. Возрастающая с увеличением стажа и опыта работы заработная плата «просеивает» все множество потенциальных работников, потому что эта схема оплаты труда более привлекательна для работников, которые имеют намерение оставаться на этой фирме, и совсем не нравится работникам, которые не намерены длительное время работать на данной фирме, потому что из-за преждевременного увольнения они недополучат доход, возрастающий пропорционально увеличению стажа их работы в данной организации.
Неоинституциональные модели потребительского выбора. Модель функционального спроса Ланкастера. Нефункциональный спрос: эффект присоединения к большинству, эффект сноба, эффект Веблена.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.056 с.) |


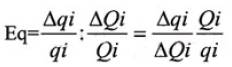



 ,
, ,
, , то психологический барьер устраняется, и большинство уходит от варианта A.
, то психологический барьер устраняется, и большинство уходит от варианта A. (1 - р) о х2,
(1 - р) о х2, ip i=1 и p i ≥ 0 для всех i =1,..., n.
ip i=1 и p i ≥ 0 для всех i =1,..., n.


 Lj) p(Lj).
Lj) p(Lj).









