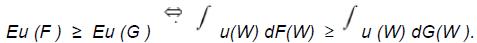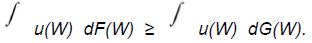Стохастическое доминирование.

Стохастическое доминирование 1-ого рода:

Если распределение F первично стохастически доминирует распределение G, то при распределении выигрышей F мат. ожидание выигрыша будет больше, чем при распределении G и ожидаемая полезность будет больше(Eu(F) > Eu(G))

 

Стохастическое доминирование 2-ого рода:

Распределение F вторично стохастически доминирует распределение G, если при одинаковом мат. ожидании дисперсия выигрышей G больше.

 

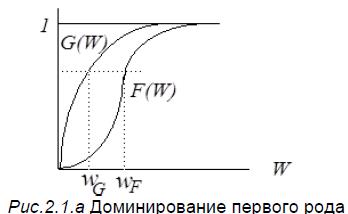
Стохастическое доминирование первого рода.

Рассмотрим два распределения F(W) и G(W)(см. рис(2.1.а).

С одной стороны, с некоей заданной вероятностью можно получить выигрыш

W ≤ wF - при распределении F и W ≤ wG - при распределении G. Т.к. F(W) ≤ G(W) для любого W, то, следовательно, wF > wG, что позволяет оценивать распределение F как менее рискованное. Иначе, более корректно, эту мысль можно сформулировать, указав на стохастическое доминирование распределения F распределения G.

 

Def. Распределение F(W) первично стохастически доминирует распределение G(W) (F(W) first-order stochastically dominates G(W)), тогда и только тогда, когда F(W) ≤ G(W) для любого W.

Соответственно, если распределение F первично стохастически доминирует

распределение G, то

 

• при распределении выигрышей F математическое ожидание выигрыша

будет выше чем при распределении G:

Графически это может интерпретироваться следующим образом(простоты ради зададим в данном случае совпадающие интервалы выигрышей):

• при распределении выигрышей F ожидаемая полезность будет выше, чем при распределении G, т.е. для любой неубывающей функции u(W) выполняется условие

Несмотря на то, что стохастическое доминирование первого рода позволяет нам проранжировать лотереи как по уровню математического ожидания выигрыша, так и по уровню их ожидаемой полезности, обратное неверно, т.е. ни по уровню математического ожидания выигрыша, ни по уровню ожидаемой полезности нельзя делать вывод о стохастическом доминировании первого рода, поскольку ранжирование лотерей с точки зрения доминирования первого рода является частичным. Например, распределение G(W) первично стохастически доминируется распределениями F(W) и F '(W), но не существует возможности,

рассматривая лишь доминирование первого рода, проранжировать эти два последние распределения.

Несколько упрощая рассмотрение стохастического доминирования второго рода, сконцентрируемся лишь на тех распределениях, которые характеризуются совпадением математических ожиданий выигрышей.

 

Итак, две игры могут иметь одно и тоже математическое ожидание выигрыша, но различаться в степени своей рискованности. Например, игра, в которой с вероятностью 1/2 можно выиграть и с вероятностью 1/2 проиграть h долларов всегда будет менее рискованной чем игра, где с равными вероятностями можно выиграть или проиграть 2 h долларов. В подобном случае уместно говорить о стохастическом доминировании второго

рода или вторичном стохастическом доминировании.

 

Def. Распределение F(W) вторично стохастически доминирует

распределение G(W) (F(W) second-order stochastically dominates G (W)),

имеющее такое же математическое ожидание

если распределение G предполагает больший разброс выигрышей, т.е. его

дисперсия больше.

 

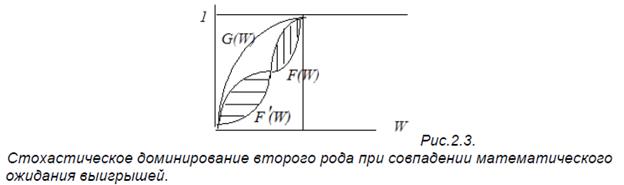
Пример. Сравним две игры, имеющие распределение G(W) и F(W). В первой игре с вероятностями 0.25 можно выиграть 1, 2, 3 и 4. Во второй с вероятностями 0.5 можно получить 2 и 3. В обоих случаях математическое ожидание одинаково - 2.5, что графически иллюстрируется совпадением площадей заштрихованных фигур.

 

Но поскольку в распределении G(W) задан больший разброс выигрышей, т.е. его дисперсия выше, чем при распределении F(W), оно является более рискованным.

Без доказательства приведем теорему, гласящую, что, если распределение F(W) вторично стохастически доминирует распределение G(W), то для любой возрастающей вогнутой функции полезности u(W) выполняется условие

 

Достоверный эквивалент лотереи, рисковая премия, рисковая