
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор в условиях неопределенности.Содержание книги
Поиск на нашем сайте
Факторы, обусловливающие необходимость учета фактора неопределенности многообразны.
● Характеристики некоторых товаров, приобретаемых потребителем, изначально не могут быть точно определены в момент покупки. Например, это касается рискованности и доходности ценных бумаг, выпускаемых компаниями. ● К неопределенности приводит действие внешних факторов (states of the World, state of Nature) влияющих на выбор, осуществляемый индивидом, но никак от него не зависящих. Например, это может касаться регулятивных, правовых, коньюнктурных и пр. изменений, непосредственно затрагивающих деятельность компании и интересы акционеров. ● Неопределенность может порождаться непредсказуемым поведением контрагентов, например, благосостояние инвесторов в существенной степени зависит от того, насколько эффективным будет руководство компанией, осуществляемое менеджерами, от того окажется политика, проводимая Советом директоров компании и в какой в какой степени, она сможет препятствовать возможным злоупотреблениям со стороны высших менеджеров и пр.
Санкт – Петербургский парадокс. Собственно привлекательность лотереи или игры можно попытаться оценить, определив уровень ее среднего выигрыша Е(W) = Однако еще в 18 веке такого рода подход начал вызывать серьезные возражения. В частности, Николас Бернулли в 1728 году обратил внимание на то, что ни один игрок не будет готов заплатить сколь-нибудь заметную сумму за участие в игре, математическое ожидание выигрыша в которой равно бесконечности. Суть рассмотренной им игры состояла в следующем: бросается монета, и в том случае, если орел выпадает в i - ом бросании, игрок получает выигрыш, равный 2^i. Вероятность выпадения орла в i - ом бросании составляет рi = (1/2)i, т.е. 1/2, 1/4 и т.д.
Е(W) = Парадоксальность этой ситуации состоит в том, что не найдется желающих платить, скажем 1 млн долл, за право участия в подобной игре, несмотря на то, что эта сумма несопоставимо меньше математического ожидания выигрыша - бесконечности.
Собственно, одновременно выдвинутая Габриэлем Крамером и Даниэлем Бернулли гипотеза о том, что важна не сама сумма выигрыша, а та полезность которую получает потребитель1, не является решением этого так называемого Санкт-Петербургского парадокса, но она способствовала весьма здравому теоретическому переосмыслению проблемы.
Привычные аксиомы потребительского выбора, лишь несколько модифицированные применительно к рассматриваемым ситуациям неопределенности.
Мы будем полагать, что предпочтения индивида на пространстве простых лотерей L асимметричны и негативно транзитивны. Во многом мы повторим традиционные аксиомы анализа поведения потребителя, когда будем говорить о том, что
- объекты выбора (в данном случае лотереи) должны быть четко определены; -ситуации с одними и теми же исходами должны вести к одинаковым решениям; - индивид должен быть в состоянии произвести анализ имеющихся альтернатив; -предпочтения относительно лотерей должны быть транзитивны, локально ненасыщаемы и т.д.
Особое положение в перечне исходных аксиом занимает аксиома непрерывности предпочтений индивида относительно простых лотерей.
Содержательно эта предпосылка важна с той же самой точки зрения, что и в условиях определенности она позволяет упростить анализ, отказавшись от рассмотрения поведения индивидов, обладающих лексикографическими предпочтениями. Например, покупка акций, облигаций или прочих товаров, чья покупка сопряжена с той или иной степенью неопределенности, сопровождается постоянным торгом между повышением надежностью компании и понижением уровня доходности ценных бумаг. Для индивида с лексикографическими предпочтениями и приоритетом безопасности вложений над экономической выгодой такого рода решение было бы невозможно.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.18.198 (0.006 с.) |

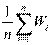 , стремящийся при n к величине математического ожидания денежного выигрыша
, стремящийся при n к величине математического ожидания денежного выигрыша



