
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обмен в условиях неопределенности.Содержание книги
Поиск на нашем сайте
а) риски L индивидуальные и негативно коррелированные Воспользуемся диаграммой Эджворта для анализа взаимодействия, возникающего между индивидами, столкнувшимися с независимыми негативно коррелированными рисками. Негативная коррелированность рисков означает, что в состоянии 2 потери терпит индивид 1, в то время как в состоянии 1 - индивид 2.
Обмен между индивидами взаимными обязательствами на случай наступления того или иного состояния(state--contigent claims to wealth) имеет смысл только до того момента, когда станет ясно, какое из двух возможных состояний реализовалось. Простоты ради будем полагать, что оба индивида первоначально располагают одинаковой суммой денег W0, и подвергаются одинаковому риску понести потери L. Подобные условия обусловливают равенство сторон диаграммы Эджворта (длина стороны квадрата равна 2 W0 - L).
То, что диаграмма Эджворта имеет квадратный вид, предполагает отсутствие общественных или системных рисков (уровень суммарного богатства в различных состояниях не варьируется). Если же говорить о рисках индивидуальных, то стремясь застраховать себя от них, индивиды могут заключить договор, в соответствии с которым "счастливчик" всякий раз делится с "неудачником" некоторой частью своего богатства.
При независимости функций полезности Бернулли от выпавшего состояния мира и совпадении оценок вероятности выпадения различных состояний, контрактная кривая будет представлять собой диагональ квадрата, совпадая с линиями уверенности агентов. Действительно, на линии уверенности w1 = w2, а, соответственно,
что обеспечивает совпадение предельных норм замещения с отношением вероятностей, а, следовательно, и друг с другом:
Это делает не просто возможным, но и оптимальным - предоставление всем индивидам полной страховки. Строго говоря, размеры платежей могут быть различными - все зависит от того, насколько сильны позиции каждой из сторон в ходе торга(т.е. то, что по английски называется a bargaining power - Рис.3.1.б).
В частности, при равном влиянии участников возможно заключение "справедливого" контракта, предполагающего изъятие у каждого из них денежной суммы, равной справедливой премии (сдвиг влево вверх вдоль линии постоянного ожидаемого выигрыша вплоть до точки на кривой уверенности). Подобное распределение предполагает, что первый индивид в любом из выпавших состояний получает сумму, равную математическому ожиданию выигрыша, т.е. W0 - Как бы то ни было, объединение риска в условиях, когда его осуществляют два не склонных к риску индивида с идентичными, но негативно коррелированными распределениями выигрышей, позволяет им обоим повысить уровень получаемой полезности.
б) риски индивидуальные - равные, но некоррелированные (независимые). Описанное выше объединение рисков имеет смысл и в случае независимых распределений выигрышей индивидов. Как и прежде, полагая равенство сумм W0, которыми первоначально располагают индивиды, и совпадение размеров возможных потерь L, предположим, что оба индивида сталкиваются с одинаковой вероятностью понести эти потери и для каждого из них она равна В результате возможно выпадение одного из четырех состояний:
Ожидаемая полезность каждого индивида взятого в отдельности, т.е. Еu(1) = может быть увеличена, в частности, если индивиды объединят свои риски, договорившись делить пополам суммарное богатство, выпадающее в каждом из состояний. В подобном случае ожидаемая полезность каждого индивида превысит первоначальный уровень(в предположении, что индивиды несклонны к риску, т.е. функция u(W) вогнута): Еu(2) = (1 -
Еu(2) - Еu(1) =
Увеличение числа индивидов повышает ожидаемую полезность каждого за счет сокращения возможных колебаний в уровне дохода(получение индивидом низкого или же высокого дохода в подобном случае менее вероятно, чем прежде, ибо неудача одного может быть смягчена выигрышем другого). Собственно, при сохранении прежнего математического ожидания выигрыша индивиды сталкиваются с меньшим разбросом выигрышей(т.е. менее рискованной игрой или игрой, стохастически второго рода доминирующей исходную). Например, если каждый из двух индивидов может с вероятностями 0.5 выиграть 1 или же не получить ничего, то объединение рисков или переход к лотерее 0.25 о 0 не сказавшись на уровне математического ожидания выигрыша, снизит дисперсию. Для не склонного к риску индивиду подобные изменения влекут за собой возрастание уровня ожидаемой полезности.
Возрастание числа индивидов, объединяющих свои риски, естественно, будет повышать уровень их ожидаемой полезности сходным образом.
Однако следует обратить внимание на то обстоятельство, что в подобной ситуации суммарное богатство варьируется в зависимости от того, какое из состояний реализовалось, и, следовательно, существуют социальные или системные риски. Предоставление полной страховки всем индивидам становится и не возможным и не эффективным. Невозможным - поскольку для этого нужно было бы иметь сумму вдвое превышающую математическое ожидание выигрыша каждого индивида, т.е. 2 (W0 -
Неэффективным - поскольку контрактная кривая (в общем случае, т.е. при несклонности к риску обоих контрагентов) более не совпадает с линиями уверенности.
Спрос на страхование. Как несклонность к риску влияет на поведение человека? Не склонный к риску человек интересуется не только ожидаемой величиной потерь, но и возможным размером потерь. Не склонный к риску человек сочтет ситуацию, которая чревата 10%-ным риском потери 20 тыс. долл. Более неблагоприятной, чем ситуация, чреватую 100%-ной вероятностью потери 2000 долл., хотя ожидаемая величина потерь во всех случаях одинаковая. Не склонные к риску стороны не любят неопределенности в отношении самой величины потерь.
Существует три способа, с помощью которых не склонный к риску человек может превратить неопределенный исход в определенный. Во-первых, он может купить рыночную страховку. Во-вторых, он может сам застраховать себя, например, отложив некоторую сумму денег, которая потребуется, чтобы покрыть потери. В-третьих, он может использовать возможности, предоставляемые договором, например, при покупке рискованных активов он может предложить за них более низкую цену.
Рассмотрим вариант с покупкой рыночной страховки. Покупка рыночной страховки
Владелец имеет автомобиль стоимостью 20000 долл. Вероятность угона автомобиля составляет 10%. В табл. 17 показано два возможных варианта благосостояния этого человека: со страховкой и без нее. Решение приобрести страховку не влияет на его ожидаемое благосостояние, оно по-прежнему составляет 18 тыс. долл.
Приобретение страховки не изменяет ожидаемого благосостояния, однако страховка способствует достижению более высокого уровня полезности для владельца автомобиля.
Владелец автомобиля — это сторона, не склонная к риску. Если риск несет не склонная к риску сторона, то это приведет к большему сокращению ожидаемой полезности дохода, чем несение риска менее склонной или нейтральной стороной. Поэтому та сторона, которая обнаруживает большую несклонность к риску, может заплатить менее несклонной или нейтральной к риску стороне за то, чтобы та приняла риск на себя, и обе стороны окажутся в более благоприятном положении, с точки зрения ожидаемой полезности. Владелец автомобиля будет готов заплатить 100 долл. за то, чтобы превратить неопределенное будущее в определенное, и его готовность платить говорит о том, что он не склонен к риску.
Страхование позволяет индивиду обменять риск больших потерь на определенность малых потерь.
Если имеются не склонные к риску стороны, то это означает, что распределение риска само по себе влияет на богатство общества. Предположим, что благосостояние общества — это сумма ожидаемых полезностей сторон. Перераспределение риска от не склонных к риску к нейтральным к риску сторонам приведет к повышению богатства общества.
Общественное благосостояние повышается не только когда риск полностью перекладывается с более несклонной к риску стороны на менее несклонную или нейтральную к риску сторону, но и когда риски делятся между не склонными к риску сторонами.
3. Теория игр. Дилемма заключенных. Равновесие в доминирующих стратегиях. Равновесие по Нэшу. Последовательные игры с совершенной информацией. Метод обратной индукции и common knowledge. Соображения, связанные с правомерностью применения метода обратной индукции. Простейшая модель торга (дележка доллара). Информационное множество. Усечение игры. Совершенное равновесие по Нэшу. Повторяемые игры. Сигнализирующие игры.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.234.68 (0.007 с.) |



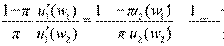
 L, где
L, где 
 0.5 о 1/2
0.5 о 1/2 



