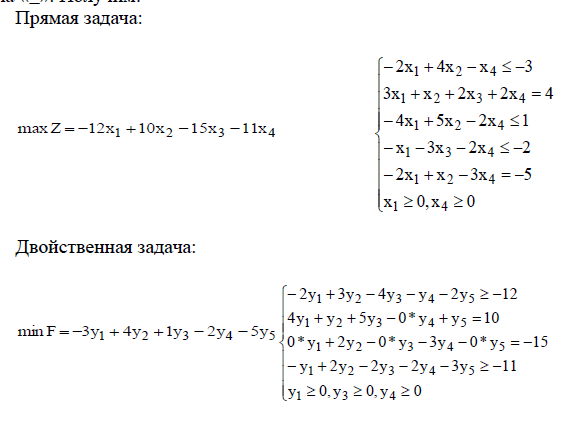Правила построения несимметричной двойственной задачи:

1) если на переменную xj прямой задачи наложено условие неотрицательности, то j-e условие системы ограничений двойственной задачи является неравенством;

2) если на переменную xj прямой задачи не наложено условие неотрицательности, то j-e условие системы ограничений двойственной задачи записывается в виде строгого равенства;

3) если в прямой задаче имеются ограничения равенства, то на соответствующие переменные двойственной задачи не накладывается условие неотрицательности.

15. Теоремы двойственности и их экономическое содержание.

Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем двойственности.

Основное неравенство теории двойственности: для любых допустимых решений x и y пары двойственных ЗЛП справедливо неравенство

1) Теорема существования (Малая теорема двойственности): чтобы прямая и двойственная задачи имели оптимальное решение необходимо и достаточно, чтобы существовали допустимые решения для каждой из них.

 

Кроме достаточного признака оптимальности взаимно двойственных задач существуют и другие важные соотношения между их решениями. Прежде всего возникают вопросы: всегда ли для каждой пары двойственных задач есть одновременно оптимальные решения; возможна ли ситуация, когда одна из двойственных задач имеет решение, а другая — нет. Ответ на эти вопросы дает следующая теорема.

2) I теорема двойственности: если одна из взаимно двойственных задач имеет оптимальное решение, то и вторая также имеет оптимальное решение, причѐм оптимальные значения их целевых функций равны

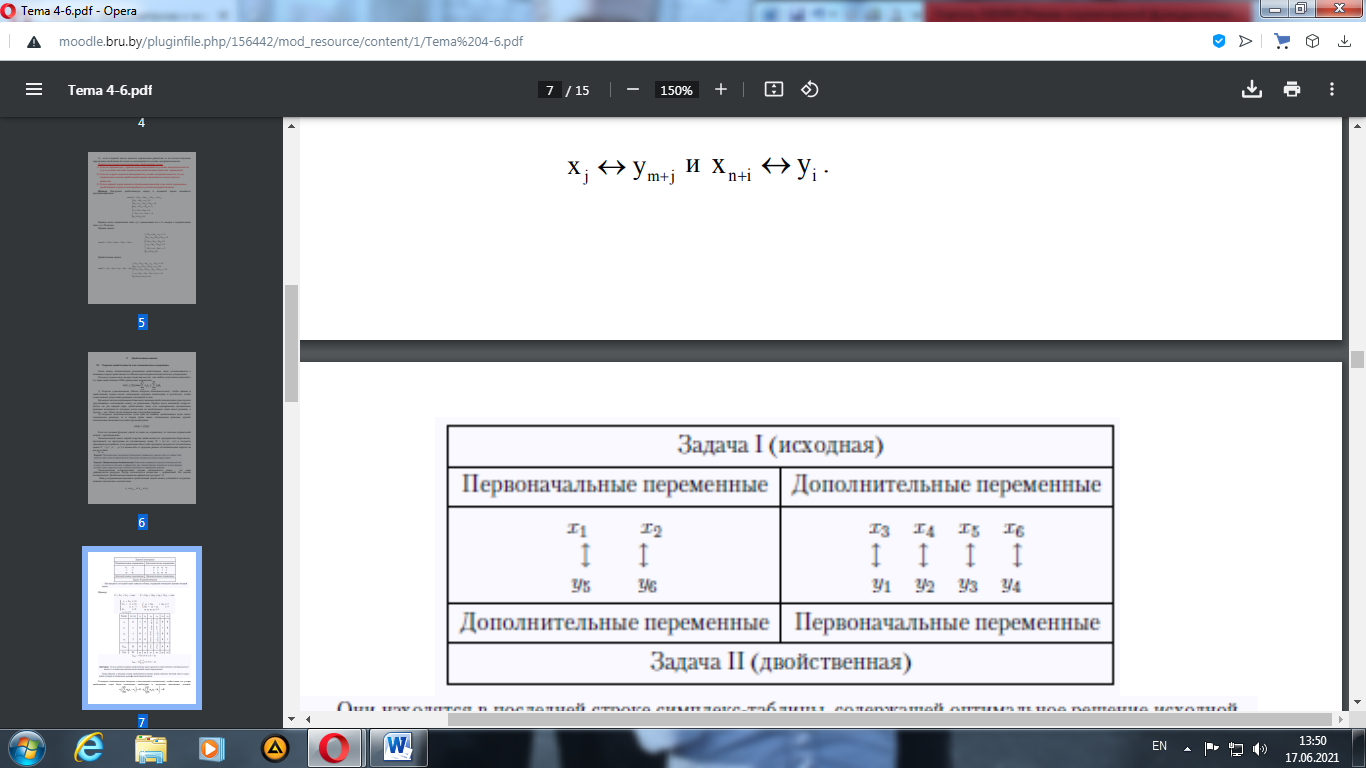
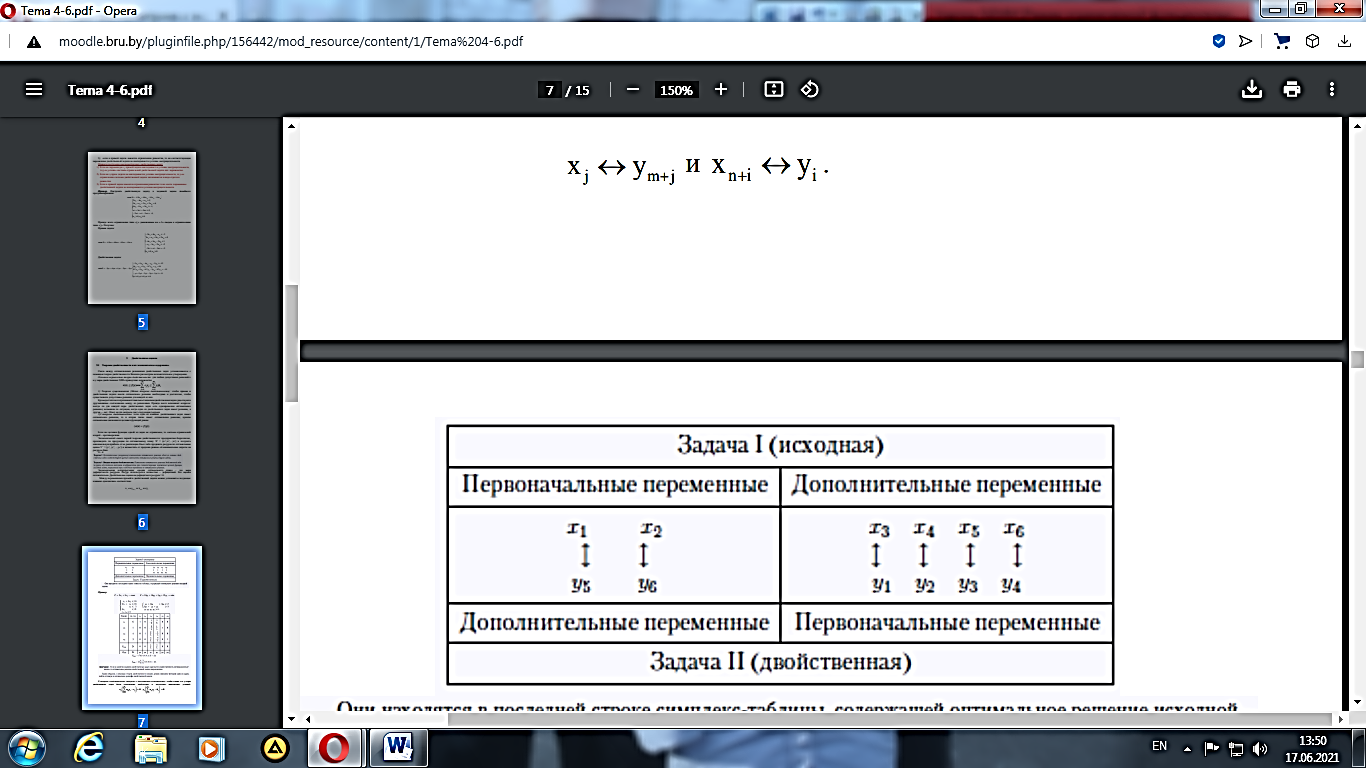
Если же целевая функция одной из задач не ограничена, то система ограничений второй – противоречива.

Экономический смысл первой теоремы двойственности: предприятию безразлично, производить ли продукцию по оптимальному плану X^∗ = (x1^∗,x2^∗,...,x_n^∗) и получить максимальную прибыль от ее реализации Fmax либо продавать ресурсы по оптимальным ценам Y^∗ = (y1^∗, y2^∗,...,y_n^∗) и возместить от продажи равные ей минимальные затраты на ресурсы Zmin.

Теорема3. Положительным (ненулевым) компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи.

Теорема4. Вторая теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.

Экономическая интерпретация: оценки оптимального плана – это мера дефицитности ресурсов. Ресурс используется полностью – дефицитный, его оценка положительна. Двойственная оценка недефицитного ресурса = 0. Между переменными прямой и двойственной задачи можно установить следующее взаимно однозначное соответствие

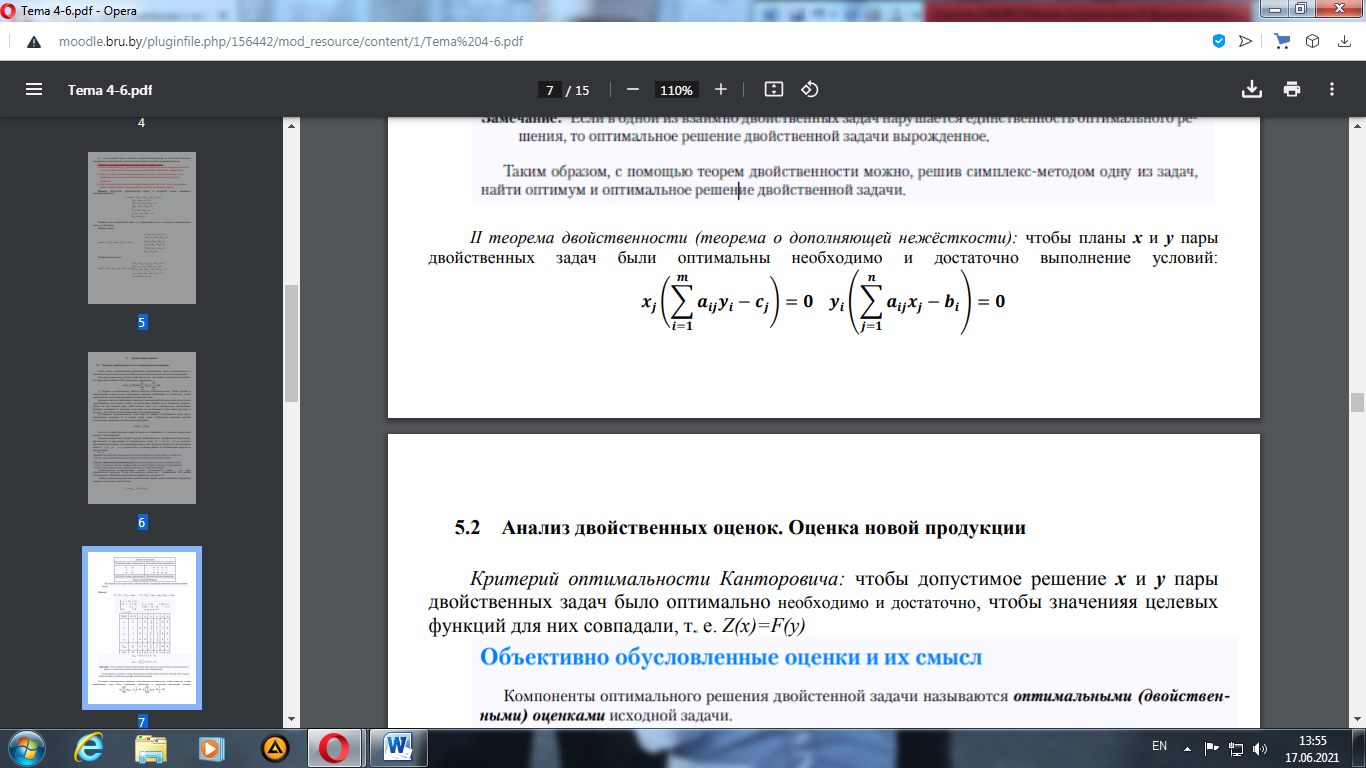
Таким образом, с помощью теорем двойственности можно, решив симплекс-методом одну из задач, найти оптимум и оптимальное решение двойственной задачи.

II теорема двойственности (теорема о дополняющей нежѐсткости): чтобы планы x и y пары двойственных задач были оптимальны необходимо и достаточно выполнение условий: