Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель и ее основные элементы.Содержание книги
Поиск на нашем сайте Модель и ее основные элементы.
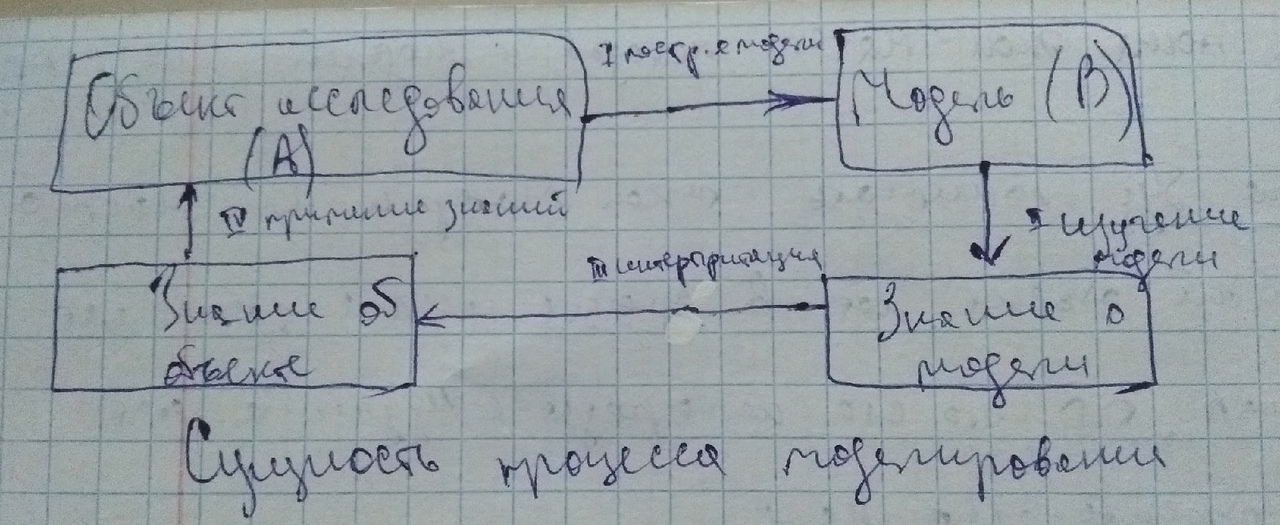
Под моделью будет пониматься такой материальный или мысленно представляемый объект, который в процессе иллюстрации заменяет объект-оригинал, таким образом, что его непосредственное изучение дает сведение об объекте-оригинале. Моделирование в таком случае представляет собой процесс построения, изучения и применение модели. Главная особенность моделирования состоит в том, что это метод опосредованного познания при помощи объектов-заменителей и т.о. включает 3 элемента: субъект исследования (исследователь), объект исследования, модель. Необходимость исследования с помощью модели определяется тем, что многие объекты (или проблемы, относящиеся к этим исследованиям) непосредственно исследовать нельзя или же эти исследования требуют слишком высоких затрат времени и средств.
Рисунок 1 – Основные этапы моделирования
I) Важнейшим является вопрос о необходимости и достаточности степени сходства оригинала и модели – этот вопрос требует детального анализа и решения в зависимости от конкретной ситуации. Очевидно, что утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестает быть моделью), так и в случае чрезмерного во всех существенных отношениях отличиях от оригинала.
Для понимания сущности моделирования важно не упускать из виду то, что моделирование – это не единственный источник знаний об объекте. Процесс моделирования, который «погружен» в более общий процесс познаний. Это обстоятельство должно учитываться не только на этапе построения модели, но и на завершающей стадии, когда происходит объединение и обобщение результатов исследования, полученных на основе многообразных средств познания.
Виды моделей.
Очевидно, что все существующие модели могут быть условно разделены на два класса: 1) модели материальные, т.е. объективно существующие (можно потрогать руками); 2) модели абстрактные, существующие в сознании человека. Одним из подклассов абстрактных моделей являются математические модели. Математические модели экономических процессов и называют экономико-математическими моделями (ЭММ). На бале исследования ЭММ реализуются прикладные программы, предназначенные для решения задач экономического анализа, планирования и управления. Математические модели являются важнейшим компонентом (наряду с БД, технологическими средствами, человеко-машинной интерпретацией), так называемых систем поддержки решений. Система поддержки решений – это человеко-машинная система, позволяющая использовать данные, знания, объект и субъект модели для анализа и решения слабо структурированных и неструктурированных проблем. Классифицируют ЭММ по различным признакам: 1) По целевому назначению: · теоретико-аналитические – предназначены для изучения общих закономерностей и свойств рассматриваемой экономической системы; · прикладные – используются для решения конкретных задач. 2) По уровням исследуемых экономических систем: · производственно-технические; · социально-технологические. 3) По характеру отражаемых причинно-следственных связей: · детерминированные модели (в них предполагаются жесткие функциональные связи между переменными); · недетерминированные (вероятностные, стохастические) – учитывают фактор неопределенности. Стохастические модели – модели, в которых допускается наличие случайных воздействий на исследуемые показатели и используются теории вероятностей и математической статистики. Теоретико-игровые модели – модели, в которых учитывается воздействие факторов, обладающих более высокой степенью неопределенности. 4) По способу отражения фактора времени: · статические – зависимости относятся к одному моменту иди периоду времени; · динамические – учитывается характер изменения процессов во времени. 5) По признаку способа отражения времени: · дискретные – модели, в которых время квантов (результат на каждую дату); · непрерывные – модели, в которых время рассматривается как непрерывный фактор. 6) По форме математической зависимости: · линейные – наиболее удобные для анализа, вследствие чего получили наибольшее распространение; · нелинейные. 7) По степени детализации: · агрегированные (макромодели) · детализированные (микромодели)
Признаки системы: 1) Целостность системы (систему нельзя считать работоспособной, если отсутствует хотя бы один из ее элементов). 2) Наличие цели и критериев исследования данного множества элементов. 3) Наличие более крупной, внешней по отношению к данной системе, т.н. «среды». 4) Возможность выделения в данной системе взаимосвязанных частей подсистемы. Основным методом исследования систем является метод моделирования, т.е. способ технологического анализа и практического действия, направленный на разработку и исследование модели. При этом под моделью понимается образ реального объекта (или процесса) в реальной форме (или описанной знаковыми средствами на каком-либо языке), отражающий существенные черты моделируемого объекта и замещающий его в ходе исследования и управления. Метод моделирования основывается на принципе аналогии, т.е. возможности изучения реального объекта не непосредственно, а через рассмотрение подобного ему и более доступного объекта (его модели). В дальнейшем будет рассматриваться только ЭММ. Практическими задачами ЭММ являются: 1) анализ экономических объектов и процессов; 2) экономическое прогнозирование, предвидение развития экономических процессов; 3) выработка управленческих решений на всех уровнях хозяйственной иерархии.
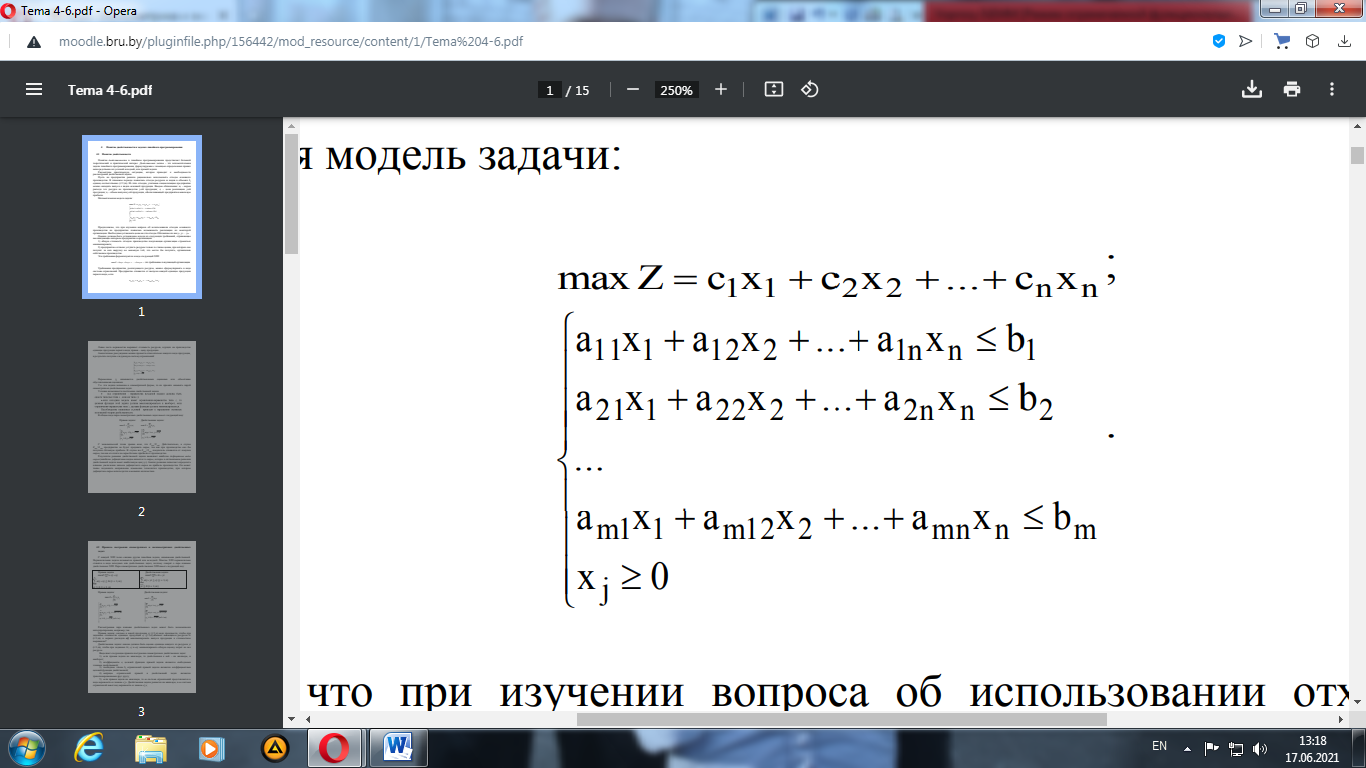
Важнейшим понятием при ЭММ, как и при всяком моделировании, является понятие адекватности модели, т.е. соотношение модели объекту или процессу (а именно - соответствие модели тем свойствам, которые считаются существенными для исследования). Проверка адекватности ЭММ является серьезной проблемой, тем более, ее осложняет трудность измерения экономических величин. Однако, без такой проверки применение результатов моделирования в управленческих решениях может оказаться не только бесполезным, но и принести существенный вред. Социально-экономические системы открыты, как правило, к так называемым «сложным системам». Сложные системы (в экономике) обладают рядом свойств, которые необходимо учитывать при их моделировании, иначе невозможно говорить об адекватности построенной экономической модели. Важнейшие из них: - энерджентность – проявление целостности систем, т.е. наличие у экономической системы таких свойств, которые не присущи ни одному из составляющих систему элементов, взятые в отдельности вне системы. - массовый характер экономических моделей и процессов. - динамичность экономических процессов – заключается в изменении качества и структуры экономических систем под влиянием среды (внешних факторов); - случайность и неопределенность в развитии экономических явлений. - невозможность изолировать взятые из экономических систем явления и процессы от окружающей среды, чтобы наблюдать и исследовать их в чистом виде. - активная реакция на появление новых факторов, способность социально-экономических систем к активным, не всегда предсказуемым действиям в зависимости от отношений системы к этим факторам, способам и методам их воздействия. Линейное программирование Математическое программирование («планирование») – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи (РЗ) возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности. Линейное программирование – направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности. Программирование здесь должно интерпретироваться как планирование, формирование планов, разработка программы действий. К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов. Круг задач, решаемых при помощи методов ЛП достаточно широк. Это, например: - задача об оптимальном использовании ресурсов при производственном планировании; - задача о смесях (планирование состава продукции); - задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или «задача о рюкзаке»); - транспортные задачи (анализ размещения предприятия, перемещение грузов). Линейное программирование – наиболее разработанный и широко применяемый раздел математического программирования (кроме того, сюда относят: целочисленное, динамическое, нелинейное, параметрическое программирование). Это объясняется следующим: - математические модели большого числа экономических задач линейны относительно искомых переменных; - данный тип задач в настоящее время наиболее изучен. Для него разработаны специальные методы, с помощью которых эти задачи решаются, и соответствующие программы для ЭВМ; - многие задачи линейного программирования, будучи решенными, нашли широкое применение; некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования. Таким образом, в зависимости от вида целевой функции и области допустимых решений выделяют следующие типы задач: - ЗЛП: целевая функция и уравнения, задающие ОДР, линейны; - задачи нелинейного программирования, если форма ц.ф. или область допустимых планов носит нелинейный характер; - задачи целочисленного программирования, если ставится условие целочисленности управляемых переменных. По типу решаемых задач методы ЛП разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые ЗЛП. Специальные учитывают особенности модели задачи, ее целевой функции и системы ограничений. Главная особенность задач линейного программирования заключается в том, что экстремум целевой функции находится на границе области допустимых решений.
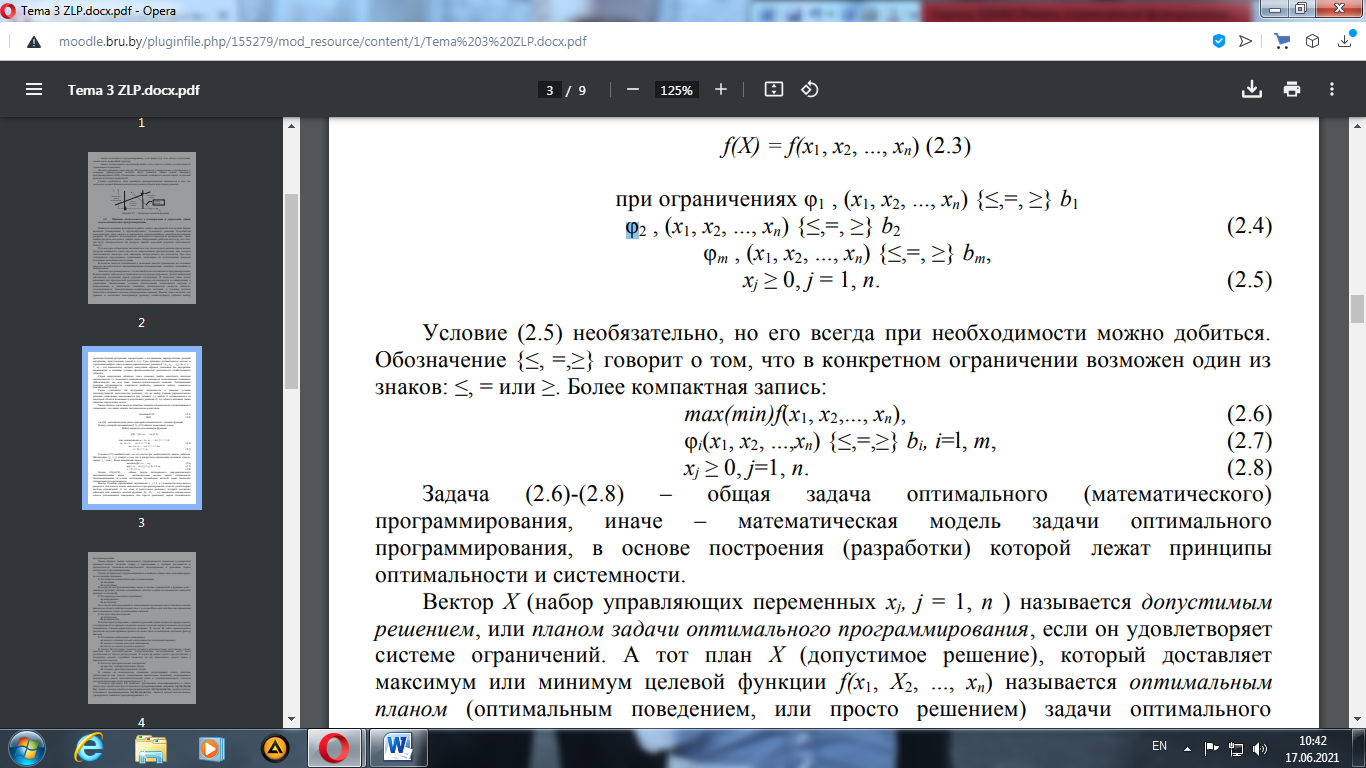
6. Принцип оптимальности в планировании и управлении, общая задача оптимального программирования. Наиболее сложными функциями в работе любого предприятия или частной фирмы являются планирование и прогнозирование. Успешность решения большинства экономических задач зависит от наилучшего, наивыгоднейшего способа использования ресурсов. В процессе экономической деятельности приходится распределять такие важные ресурсы, как деньги, товары, сырье, оборудование, рабочую силу и др. и от того, как будут распределяться эти ресурсы, зависит конечный результат деятельности, бизнеса. Суть методов оптимизации заключается в том, что, исходя из наличия определенных ресурсов, выбирается такой способ их использования (распределения), при котором обеспечивается максимум (или минимум) интересующего нас показателя. При этом учитываются определенные ограничения, налагаемые на использование ресурсов условиями экономической ситуации. В качестве методов оптимизации в экономике находят применение все основные разделы математического программирования (планирования): линейное, нелинейное и динамическое. Линейное программирование - это частный раздел оптимального программирования (раздел прикладной математики, изучающий задачи условной оптимизации). В экономике такие задачи возникают при практической реализации принципа оптимальности в планировании и управлении. Необходимым условием использования оптимального подхода к планированию и управлению (принципа оптимальности) является гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать планово-управленческие решения. Суть принципа оптимальности состоит в стремлении выбрать такое планово-управленческое решение X = (х1, х2,..., хп), которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта. Слова «наилучшим образом» здесь означают выбор некоторого критерия оптимальности, т.е. некоторого экономического показателя, позволяющего сравнивать эффективность тех или иных планово-управленческих решений. Традиционные критерии оптимальности: «максимум прибыли», «минимум затрат», «максимум рентабельности» и др. Слова «учитывало бы внутренние возможности и внешние условия производственной деятельности» означают, что на выбор планово-управленческого решения (поведения) накладывается ряд условий, т.е. выбор X осуществляется из некоторой области возможных (допустимых) решений D; эту область называют также областью определения задачи. Таким образом, реализовать на практике принцип оптимальности в планировании и управлении - это значит решить экстремальную задачу вида:
где f(X) - математическая запись критерия оптимальности (целевая функция). Задачу условной оптимизации (2.1), (2.2) обычно записывают в виде: Найти максимум или минимум функции
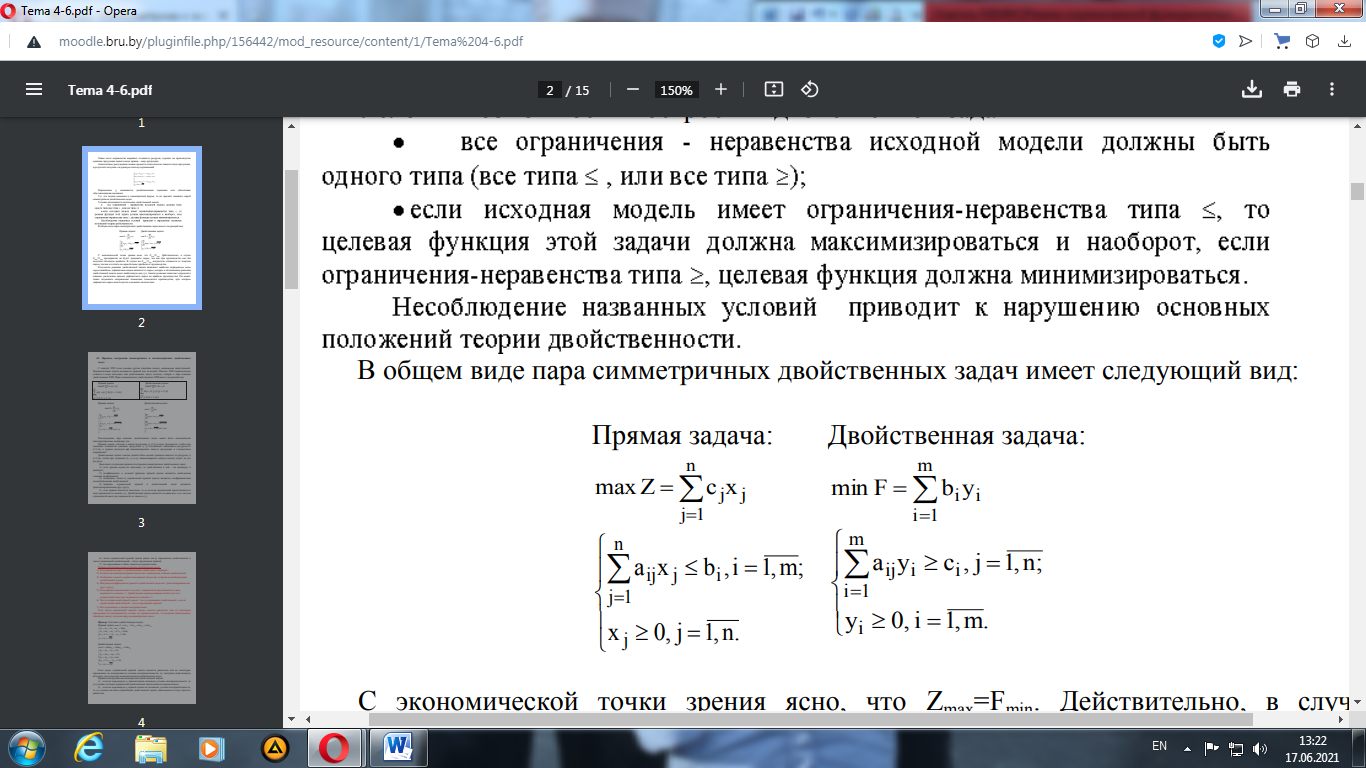
Условие (2.5) необязательно, но его всегда при необходимости можно добиться. Обозначение {≤, =,≥} говорит о том, что в конкретном ограничении возможен один из знаков: ≤, = или ≥. Более компактная запись:
Задача (2.6) - (2.8) – общая задача оптимального (математического) программирования, иначе – математическая модель задачи оптимального программирования, в основе построения (разработки) которой лежат принципы оптимальности и системности. Вектор X (набор управляющих переменных xj, j = 1, п) называется оптимальным решением, если он удовлетворяет системе ограничений (допустимый план) + доставляет максимум или минимум целевой функции f(x1, Х2,..., хп) (оптимальный план – решение задачи оптимального программирования). Задачи оптимального программирования в наиболее общем виде классифицируют по следующим признакам. 1. По характеру взаимосвязи между переменными: а) линейные, б) нелинейные. 2. По характеру изменения переменных: а) непрерывные, б) дискретные. В случае а) значения каждой из управляющих переменных могут заполнять сплошь некоторую область действительных чисел; в случае б) все или хотя бы одна переменная могут принимать только целочисленные значения. 3. По учету фактора времени: а) статические, б) динамические. В задачах а) моделирование и принятие решений осуществляются в предположении о независимости от времени элементов модели в течение периода времени, на который принимается планово-управленческое решение. В случае б) такое предположение достаточно аргументированно принято не может быть и необходимо учитывать фактор времени. 4. По наличию информации о переменных: а) задачи в условиях полной определенности (детерминированные), б) задачи в условиях неполной информации, в) задачи в условиях неопределенности. В задачах б) отдельные элементы являются вероятностными величинами, однако известны или дополнительными статистическими исследованиями могут быть установлены их законы распределения. В случае в) можно сделать предположение о возможных исходах случайных элементов, но нет возможности сделать вывод о вероятностях исходов. 5. По числу критериев оценки альтернатив: а) простые, однокритериальные задачи, б) сложные, многокритериальные задачи. В задачах а) экономически приемлемо использование одного критерия оптимальности или удается специальными процедурами (например, «взвешиванием приоритетов») свести многокритериальный поиск к однокритериальному. Сочетание признаков 1-5 позволяет группировать (классифицировать) в самом общем виде задачи и методы оптимального программирования, например: 1а) 2а) 3а) 4а) 5а) - задачи и методы линейного программирования, 1б) 2а) 3а) 4а) 5а) - задачи и методы нелинейного программирования, 1а) 2б) 3а) 4а) 5а) - задачи и методы целочисленного (дискретного) линейного программирования и т.д. Понятие двойственности. Двойственная задача - это вспомогательная задача линейного программирования, формулируемая с помощью определенных правил непосредственно из условий исходной, или прямой задачи. Рассмотрим практическую ситуацию, которая приводит к необходимости рассмотрения двойственной задачи.
Предположим, что при изучении вопроса об использовании отходов основного производства на предприятии появилась возможность реализации их некоторой организации. Необходимо установить цены на эти отходы. Обозначим их как y1, y2... ym. Оценки должны быть установлены исходя из следующих требований, отражающие несовпадающие интересы предприятия и организации: 1) общую стоимость отходов производства покупающая организация стремиться минимизировать; 2) предприятие согласно уступить ресурсы только по таким ценам, при которых оно получит за них выручку не меньшую той, что могло бы получить, организовав собственное производство. Эти требования формализуются в виде следующей ЗЛП:
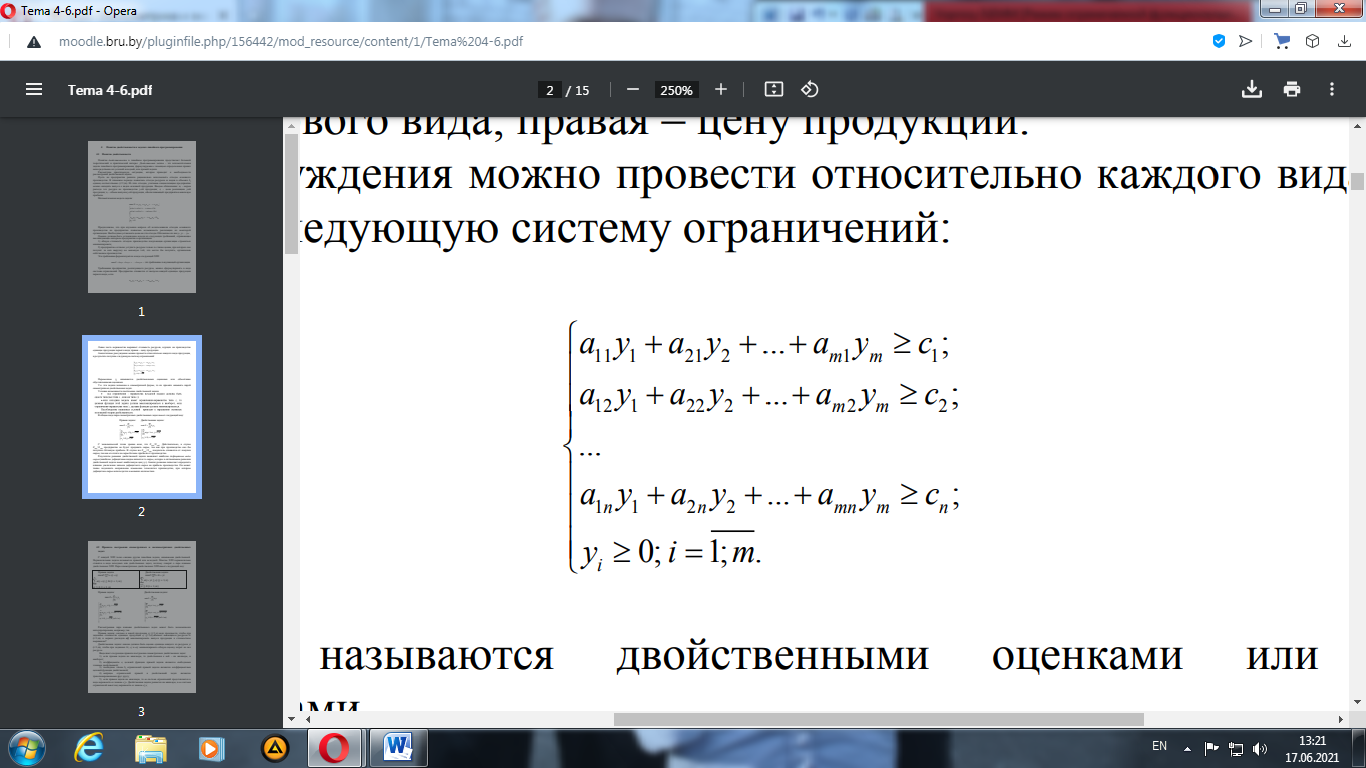
Требования предприятия, реализующего ресурсы, можно сформулировать в виде системы ограничений. Предприятие откажется от выпуска каждой единицы продукции первого вида, если Левая часть неравенства выражает стоимость ресурсов, идущих на производство единицы продукции первого вида; правая – цену продукции. Аналогичные рассуждения можно провести относительно каждого вида продукции, в результате получим следующую систему ограничений:
Переменные yi называются двойственными оценками. Т.к. эти задачи записаны в симметричной форме, то их принято называть парой симметричных двойственных задач. Условия возможности построения двойственной задачи:
Если среди ограничений прямой задачи имеются равенства или на некоторые переменные не накладывается условие неотрицательности, то, построив двойственную ей задачу, получим пару несимметричных двойственных задач. Решение.
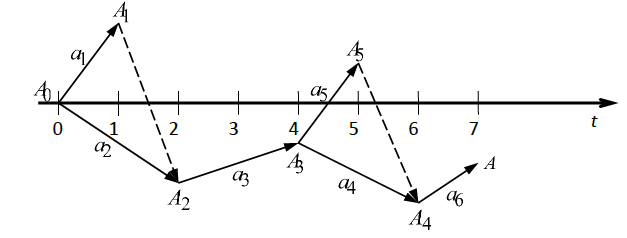
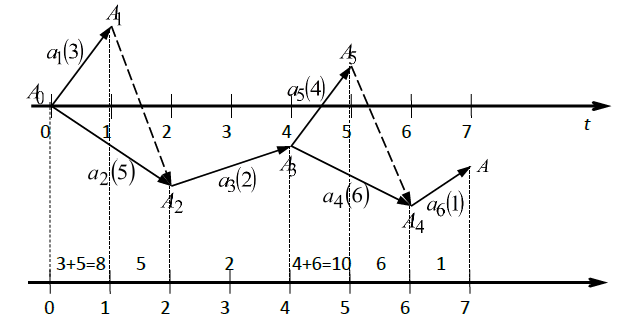
Рисунок 9.3 - Временной сетевой график Здесь критическими работами являются а2, а3, а4, а5. Тогда критическое время выполнения проекта будет: T кр = t 2 + t 3 + t 4 + t 6 = 20 + 20 + 20 +10 = 70. На рисунке 9.3 построен временной сетевой график. Для определения числа исполнителей, необходимого для выполнения всего комплекса работ, построим шкалу потребления ресурса. Обозначим на временном сетевом графике число исполнителей для каждой работы (в скобках около наименования работы, т.е. ai (ri)). На ось времени Оt сетевого графика проектируют пунктирными линиями начальные и конечные точки всех работ и получают промежутки постоянства интенсивности потребления ресурса. Суммарную потребность в ресурсе в данном временном промежутке определяют, суммируя интенсивности всех работ, расположенных над этим промежутком (см. рисунок 9.4).
Рисунок 9.4 – Расчет потребности в ресурсе на временном сетевом графике Максимальное число исполнителей (10 человек) требуется на промежутке времени [40,50]. Следовательно, R=10. Таким образом, для выполнения данного проекта потребуется минимум 10 человек. Основные понятия теории игр. Классификация игр «ИГРА» - это упрощенная, схематизированная модель конфликтной ситуации, который позволяет отвлечься от второстепенных факторов, что значительно упрощает ее анализ. Теория игр – математическая теория конфликтных ситуаций. Игры бывают ПАРНЫЕ и МНОЖЕСТВЕННЫЕ. В первом случае число участников равно двум, во втором – более двух. Игры, в которых целью каждого участника является получение по возможности большего индивидуального выигрыша, называются бескоалиционными в отличие от коалиционных (кооперативных), в которых действия игроков направлены на максимизацию выигрышей коллективов (коалиции (кооперации)) без дальнейшего разделения выигрыша между участниками, когда их цели совпадают. Коалиции бывают постоянные или временные. Игра с двумя постоянными коалициями превращается в парную. Наибольшее практическое значение имеют парные игры. Пусть имеется парная игра, в которой участвуют два игрока А и В с противоположными интересами. Под ИГРОЙ понимается мероприятие, состоящее из ряда действий (или ходов) сторон А и В. Каждая партия в игре заканчивается выигрышем только одного из игроков. Чтобы игра могла быть подвергнута математическому анализу, необходимо четко сформулировать ПРАВИЛА ИГРЫ – это система условий, регламентирующая: 1) возможные варианты действий игроков; 2) объем информации каждой стороны о поведении другой; 3) исход игры, к которому приводит каждая совокупность ходов. Исход игры должен оцениваться КОЛИЧЕСТВЕННО. Если это не вытекает из сути игры, то можно условно выразить исход игры числом. Например, в шахматной игре выигрышу приписывается значение 1, проигрышу – 0, ничьей – 0,5. Игра называется ИГРОЙ С НУЛЕВОЙ СУММОЙ, если один игрок выигрывает ровно столько, сколько проигрывает другой, т.е. сумма выигрышей сторон равна нулю. Таким образом, в игре с нулевой суммой интересы игроков прямо противоположны. Если а - выигрыш игрока А, b - выигрыш игрока В, то a+b=0, следовательно a=-b. Поэтому при анализе такой игры достаточно рассмотреть выигрыш одного из игроков. Пример игры с нулевой суммой – шахматная игра, а игры с ненулевой суммой – карточная игра с банкиром, который держит банк и забирает часть выигрыша себе. Игра по времени разворачивается в виде последовательности ХОДОВ. Ход (в теории игр) – это выбор одного из предусмотренных правилами игры действий и его осуществление. Ходы бывают личные и случайные. При личном ходе игрок сам принимает решение об осуществлении одного из возможных вариантов действий. При случайном ходе такое решение принимается на основе какого-либо механизма случайного выбора (бросание монеты, выбор карты из перетасованной колоды, датчик случайных чисел и т.п.). Некоторые игры состоят только из случайных ходов (чисто азартные игры), или только из личных ходов (шахматы и т.д.), либо содержат как личные, так и случайные ходы (карточные игры). Теория игр занимается анализом только тех игр, которые содержат личные ходы. Ее задача – дать рекомендации игрокам при выборе их личных ходов в зависимости от ситуации, сложившейся в процессе игры. СТРАТЕГИЕЙ игрока называется система правил, однозначно определяющих выбор поведения игрока на каждом личном ходе в зависимости от ситуации, сложившейся в процессе игры. Обычно, принимая участие в игре, игрок не следует каким-либо жестким, фиксированным правилам: выбор при каждом личном ходе принимается им в ходе игры в зависимости от конкретной сложившейся ситуации. Однако теоретически дело не изменится, если мы представим себе, что все эти решения приняты игроком заранее («если сложится такая-то ситуация, то я поступлю так-то...»). В принципе это возможно при любой игре. Если такая система решений будет принята, это будет означать, что игрок выбрал определенную стратегию. Теперь он может не участвовать в игре лично, а заменить свое участие списком правил, которые за него будет применять незаинтересованное лицо. Именно так играет в шахматы ЭВМ. Игра называется КОНЕЧНОЙ, если у каждого игрока имеется только конечное число стратегий, и БЕСКОНЕЧНОЙ, если хотя бы у одного из игроков имеется бесконечное число стратегий. Целью теории игр является определение оптимальной стратегии для каждого из игроков. ОПТИМАЛЬНОЙ СТРАТЕГИЕЙ игрока называется такая стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш (или минимально возможный средний проигрыш). При выборе этой стратегии основой рассуждения является предположение, что противник по меньшей мере так же разумен, как и мы сами, и делает все для того, чтобы помешать нам добиться своей цели. Таким образом в теории игр все рекомендации определяются без учета возможных просчетов и ошибок игроков, а также элементов азарта и риска. Игра называется игрой с ПОЛНОЙ ИНФОРМАЦИЕЙ, если результаты случайных ходов и предыдущих личных ходов полностью известны каждому игроку. В противном случае игра является игрой с НЕПОЛНОЙ ИНФОРМАЦИЕЙ. Например, шахматы и шашки – игры с полной информацией, а карточные игры – с неполной информацией. Модель и ее основные элементы.
Под моделью будет пониматься такой материальный или мысленно представляемый объект, который в процессе иллюстрации заменяет объект-оригинал, таким образом, что его непосредственное изучение дает сведение об объекте-оригинале. Моделирование в таком случае представляет собой процесс построения, изучения и применение модели. Главная особенность моделирования состоит в том, что это метод опосредованного познания при помощи объектов-заменителей и т.о. включает 3 элемента: субъект исследования (исследователь), объект исследования, модель. Необходимость исследования с помощью модели определяется тем, что многие объекты (или проблемы, относящиеся к этим исследованиям) непосредственно исследовать нельзя или же эти исследования требуют слишком высоких затрат времени и средств.
Рисунок 1 – Основные этапы моделирования
I) Важнейшим является вопрос о необходимости и достаточности степени сходства оригинала и модели – этот вопрос требует детального анализа и решения в зависимости от конкретной ситуации. Очевидно, что утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестает быть моделью), так и в случае чрезмерного во всех существенных отношениях отличиях от оригинала.
Для понимания сущности моделирования важно не упускать из виду то, что моделирование – это не единственный источник знаний об объекте. Процесс моделирования, который «погружен» в более общий процесс познаний. Это обстоятельство должно учитываться не только на этапе построения модели, но и на завершающей стадии, когда происходит объединение и обобщение результатов исследования, полученных на основе многообразных средств познания.
Виды моделей.
Очевидно, что все существующие модели могут быть условно разделены на два класса: 1) модели материальные, т.е. объективно существующие (можно потрогать руками); 2) модели абстрактные, существующие в сознании человека. Одним из подклассов абстрактных моделей являются математические модели. Математические модели экономических процессов и называют экономико-математическими моделями (ЭММ). На бале исследования ЭММ реализуются прикладные программы, предназначенные для решения задач экономического анализа, планирования и управления. Математические модели являются важнейшим компонентом (наряду с БД, технологическими средствами, человеко-машинной интерпретацией), так называемых систем поддержки решений. Система поддержки решений – это человеко-машинная система, позволяющая использовать данные, знания, объект и субъект модели для анализа и решения слабо структурированных и неструктурированных проблем. Классифицируют ЭММ по различным признакам: 1) По целевому назначению: · теоретико-аналитические – предназначены для изучения общих закономерностей и свойств рассматриваемой экономической системы; · прикладные – используются для решения конкретных задач. 2) По уровням исследуемых экономических систем: · производственно-технические; · социально-технологические. 3) По характеру отражаемых причинно-следственных связей: · детерминированные модели (в них предполагаются жесткие функциональные связи между переменными); · недетерминированные (вероятностные, стохастические) – учитывают фактор неопределенности. Стохастические модели – модели, в которых допускается наличие случайных воздействий на исследуемые показатели и используются теории вероятностей и математической статистики. Теоретико-игровые модели – модели, в которых учитывается воздействие факторов, обладающих более высокой степенью неопределенности. 4) По способу отражения фактора времени: · статические – зависимости относятся к одному моменту иди периоду времени; · динамические – учитывается характер изменения процессов во времени. 5) По признаку способа отражения времени: · дискретные – модели, в которых время квантов (результат на каждую дату); · непрерывные – модели, в которых время рассматривается как непрерывный фактор. 6) По форме математической зависимости: · линейные – наиболее удобные для анализа, вследствие чего получили наибольшее распространение; · нелинейные. 7) По степени детализации: · агрегированные (макромодели) · детализированные (микромодели)
|
||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.016 с.) |




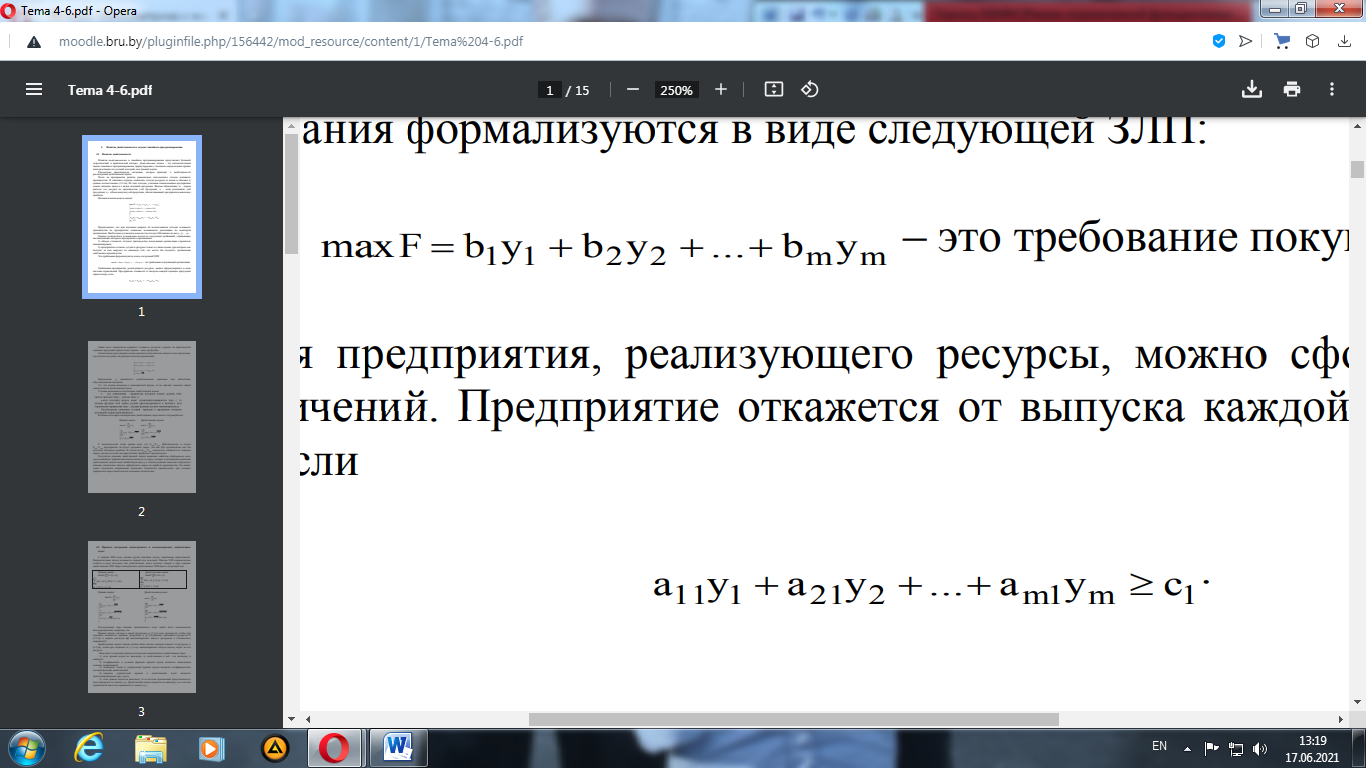 – это требование покупающей организации.
– это требование покупающей организации.