Этапы экономико-математического моделирования

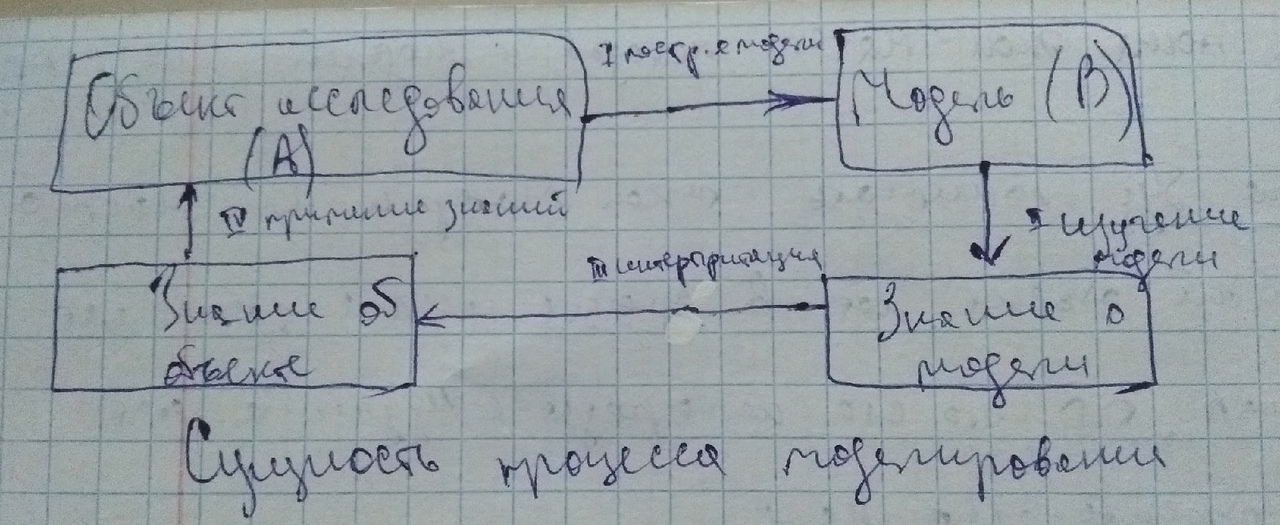
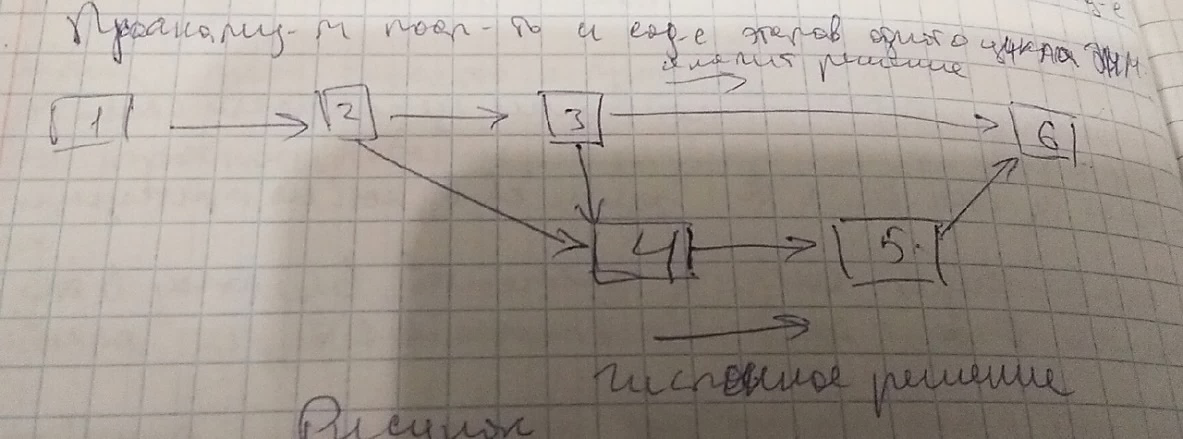
Основные этапы моделирования рассмотрены выше (рисунок 1). В различных отраслях знаний они приобретают свои специфические черты. Проанализируем последовательность и содержание этапов одного цикла ЭММ.

1) Постановка проблемы и ее анализ.

Главное – четко сформулировать сущность проблемы и определить приемлемые допущения;

2) Построение математической модели – это формализация задачи, т.е. выражение ее в виде математических зависимостей и отношений.

3) Математический анализ модели.

Цель: выявление общих свойств и характеристик модели. Применяются чисто математические методы исследования, наиболее важный момент – доказательство существования решений в сформированной модели, если удается доказать, что задача не имеет решения, то необходимость в последующей работе по данному варианту моделей отпадает – следует скорректировать либо постановку задачи, либо способы ее математической формулировки.

4) Подготовка исходной информации – численное моделирование определяет жесткие требования к исходной информации, в то время как имеющиеся возможности получения информации существенно ограничивают выбор исходных моделей (при этом принимается во внимание возможность не только подготовки информации (за определенный срок), но и затраты на подготовку соответствующих массивов). Эти затраты не должны превышать эффекта от использования информации.

5) Численное решение – составление алгоритмов разработки программ и непосредственно проведения расчетов на ЭММ.

6) Анализ результатов и их применение – проверяется правильность, полнота и степень практической применимости полученных результатов.

Определим, как соотносятся между собой общая схема процессов моделирования (рис. 1) и этапы ЭММ.

(1-5) – более детализированный характер процессов ЭМ-исследования, по сравнению с общей схемой;

(1-2) – этап I общей схемы;

(3-5) – этап II;

(6) – этап III и IV.

Линейное программирование

Математическое программирование («планирование») – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи (РЗ) возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности.

Линейное программирование – направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности.

Программирование здесь должно интерпретироваться как планирование, формирование планов, разработка программы действий. К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.

Круг задач, решаемых при помощи методов ЛП достаточно широк. Это, например:

- задача об оптимальном использовании ресурсов при производственном планировании;

- задача о смесях (планирование состава продукции);

- задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или «задача о рюкзаке»);

- транспортные задачи (анализ размещения предприятия, перемещение грузов).

Линейное программирование – наиболее разработанный и широко применяемый раздел математического программирования (кроме того, сюда относят: целочисленное, динамическое, нелинейное, параметрическое программирование). Это объясняется следующим:

- математические модели большого числа экономических задач линейны относительно искомых переменных;

 - данный тип задач в настоящее время наиболее изучен. Для него разработаны специальные методы, с помощью которых эти задачи решаются, и соответствующие программы для ЭВМ;

- многие задачи линейного программирования, будучи решенными, нашли широкое применение; некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.

Таким образом, в зависимости от вида целевой функции и области допустимых решений выделяют следующие типы задач:

- ЗЛП: целевая функция и уравнения, задающие ОДР, линейны;

- задачи нелинейного программирования, если форма ц.ф. или область допустимых планов носит нелинейный характер;

- задачи целочисленного программирования, если ставится условие целочисленности управляемых переменных.

По типу решаемых задач методы ЛП разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые ЗЛП. Специальные учитывают особенности модели задачи, ее целевой функции и системы ограничений.

Главная особенность задач линейного программирования заключается в том, что экстремум целевой функции находится на границе области допустимых решений.

6. Принцип оптимальности в планировании и управлении, общая задача оптимального программирования.

Наиболее сложными функциями в работе любого предприятия или частной фирмы являются планирование и прогнозирование. Успешность решения большинства экономических задач зависит от наилучшего, наивыгоднейшего способа использования ресурсов. В процессе экономической деятельности приходится распределять такие важные ресурсы, как деньги, товары, сырье, оборудование, рабочую силу и др. и от того, как будут распределяться эти ресурсы, зависит конечный результат деятельности, бизнеса.

Суть методов оптимизации заключается в том, что, исходя из наличия определенных ресурсов, выбирается такой способ их использования (распределения), при котором обеспечивается максимум (или минимум) интересующего нас показателя. При этом учитываются определенные ограничения, налагаемые на использование ресурсов условиями экономической ситуации.

В качестве методов оптимизации в экономике находят применение все основные разделы математического программирования (планирования): линейное, нелинейное и динамическое.

Линейное программирование - это частный раздел оптимального программирования (раздел прикладной математики, изучающий задачи условной оптимизации). В экономике такие задачи возникают при практической реализации принципа оптимальности в планировании и управлении. Необходимым условием использования оптимального подхода к планированию и управлению (принципа оптимальности) является гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать планово-управленческие решения.

Суть принципа оптимальности состоит в стремлении выбрать такое планово-управленческое решение X = (х1, х2,..., хп), которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.

Слова «наилучшим образом» здесь означают выбор некоторого критерия оптимальности, т.е. некоторого экономического показателя, позволяющего сравнивать эффективность тех или иных планово-управленческих решений. Традиционные критерии оптимальности: «максимум прибыли», «минимум затрат», «максимум рентабельности» и др.

Слова «учитывало бы внутренние возможности и внешние условия производственной деятельности» означают, что на выбор планово-управленческого решения (поведения) накладывается ряд условий, т.е. выбор X осуществляется из некоторой области возможных (допустимых) решений D; эту область называют также областью определения задачи.

Таким образом, реализовать на практике принцип оптимальности в планировании и управлении - это значит решить экстремальную задачу вида:

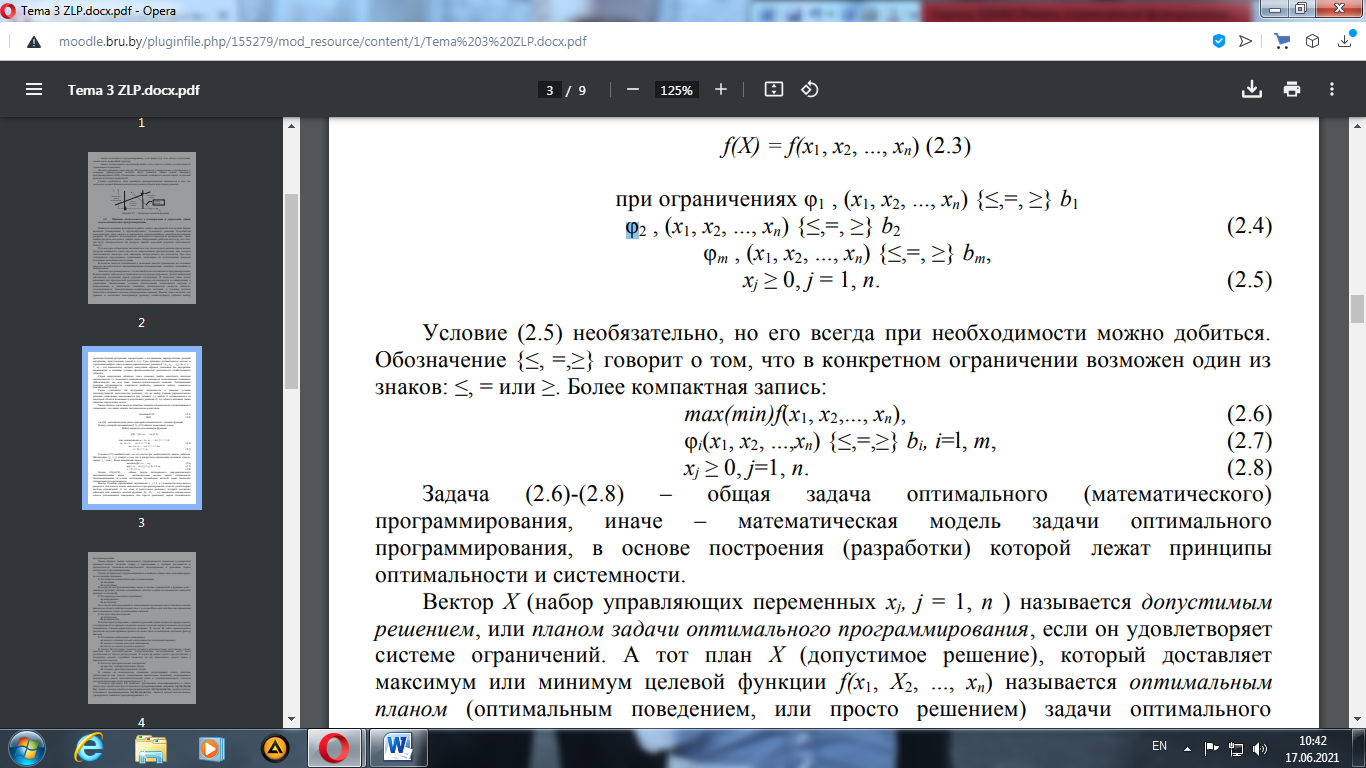
где f(X) - математическая запись критерия оптимальности (целевая функция).

Задачу условной оптимизации (2.1), (2.2) обычно записывают в виде:

Найти максимум или минимум функции

Условие (2.5) необязательно, но его всегда при необходимости можно добиться. Обозначение {≤, =,≥} говорит о том, что в конкретном ограничении возможен один из знаков: ≤, = или ≥. Более компактная запись:

Задача (2.6) - (2.8) – общая задача оптимального (математического) программирования, иначе – математическая модель задачи оптимального программирования, в основе построения (разработки) которой лежат принципы оптимальности и системности.

Вектор X (набор управляющих переменных xj, j = 1, п) называется оптимальным решением, если он удовлетворяет системе ограничений (допустимый план) + доставляет максимум или минимум целевой функции f(x1, Х2,..., хп) (оптимальный план – решение задачи оптимального программирования).

Задачи оптимального программирования в наиболее общем виде классифицируют по следующим признакам.

1. По характеру взаимосвязи между переменными: а) линейные, б) нелинейные.    

2. По характеру изменения переменных: а) непрерывные, б) дискретные.

В случае а) значения каждой из управляющих переменных могут заполнять сплошь некоторую область действительных чисел; в случае б) все или хотя бы одна переменная могут принимать только целочисленные значения.

3. По учету фактора времени: а) статические, б) динамические. В задачах а) моделирование и принятие решений осуществляются в предположении о независимости от времени элементов модели в течение периода времени, на который принимается планово-управленческое решение. В случае б) такое предположение достаточно аргументированно принято не может быть и необходимо учитывать фактор времени.

 4. По наличию информации о переменных: а) задачи в условиях полной определенности (детерминированные), б) задачи в условиях неполной информации, в) задачи в условиях неопределенности. В задачах б) отдельные элементы являются вероятностными величинами, однако известны или дополнительными статистическими исследованиями могут быть установлены их законы распределения. В случае в) можно сделать предположение о возможных исходах случайных элементов, но нет возможности сделать вывод о вероятностях исходов.

5. По числу критериев оценки альтернатив: а) простые, однокритериальные задачи, б) сложные, многокритериальные задачи. В задачах а) экономически приемлемо использование одного критерия оптимальности или удается специальными процедурами (например, «взвешиванием приоритетов») свести многокритериальный поиск к однокритериальному.

Сочетание признаков 1-5 позволяет группировать (классифицировать) в самом общем виде задачи и методы оптимального программирования, например: 1а) 2а) 3а) 4а) 5а) - задачи и методы линейного программирования, 1б) 2а) 3а) 4а) 5а) - задачи и методы нелинейного программирования, 1а) 2б) 3а) 4а) 5а) - задачи и методы целочисленного (дискретного) линейного программирования и т.д.