Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Давление под искривленной поверхностью жидкости. Капиллярные явления.Содержание книги
Поиск на нашем сайте
Если поверхность жидкости не плоская, а искривленная, то она оказывает на жидкость избыточное (добавочное) давление. Это давление, обусловленное силами поверхностного натяжения, для выпуклой поверхности положительно, а для вогнутой поверхности — отрицательно. Для расчета избыточного давления предположим, что свободная поверхность жидкости имеет форму сферы радиуса R, от которой мысленно отсечен шаровой сегмент, опирающийся на окружность радиуса r = R sin (рис. 100). На каждый бесконечно малый элемент длины l этого контура действует сила поверхностного натяжения F = l, касательная к поверхности сферы. Разложив F на два компонента (F1 и F2), видим, что геометрическая сумма сил F2 равна нулю, так как эти силы на противоположных сторонах контура направлены в обратные стороны и взаимно уравновешиваются. Поэтому равнодействующая сил поверхностного натяжения, действующих на вырезанный сегмент, направлена перпендикулярно плоскости сечения внутрь жидкости и равна алгебраической сумме составляющих F1: Разделив эту силу на площадь основания сегмента r 2, вычислим избыточное давление на жидкость, создаваемое силами поверхностного натяжения и обусловленное кривизной поверхности: Если поверхность жидкости вогнутая, то можно доказать, что результирующая сила поверхностного натяжения направлена из жидкости и равна Следовательно, давление внутри жидкости под вогнутой поверхностью меньше, чем в газе, на величину p.
Формулы (68.1) и (68.2) являются частным случаем формулы Лапласа, определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны: где R 1 и R 2 — радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости в дайной точке. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости.Для сферической искривленной поверхности (R 1 = R 2 = R) выражение (68.3) переходит в (68.1), для цилиндрической (R 1 = R и R 2 = ) — избыточное давление В случае плоской поверхности (R 1 = R 2 = ) силы поверхностного натяжения избыточного давления не создают. Капиллярность — это явление подъема или опускания жидкости в капиллярах. В достаточно широких сосудах короткоживущие силы притяжения между молекулами твердого тела и жидкости удерживают в виде мениска лишь незначительную часть жидкости в сосуде. основная поверхность — горизонтальная. В узких сосудах (капиллярах) масса жидкости невелика, поэтому различие между силой притяжения между молекулами жидкости и твердого тела и силой притяжения между молекулами жидкости приводит к капиллярности. Когда капилляр опущен в жидкость, то в случае смачивающей жидкости силы притяжения между молекулами жидкости и твердого тела Fж-т, то есть стенками капилляра, превосходят силы взаимодействия между молекулами жидкости Fж. Жидкость втягивается внутрь капилляра. Подъем жидкости в капилляре происходит до тех пор, пока результирующая сила Fв действующая на жидкость вверх, не уравновесится силой тяжести mg столба жидкости высотой h: Fв = mg. Жидкость, не смачивающая стенки капилляра, опускается в нем на расстояние h. Высота столба смачивающей жидкости в капилляре: h=2σρgRh=2σρgR ρρ- плотность жидкости. Чем меньше радиус капилляра, тем больше высота подъема жидкости в капилляре.
|
||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |


 (68.1)
(68.1)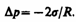 (68.2)
(68.2)
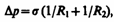 (68.3)
(68.3)