
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механическое движение. Скорость. УскорениеСодержание книги
Поиск на нашем сайте
Законы Ньютона. Первый закон Ньютона. Масса. Сила. Второй закон Ньютона. Третий закон Ньютона. Законы Ньютона – это обобщение большого количества эмпирических (опытных) данных. Они являются базой классической динамики и обычно рассматриваются совместно. I закон Ньютона: есливнешние силы отсутствуют или их действие на материальную точку скомпенсировано, то эта точка сохраняет состояние покоя равномерного прямолинейного движения до тех пор, пока внешнее воздействие не выведет ее из этого состояния. Свойство тел сохранять скорость называется инерцией. I закон Ньютона называется закон ом инерции. Он утверждает, что для поддержания равномерного движения не требуется внешних воздействий. Масса (m) – одна из основных характеристик материи, характеризует инертные свойства тел (m ин – инертная масса) и способность тел участвовать в тяготении (m гр – гравитационная масса). Их эквивалентность доказана в общей теории относительности (ОТО) Эйнштейна в четырехмерном пространстве (пространство-время). Различие появляется при переходе к обычному трехмерному пространству:
Для характеристики взаимодействия тел вводят понятие силы. Сила – это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело либо изменяет свою скорость (динамическое проявление силы), либо деформируется (статическое проявление силы). Единица измерения силы Второй закон Ньютона: "Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует". II закон Ньютона определяет характер изменения движения тела под действием внешней силы. Он утверждает, что если В системе СИ: II закон Ньютона – основной закон динамики поступательного движения. Его можно представить в виде: Третий закон Ньютона: ”Действию всегда есть равное и противоположное противодействие, иначе взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны”:
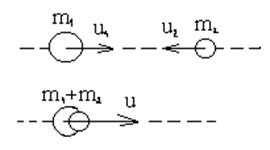
Соударение тел. Удар (или соударение)- это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения, называется линией удара. Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс. Абсолютно упругий удар - столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии. Обозначим скорости шаров массами m1 и m2 до удара через
При прямом центральном ударе векторы скоростей шаров до и после удара лежат на прямой линии, соединяющей их центры. Проекции векторов скорости на эту линию равны модулям скоростей. (Пояснение к рисунку выше) Их направления учтем знаками: положительное значение припишем движению вправо, отрицательное - движению влево. При указанных допущениях законы сохранения имеют вид. Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.
Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина (глины), движущихся навстречу друг другу. Если массы шаров m1 и m2, их скорости до удара Абсолютно неупругий удар – пример того, как происходит "потеря" механической энергии под действием диссипативных сил. Таблица 1.1
Закон сохранения момента импульса. Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси. Значение момента импульса Lz не зависит от положения точки 0 на оси z. При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдельная точка тела движется по окружности постоянного радиуса ri с некоторой скоростью vi. Скорость vi и импульс mivi перпендикулярны этому радиусу, т.е. радиус является плечом вектора mivi. Поэтому можно записать, что момент импульса отдельной точки относительно оси z равен: Liz=miviri. Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его точек:
Учитывая связь между линейно и угловой скоростями (vi=ωri), получим следующее выражение для момента импульса тела относительно неподвижной оси: Космические скорости. Первая космическая (круговая) скорость — минимальная скорость, которую надо сообщить телу, чтобы оно могло двигаться вокруг Земли по круговой орбите, т.е. превратиться в искусственный спутник Земли. По 2 закону Ньютона: Отсюда следует: Вторая космическая (параболическая) скорость — наименьшая скорость, которую надо сообщить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спутник Солнца, т. е. чтобы его орбита в поле тяготения Земли стала параболической. В этом случае кинетическая энергия тела должна быть равна работе, совершаемой против сил тяготения:
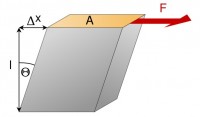
Третья космическая скорость — минимальная скорость, которую необходимо сообщить телу на Земле, чтобы оно покинуло пределы Солнечной системы, преодолев притяжение Солнца: v3 = 16,7 км/с. Деформации твердого тела. Под воздействием внешних сил твёрдые тела меняют свою форму и объем, т.е. деформируются. В результате действия приложенных к телу сил частицы, из которых оно состоит, перемещаются. Изменяются расстояния между атомами, их взаимное расположение. Это явление называют деформацией. Если после прекращения действия силы тело возвращает свою первоначальную форму и объём, то такая деформация называется упругой, или обратимой. В этом случае атомы снова занимают положение, в котором они находились до того, как на тело начала действовать сила. Если же в результате действия силы атомы смещаются от положений равновесия на такие расстояния, что межатомные связи на них уже не действуют, они не могут вернуться в первоначальное состояние и занимают новые положения равновесия. В этом случае в физическом теле происходят необратимые изменения. Такую деформацию называют пластичной, или необратимой. Под воздействием одной и той же силы тело может испытывать упругую деформацию, если сила приложена к нему на короткое время. Но если эта же сила будет воздействовать на это же тело длительно, то деформация может стать необратимой. Величина механического напряжения, при которой деформация тела всё ещё будет упругой, а само тело восстановит свою форму после снятия нагрузки, называется пределом упругости. При значениях выше этого предела тело начнёт разрушаться. Но разрушить твёрдое тело не так-то просто. Оно сопротивляется. И это его свойство называется прочностью. Типы деформации В зависимости от того, как приложена внешняя сила, различают деформации растяжения-сжатия, сдвига, изгиба, кручения.
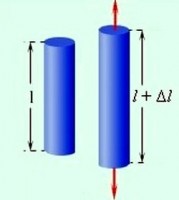
Деформация растяжения-сжатия
Деформация растяжения-сжатия вызывается силами, которые приложены к концам бруса параллельно его продольной оси и направлены в разные стороны. Под действием внешних сил частицы твёрдого вещества, колеблющиеся относительно своего положения равновесия, смещаются. Но этому процессу пытаются помешать внутренние силы взаимодействия между частицами, старающиеся удержать их в исходном положении на определённом расстоянии друг от друга. Силы, препятствующие деформации, называются силами упругости. Деформация сдвига
Если приложить внешнюю силу по касательной к поверхности бруска, нижняя часть которого закреплена, то возникает деформация сдвига. В этом случае параллельные слои тела как бы сдвигаются относительно друг друга. Деформация изгиба
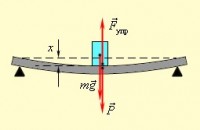
Такая деформация возникает, если концы бруса или стержня лежат на двух опорах. В этом случае на него действуют нагрузки, перпендикулярные его продольной оси. Деформация кручения
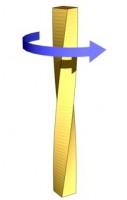
Кручение возникает в теле, если приложить пару сил к его поперечному сечению. В этом случае поперечные сечения будут поворачиваться вокруг оси тела и относительно друг друга. Второе начало термодинамики Второе начало термодинамики - один из основных законов термодинамики, устанавливающий необратимость макроскопических процессов, протекающих с конечной скоростью. Исторически второе начало термодинамики возникло из анализа работы тепловых Описание цикла Карно
Цикл Карно в координатах T—S Пусть тепловая машина состоит из нагревателя с температурой Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах T (температура) и S (энтропия). 1. Изотермическое расширение (на рис. 1 — процесс A→Б). В начале процесса рабочее тело имеет температуру 2. Адиабатическое расширение (на рис. 1 — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника
3. Изотермическое сжатие (на рис. 1 — процесс В→Г). Рабочее тело, имеющее температуру 4. Адиабатическое сжатие (на рис. 1 — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной. Кпд тепловой машины Карно Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику
Отсюда коэффициент полезного действия тепловой машины Карно равен
Поверхностное натяжение.
действия. Внутри жидкости на молекулу А действуют другие молекулы, при этом силы их действия скомпенсированы. Для молекулы В на поверхности жидкости равнодействующая этих сил отлична от нуля и направлена внутрь жидкости, т. к. в газе над поверхностью жидкости концентрация молекул намного меньше, чем в жидкости. Поэтому результирующие силы всех молекул поверхностного слоя оказывают на жидкость давление, называемое молекулярным, или внутренним. Это давление обусловлено только взаимодействием молекул жидкости и не действует на помещенное в жидкость тело.
Для перехода молекулы из глубины жидкости в поверхностный слой необходимо совершить работу против сил, действующих в нем; эта работа совершается молекулой за счет убывания кинетической энергии. Поэтому поверхностный слой обладает дополнительной потенциальной энергией, носящей название поверхностной энергии: Δ E =σΔ S, где σ — поверхностное натяжение (плотность поверхностной энергии). Состояние устойчивого равновесия характеризуется минимумом потенциальной энергии. Поэтому жидкость стремится сократить площадь свободной поверхности. Если при этом ограничивающий жидкость контур смещается на Δx внутрь жидкости, то силы поверхностного натяжения за счет убывания поверхностной энергии совершают работу
Δ A =Δ E = F Δ x = f ΔℓΔ x, где Δℓ — участок длины контура, а ΔℓΔx = ΔS — изменение площади поверхностного слоя. Из сопоставления выражений для ΔE и ΔA видно, что σ=f, т. е. поверхностное натяжение равно силе поверхностного натяжения на единицу длины контура, ограничивающего поверхность. Единица поверхностного натяжения в системе СИ — ньютон на метр (Н/м) или джоуль на квадратный метр (Дж/м2). С повышением температуры поверхностное натяжение уменьшается за счет увеличения среднего расстояния между молекулами. Поверхностное натяжение сильно зависит от примесей в жидкости. Поверхностно-активные вещества (ПАВ) — вещества, уменьшающие поверхностное натяжение. Например, мыло снижает поверхностное натяжение воды с ~7.5·10-2 Н/м до ~4.5·10-2 Н/м. Другие вещества, напротив, увеличивают поверхностное натяжение за счет того, что их молекулы взаимодействуют с молекулами жидкости сильнее, чем молекулы жидкости между собой. Например, поваренная соль увеличивает поверхностное натяжение воды. Смачивание. Если граничат друг с другом сразу три среды — твердая, жидкая и газообразная — то система принимает конфигурацию с минимальной суммарной потенциальной энергией (поверхностной, в поле тяготения и т. д.). Контур, по которому граничат три среды, располагается на поверхности твердого тела так, что сумма проекций всех сил, приложенных к каждому элементу Δℓ контура, на касательную к поверхности твердого тела равна нулю. При этом условие равновесия элемента Δℓ контура имеет вид: σтгΔℓ=σтж Δℓ+σжгΔℓcosθ.
По этому выражению краевой угол определяется только в тех случаях, когда
Данное неравенство не выполняется в 2 случаях: 1) σтг>σтж+σжг : как бы ни был мал краевой угол, сила поверхностного натяжения на границе твердое тело — газ перекомпенсирует остальные силы, и жидкость неограниченно растекается по поверхности твердого тела; при этом имеет место полное смачивание, краевой угол равен нулю; 2) σтж>σтг+σжг : как бы ни был краевой угол близок к 180°, сила поверхностного натяжения на границе твердое тело — жидкость перекомпенсирует остальные, и поверхность раздела жидкой и твердой сред стягивается в точку; при этом имеет место полное несмачивание, краевой угол равен 180°. При соблюдении условия Смачивание и несмачивание относительны, т. к. жидкость, смачивающая одну твердую поверхность, не смачивает другую. Например, вода смачивает стекло, но не смачивает парафин. Несмачивание приводит к удержанию на поверхности жидкости твердых тел с плотностью больше, чем у жидкости (например, удержание на поверхности воды смазанной жиром иголки, «плавание» печатной платы на поверхности травильного раствора H2O+CuSO4+NaCl). Смачивание применяется в технике, например, при флотационном отделении руды от пустой породы: измельченную руду взбалтывают в жидкости, смачивающей пустую породу и не смачивающей минерал, и продувают воздух через эту смесь. При этом пустая порода тонет, а минерал всплывает и удерживается на поверхности жидкости силами поверхностного натяжения. Также при механической обработке металлов их смачивают специальными жидкостями. Механическое движение. Скорость. Ускорение Механическое движение – это взаимные изменения положения тел друг относительно друга или взаимного расположения частей тела. Любому описанию механического движения тела должен предшествовать выбор системы отсчета (СО). Она состоит из какого-либо неподвижного твердого тела (отсчета) и связанной с ним системы координат, в которой указывается начало отсчета времени. В механике чаще всего используется координатная форма описания движения: положение материальной точки задается ее радиус-вектором. Это уравнение эквивалентно трем скалярным: x=x(t); y=y(t); z=z(t).
Вектор Для характеристики движения тела вводится векторная величина – скорость Если тело проходит за время Δ t путь Δ s, модуль которого равен Δ r (при условии малости промежутка Δ t), скорость определяется как Движение, при котором скорость постоянна, называется равномерным. В случае неравномерного движения важно знать, как изменяется скорость с течением времени, по модулю (величине) Среднее ускорение Как и скорость, ускорение можно в любой момент времени представить в виде двух составляющих
Нормальная составляющая: где R – радиус кривизны траектории в данной точке. В зависимости от значений 1. 2.
Следует помнить о различии в общем случае изменения пути и координат(ы): не всегда 3. В общем случае:
|
|||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.108.107 (0.014 с.) |

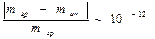 .
.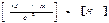 (ньютон).
(ньютон).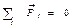 , то
, то 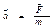 , где
, где 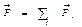 – равнодействующая всех сил.
– равнодействующая всех сил.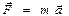 .
.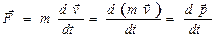 , так как в ньютоновской (классической) механике т<< c (с – скорость света в вакууме), т.е.
, так как в ньютоновской (классической) механике т<< c (с – скорость света в вакууме), т.е. 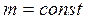 . Величина
. Величина 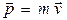 называется импульсом (количеством движения) тела.
называется импульсом (количеством движения) тела.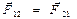 .
.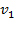 и
и 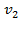 , после удара - через
, после удара - через 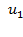 и
и 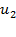 .
.
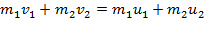
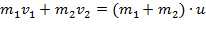

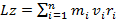
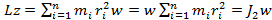 , (1) т.е. момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость. Продифференцировав выражение по времени, получим:
, (1) т.е. момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость. Продифференцировав выражение по времени, получим: 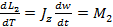 Это еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всех внешних сил, действующих на тело.
Это еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всех внешних сил, действующих на тело.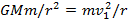 ;
;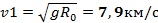
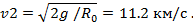

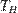 , холодильника с температурой
, холодильника с температурой 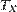 и рабочего тела.
и рабочего тела.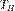 , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты
, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты 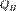 . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.
. При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.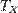 , тело совершает механическую работу, а энтропия остаётся постоянной.
, тело совершает механическую работу, а энтропия остаётся постоянной.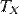 , приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты
, приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты 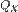 . Над телом совершается работа, его энтропия уменьшается.
. Над телом совершается работа, его энтропия уменьшается.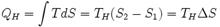 .
.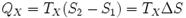 .
.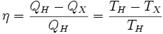 .
. На каждую молекулу жидкости со стороны окружающих молекул действуют силы притяжения, быстро убывающие с расстоянием; начиная с некоторого минимального расстояния (~ 10-9 м) данными силами можно пренебречь. Это расстояние называется радиусом молекулярного действия r, а сфера радиуса r — сферой молекулярного
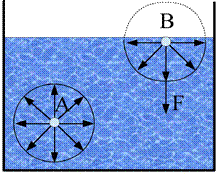
На каждую молекулу жидкости со стороны окружающих молекул действуют силы притяжения, быстро убывающие с расстоянием; начиная с некоторого минимального расстояния (~ 10-9 м) данными силами можно пренебречь. Это расстояние называется радиусом молекулярного действия r, а сфера радиуса r — сферой молекулярного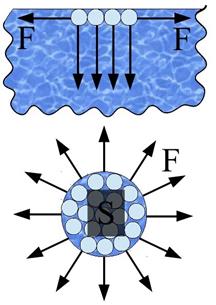 На молекулы поверхностного слоя также действуют силы F, которые лежат в плоскости, касательной к поверхности жидкости. Для всех молекул внутри площадки S эти силы скомпенсированы, а для молекул вдоль контура площадки равнодействующие этих сил отличны от нуля, направлены наружу нормально к контуру и касательны к поверхности жидкости. Эти силы называются силами поверхностного натяжения.
На молекулы поверхностного слоя также действуют силы F, которые лежат в плоскости, касательной к поверхности жидкости. Для всех молекул внутри площадки S эти силы скомпенсированы, а для молекул вдоль контура площадки равнодействующие этих сил отличны от нуля, направлены наружу нормально к контуру и касательны к поверхности жидкости. Эти силы называются силами поверхностного натяжения.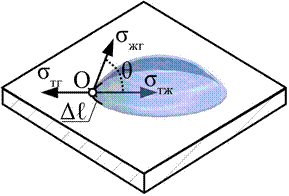 Угол θ внутри жидкости между касательными к поверхностям твердого тела и жидкости называется краевым углом. Из условия равновесия контура жидкости имеем:
Угол θ внутри жидкости между касательными к поверхностям твердого тела и жидкости называется краевым углом. Из условия равновесия контура жидкости имеем: 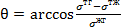
 ≤1
≤1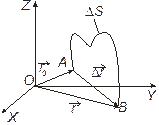 Рассмотрим (рис. 1.1) движение материальной точки вдоль произвольной траектории. Отсчет времени начинают с момента, соответствующего точке А. Длина участка АB, пройденного телом с начала отсчета времени, называется длиной пути Δ s и является скалярной функцией времени.
Рассмотрим (рис. 1.1) движение материальной точки вдоль произвольной траектории. Отсчет времени начинают с момента, соответствующего точке А. Длина участка АB, пройденного телом с начала отсчета времени, называется длиной пути Δ s и является скалярной функцией времени. называется перемещением тела. В случае прямолинейного движения
называется перемещением тела. В случае прямолинейного движения 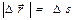 . Сказанное справедливо для движения в одном направлении, а в общем случае
. Сказанное справедливо для движения в одном направлении, а в общем случае 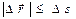 .
.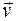 , которая определяет быстроту движения и его направление в данный момент времени t.
, которая определяет быстроту движения и его направление в данный момент времени t.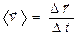 - средняя скорость (м/c);
- средняя скорость (м/c); 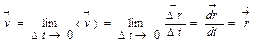 – мгновенная скорость (всегда направлена по касательной в данной точке траектории). Траектория – это линия, которую описывает тело при движении в пространстве. Если траектория лежит в одной плоскости, движение называется плоским или двумерным (движение тела, брошенного под углом к горизонту, движение заряженной частицы в магнитном поле, когда скорость перпендикулярна вектору магнитной индукции
– мгновенная скорость (всегда направлена по касательной в данной точке траектории). Траектория – это линия, которую описывает тело при движении в пространстве. Если траектория лежит в одной плоскости, движение называется плоским или двумерным (движение тела, брошенного под углом к горизонту, движение заряженной частицы в магнитном поле, когда скорость перпендикулярна вектору магнитной индукции  .
. и направлению
и направлению  (последний интеграл будет иметь другой вид). Для этого вводят векторную величину – ускорение
(последний интеграл будет иметь другой вид). Для этого вводят векторную величину – ускорение 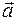 .
.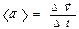 (м/c2), а мгновенное
(м/c2), а мгновенное 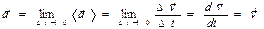 .
.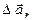 (
(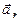 – тангенциальной) и
– тангенциальной) и 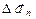 (
(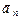 – нормальной): по теореме Пифагора
– нормальной): по теореме Пифагора 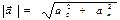 , так как
, так как 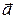 ^
^ 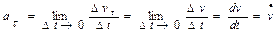 .
.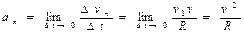 ,
, 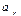 и
и 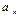 , можно выделить следующие типы движения:
, можно выделить следующие типы движения: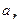 =0,
=0, 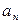 =0 – равномерное движение;
=0 – равномерное движение;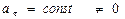 ,
, 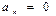 – равнопеременное прямолинейное движение; при этом
– равнопеременное прямолинейное движение; при этом 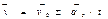 , тогда
, тогда 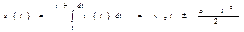 .
. 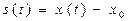 .
.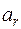 =0,
=0, 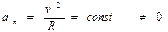 – равномерное вращение по окружности, так как R = const.
– равномерное вращение по окружности, так как R = const.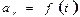 и
и 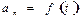 .
.


