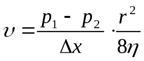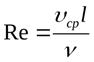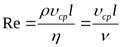Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание движения жидкостей. Уравнение Бернулли и следствия из него.Содержание книги
Поиск на нашем сайте
Движение жидкостей называется течением. Совокупность частиц движущейся жидкости называется потоком. Линия тока - это линия, проведенная так, что касательная к ней совпадает по направлению с вектором скорости жидкости в соответствующих точках пространства. Часть жидкости, ограниченная линиями тока, называется трубкой тока.
Рассмотрим несжимаемую жидкость: sv = const физический смысл произведения sv -объем жидкости, проходящей через сечение s за 1 с. Вопрос 36: Ур-ние Бернулли и следствия из него. Давление в жидкости и газе. Идеальная жидкость - это жидкость, в которой отсутствуют силы внутреннего трения. Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения. В момент времени t жидкость заполняла участок ограниченный S1 и S2,
По закону сохранения энергии:
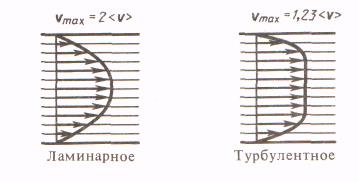
ур-ние Бернулли. Уравнение Бернулли есть выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Величину р называют статистическим давлением, величину Для горизонтальной трубки тока уравнение Бернулли имеет вид rv2/2 + p = const, где величина rv2/2 + p называется полным давлением. Из последнего уравнения и уравнения неразрывности следует, что при течение жидкости по горизонтальной трубке, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах. Если жидкость неподвижна v=0, то p1 и p2=const и полное давление определяется гидростатическим и статическим давлением. 15. Вязкость (внутреннее трение). Ламинарный и турбулентный режимы течения жидкостей. Вязкость или внутреннее трение – свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Это явлениеопределяет диссипацию (поглощение) энергии при деформации среды. При деформации сдвига вязкость называют сдвиговой, при деформации объема (всестороннее сжатие) проявляется объемная вязкость. В данном случае мы будем касаться только вопроса сдвиговой вязкости. Суть явления состоит в том, что движущиеся слои газа или жидкости увлекают соседние слои и, наоборот, неподвижные (или движущиеся с меньшей скоростью) тормозят более быстрые соседние слои. Таким образом, между любыми соседними слоями рассматриваемой среды действуют силы внутреннего трения (или силы вязкости). Механизм возникновения этих сил заключается в переносе импульса (количества движения) от одного слоя к другому. Совместно с теплопроводностью и диффузией вязкость относят к явлениям переноса (теплопроводность связана с переносом частицами среды тепловой формы передачи энергии, диффузия – с переносом массы). Существуют две различные формы, два режима течения жидкостей: ламинарное и турбулентное течения. Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа). Ламинарное течение жидкости наблюдается при небольших скоростях ее движения. При ламинарном течении траектории всех частиц параллельны и формой своей повторяют границы потока. В круглой трубе, например, жидкость движется цилиндрическими слоями, образующие которых параллельны стенкам и оси трубы. В прямоугольном, бесконечной ширины канале жидкость движется как бы слоями, параллельными его дну. В каждой точке потока скорость остается по направлению постоянной. Если скорость при этом не меняется со временем и по величине, движение называется установившимся. Для ламинарного движения в трубе эпюра распределения скорости в поперечном сечении имеет вид параболы с максимальной скоростью на оси трубы и с нулевым значением у стенок, где образуется прилипший слой жидкости. Внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным. Скорости последующих слоев тем больше, чем больше их расстояние до поверхности трубы, и наибольшей скоростью обладает слой, движущийся вдоль оси трубы. Профиль усредненной скорости турбулентного течения в трубах (рис. 53) отличается от параболического профиля соответствующего ламинарного течения более быстрым возрастанием скорости υ. Среднее значение скорости в поперечном сечении круглой трубы при установившемся ламинарном течении определяется законом Гагена — Пуазейля:
где р1 и р2 — давление в двух поперечных сечениях трубы, отстоящих друг от друга на расстоянии Δх; r — радиус трубы; η — коэффициент вязкости. Закон Гагена — Пуазейля легко может быть проверен. При этом оказывается, что для обычных жидкостей он справедлив лишь при малых скоростях течения или малых размерах труб. Точнее сказать, закон Гагена—Пуазейля выполняется лишь при малых значениях числа Рейнольдса:
где υ — средняя скорость в поперечном сечении трубы; l — характерный размер, в данном случае — диаметр трубы; ν — коэффициент кинематической вязкости. Английский ученый Осборн Рейнольдс (1842 — 1912) в 1883 г. произвел опыт по следующей схеме: у входа в трубу, по которой течет установившийся поток жидкости, помещалась тонкая трубка так, чтобы ее отверстие находилось на оси трубки. Через трубочку в поток жидкости подавалась краска. Пока существовало ламинарное течение, краска двигалась примерно вдоль оси трубы в виде тонкой, резко ограниченной полоски. Затем, начиная с некоторого значения скорости, которое Рейнольдс назвал критическим, на полоске возникли волнообразные возмущения и отдельные быстро затухающие вихри. По мере роста скорости число их становилось больше, и они начинали развиваться. При некотором значении скорости полоска распадалась на отдельные вихри, которые распространялись на всю толщину потока жидкости, вызывая интенсивное перемешивание и окрашивание всей жидкости. Такое течение было названо турбулентным.
Начиная с критического значения скорости, нарушался и закон Гагена — Пуазейля. Повторяя опыты с трубами разного диаметра, с разными жидкостями, Рейнольдс обнаружил, что критическая скорость, при которой нарушается параллельность векторов скоростей течения, менялась в зависимости от размеров потока и вязкости жидкости, но всегда таким образом, что безразмерное число принимало в области перехода от ламинарного течения к турбулентному определенное постоянное значение. Английский ученый О. Рейнольдс (1842 — 1912) доказал, что характер течения зависит от безразмерной величины, называемой числом Рейнольдса:
Турбулентное течение жидкостей наиболее распространено в природе и технике. Течение воздуха в. атмосфере, воды в морях и реках, в каналах, в трубах всегда турбулентно. В природе ламинарное движение встречается при фильтрации воды в тонких порах мелкозернистых грунтов.
|
||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.234.182 (0.011 с.) |


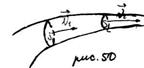 Течение жидкости называют стационарным (установившимся), если форма и расположение линий тока, а также скорости в каждой точке жидкости, со временем не изменяются.
Течение жидкости называют стационарным (установившимся), если форма и расположение линий тока, а также скорости в каждой точке жидкости, со временем не изменяются.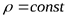 ,s1v1 = s2v2. Это соотношение справедливо для любых сечений трубки, следовательно,
,s1v1 = s2v2. Это соотношение справедливо для любых сечений трубки, следовательно,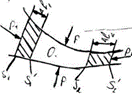 а в момент времени
а в момент времени  , она занимает объём
, она занимает объём 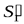 и
и  . В силу неразрывности струи заштрихованные объёмы будут иметь одинаковую величину.
. В силу неразрывности струи заштрихованные объёмы будут иметь одинаковую величину.
 ;
;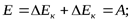

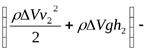
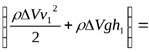
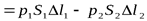
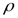 v12/2 +
v12/2 + 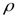 gh1 + p1 =
gh1 + p1 = 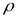 v2/2 называют динамическим давлением, а величина
v2/2 называют динамическим давлением, а величина