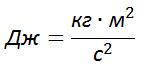Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика твердого тела, вращающегося вокруг неподвижной оси. Кинетическая энергия вращательного движения.Содержание книги
Поиск на нашем сайте
Описанное нами движение твердого тела относительно неподвижной точки является основным видом движения. Однако вычислить вектор
Обозначим Ii – момент инерции точки находящейся на расстоянии R от оси вращения
Момент инерции тела служит мерой инертности во вращательном движении. Как видно, момент инерции I – величина скалярная.
(Сравним: Это основное уравнение динамики тела, вращающегося вокруг неподвижной оси. (Сравним:
(Сравним: – кинетическая энергия движущегося тела, – его масса, – скорость его движения. Условное обозначение — Единица измерения энергии — Дж (джоуль).
Кинетическая энергия характеризует движение тела. Это векторная физическая величина. Она равна нулю, когда тело неподвижно. Кинетическую энергию подразделяют на энергию поступательного и вращательного движения. Указанная формула имеет смысл только для поступательного движения
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 112; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.237.153 (0.009 с.) |

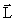 – момент импульса системы относительно произвольной точки – не просто: надо знать шесть проекций (три задают положение тела, три задают положение точки).
– момент импульса системы относительно произвольной точки – не просто: надо знать шесть проекций (три задают положение тела, три задают положение точки). 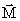 – момента внешних сил, направленные вдоль x и y, компенсируются моментами сил реакции закрепления. Вращение вокруг оси z происходит только под действием о проще найти момент импульса
– момента внешних сил, направленные вдоль x и y, компенсируются моментами сил реакции закрепления. Вращение вокруг оси z происходит только под действием о проще найти момент импульса  у всех точек разная, введем вектор угловой скорости
у всех точек разная, введем вектор угловой скорости  , причем
, причем 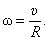 . Тогда
. Тогда  .
. 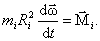
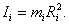
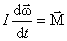 или Это основное уравнение динамики тела, вращающегося вокруг неподвижной оси. (Сравним:
или Это основное уравнение динамики тела, вращающегося вокруг неподвижной оси. (Сравним:  – основное уравнение динамики поступательного движения тела).
– основное уравнение динамики поступательного движения тела).  ,
, 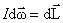 ,
, 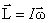 .
.
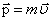 – для поступательного движения).
– для поступательного движения).