Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса и их анализ.Содержание книги
Поиск на нашем сайте
Уравнение состояния идеального газа выводилось в предположении отсутствия сил притяжения между молекулами при r>r0 и бесконечно больших модулей сил отталкивания при r<r0. Для реального же газа при больших плотностях необходимо учитывать силы притяжения между молекулами, а также конечный размер самих молекул. Уравнение состояния реального газа вывел голландский физик И. Ван-дер-Ваальс, введя в уравнение Клапейрона — Менделеева две поправки. 1. Учет собственного объема молекул. Наличие сил отталкивания сводится к тому, что свободный объем, в котором молекулы могут двигаться, равен V-b, где b — объем, занимаемый самими молекулами. Две молекулы не могут сблизиться на расстояние меньше эффективного диаметра d молекулы, поэтому для центров обеих молекул недоступен объем сферы радиуса d, равный восьми объемам молекулы, или учетверенный объем молекулы в расчете на одну молекулу. Поэтому поправка b равна учетверенному собственному объему молекул. 2. Учет притяжения молекул. Действие сил притяжения между молекулами приводит к появлению внутреннего давления в газе. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема. Вводя эти поправки в уравнение Клапейрона — Менделеева, получим уравнение состояния реального газа (уравнение Ван-дер-Ваальса) для одного моля газа:
Для произвольной массы газа: Поправки a и b — постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно a и b). Уравнение Ван-дер-Ваальса было выведено с принятием ряда упрощений и поэтому является приближенным. Существуют и другие уравнения, некоторые из них более точно описывают состояния реальных газов; однако все они более сложны. Изотермы Ван-дер-Ваальса и их анализ.
Раскрыв скобки в уравнении Ван-дер-Ваальса для одного моля газа и умножив выражение на Vm2, получим кубическое уравнение относительно Vm:
Кубическое уравнение со свободным членом имеет хотя бы один вещественный корень, остальные корни могут как быть вещественными, так и комплексными. Последние не имеют физического смысла, т. к. объем может быть только вещественным. Уравнению с тремя вещественными корнями (
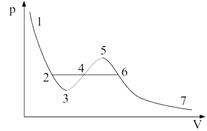
При T < Tкр на изотерме имеется участок (3-5), в котором при увеличении объема увеличивается и давление. Практика же показывает, что в природе такие состояния не реализуются. Наличие участка 3-5 означает, что при постепенном изменении объема вещество в некоторый момент распадается на две фазы. Истинная — экспериментальная — изотерма (изотерма Эндрюса) имеет вид ломаной 7-6-2-1; участок 7-6 соответствует газообразному состоянию, участок 2-1 — жидкому. На участке 6-2 наблюдается динамическое равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при T<Tкр называется паром; пар, находящийся в равновесии со своей жидкостью, называется насыщенным.
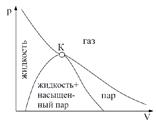
Линия, проходящая через крайние точки горизонтальных участков семейства изотерм Эндрюса, имеет вид куполообразной кривой и вместе с критической изотермой делит область под ней на три участка: слева от точки К — жидкость, под «куполом» — область двухфазных состояний, справа — пар. Пар при изотермическом сжатии сжижается. Газ при T>Tкр не может быть сжижен ни при каком давлении. При некоторых условиях на практике могут быть реализованы состояния на участках 2-3 и 5-6 изотермы Ван-дер-Ваальса. Данные неустойчивые состояния называются метастабильными. Участок 2-3 изображает перегретую жидкость, участок 5-6 — пересыщенный пар. При достаточно низких температурах изотерма пересекает ось V, переходя в область отрицательных давлений. Вещество при отрицательном давлении находится в состоянии растяжения (растянутая жидкость), такие состояния при определенных условиях также реализуются.
|
||||
|
Последнее изменение этой страницы: 2021-06-14; просмотров: 166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.254.25 (0.007 с.) |

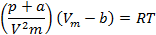
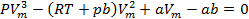
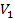 ,
, 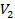 ,
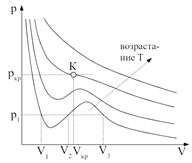
, 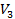 ) соответствуют изотермы при низких температурах и давлениях. При повышении температуры различия между
) соответствуют изотермы при низких температурах и давлениях. При повышении температуры различия между 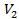 ,
, 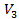 уменьшаются, и при некоторой критической температуре, своей для каждого вещества, при любом давлении остается только одно значение объема — Vкр в точке К — являющееся корнем уравнения Ван-дер-Ваальса; касательная к изотерме в этой точке параллельна оси V. Точка К и соответствующие ей параметры состояния называются критическими.
уменьшаются, и при некоторой критической температуре, своей для каждого вещества, при любом давлении остается только одно значение объема — Vкр в точке К — являющееся корнем уравнения Ван-дер-Ваальса; касательная к изотерме в этой точке параллельна оси V. Точка К и соответствующие ей параметры состояния называются критическими.