
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение и характеристики дискретной случайной величиныСодержание книги
Поиск на нашем сайте
Для того чтобы полностью охарактеризовать дискретную случайную величину, надо указать все ее возможные значения и соответствующие им вероятности. Совокупность этих данных называется законом распределения дискретной случайной величины. Закон распределения можно задать в виде таблицы, графика (рис. 5.1) или формулы.
Поскольку все возможные значения дискретной случайной величины представляют полную систему, то сумма их вероятностей должна быть равна единице:
Важным примером распределения дискретной случайной величины является так называемое биноминальное распределение. Оно позволяет определить вероятность того, что событие A произойдет m раз в n испытаниях:
где p - вероятность наступления события A в каждом отдельном испытании, Пример 1. Появление колонии микроорганизмов данного вида в определенных условиях оценивается с вероятностью 0,7. Найти вероятность того, что в 6 пробах колония появится 4 раза. Решение
Закон распределения можно задать и с помощью функции распределения. Функцией распределения
где x – произвольное вещественное число. Функция распределения дискретной случайной величины определяется по формуле:
Пример 2. Построить функцию распределения дискретной случайной величины X, если задан закон распределения:
Решение Событие Событие Событие тогда Событие тогда В результате искомая функция распределения задается следующим образом:
График данной функции показан на рис. 5.2.
Случайную величину характеризуют такими числовыми параметрами, как математическое ожидание, дисперсия и среднее квадратичное отклонение. Математическим ожиданием
Математическое ожидание указывает некоторое значение, вокруг которого группируются все значения случайной величины. Дисперсией
Для дискретной случайной величины дисперсию вычисляют по формуле:
Дисперсия характеризует степень рассеяния или разброса отдельных значений случайной величины около математического ожидания. Средним квадратичным отклонением
Данный параметр удобен тем, что он имеет размерность самой случайной величины.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 162; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.125.236 (0.005 с.) |


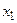
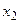
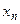
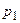
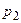
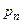
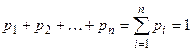 (условие нормировки).
(условие нормировки).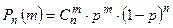 (формула Бернулли),
(формула Бернулли),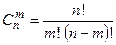 - число сочетаний из n элементов по m.
- число сочетаний из n элементов по m.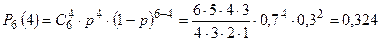 .
.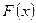 случайной величины X называется вероятность того, что величина X примет значение, меньше данного:
случайной величины X называется вероятность того, что величина X примет значение, меньше данного: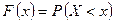 ,
,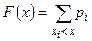 .
.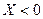 является невозможным, следовательно, в этом интервале
является невозможным, следовательно, в этом интервале 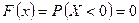 ;
;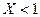 равносильно
равносильно 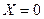 , тогда
, тогда 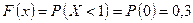 ;
;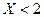 равносильно
равносильно 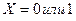 ,
,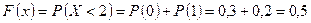 ,
,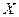 меньше любого числа большего 2 равносильно
меньше любого числа большего 2 равносильно 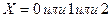 ,
,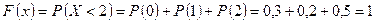 .
.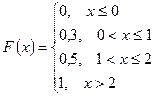 .
.
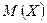 дискретной случайной величины X называется сумма произведений всех ее возможных значений на их вероятности:
дискретной случайной величины X называется сумма произведений всех ее возможных значений на их вероятности: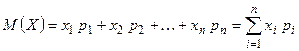 .
.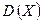 называют математическое ожидание квадрата отклонения возможных значений случайной величины X от своего математического ожидания:
называют математическое ожидание квадрата отклонения возможных значений случайной величины X от своего математического ожидания: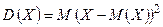 .
.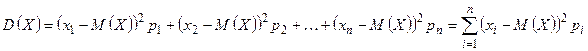 .
.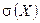 случайной величины X называется корень квадратный из дисперсии:
случайной величины X называется корень квадратный из дисперсии: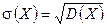 .
.


