
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи для решения по высшей математикеСодержание книги
Поиск на нашем сайте
Элементы дифференциального исчисления Функция Постройте графики следующих функций: 1.1. 1.2. 1.3. Предел функции Найдите пределы:
Производная элементарных функций 1.6. Запишите таблицу производных элементарных функций. Правила дифференцирования Используя правила дифференцирования, найдите производные следующих функций:
Производная сложной функции Найдите производные следующих сложных функций:
Дифференциал функции Найдите дифференциалы следующих функций:
Производные высших порядков Проведите повторное дифференцирование следующих функций: 1.35. 1.36. 1.37.
Элементы интегрального исчисления
Неопределенный интеграл Найдите следующие неопределенные интегралы:
Метод замены переменных Воспользуйтесь методом замены переменных для нахождения следующих неопределенных интегралов:
Метод интегрирования по частям Воспользуйтесь методом интегрирования по частям для нахождения следующих неопределенных интегралов:
Определенный интеграл Вычислите следующие определенные интегралы:
Обыкновенные дифференциальные уравнения первого порядка
Основные понятия и определения теории дифференциальных уравнений 3.1. Докажите, что любая функция вида 3.2. Найдите частное решение предыдущего уравнения при условии, что 3.3. Решите предыдущее уравнение методом разделяющихся переменных.
Общее решение дифференциальных уравнений Найдите общее решение следующих дифференциальных уравнений:
Частное решение дифференциальных уравнений Найдите частное решение следующих дифференциальных уравнений: 3.19. 3.20. 3.21.
Приложения дифференциальных уравнений первого порядка
3.23. Скорость, с которой лекарственный препарат расходуется в организме пациента, пропорциональна его массе. Найдите закон убывания массы препарата от времени, если пациенту однократно была сделана инъекция массой 3.24. Рассмотрите предыдущую задачу для случая, когда препарат вводился пациенту с постоянной скоростью q (сл. инфузии). Начальные условия выберите в следующем виде:
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.141.5 (0.011 с.) |

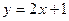 ;
;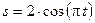 ;
;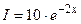 ;
;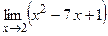 ;
;
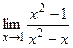 ;
;
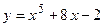 ;
1.8.
;
1.8. 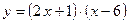 ;
1.9.
;
1.9.  ;
1.10.
;
1.10. 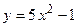 ;
1.11.
;
1.11. 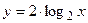 ;
1.12.
;
1.12. 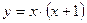 ;
1.13.
;
1.13. 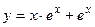 ;
1.14.
;
1.14. 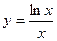 ;
1.15.
;
1.15. 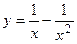 ;
1.16.
;
1.16. 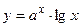 ;
;
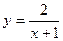 ;
1.18.
;
1.18. 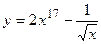 ;
1.19.
;
1.19. 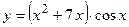 ;
1.20.
;
1.20. 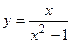 ;
1.21.
;
1.21. 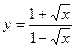 ;
1.22.
;
1.22. 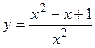 ;
1.23.
;
1.23. 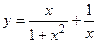 ;
;
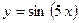 ;
1.25.
;
1.25. 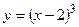 ;
1.26.
;
1.26. 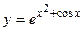 1.27.
1.27. 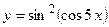
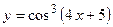 1.29.
1.29. 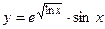 1.30.
1.30. 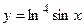
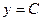 ;
1.32.
;
1.32. 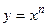 ;
;
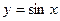 ;
1.34.
;
1.34. 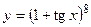 ;
;
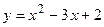 ,
, 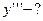
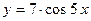 ,
, 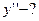
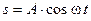 ,
, 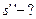
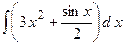 ;
2.2.
;
2.2. 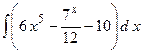 ;
2.3.
;
2.3. 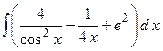 ;
2.4.
;
2.4. 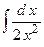 ;
2.5.
;
2.5. 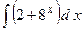 2.6.
2.6. 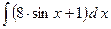 ;
;
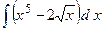 ;
2.8.
;
2.8. 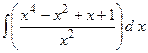 ;
2.9.
;
2.9. 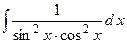 ;
2.10.
;
2.10. 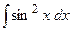 ;
2.11.
;
2.11. 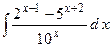 ;
;
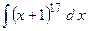 ;
2.13.
;
2.13. 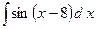 ;
2.14.
;
2.14. 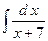 ;
;
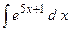 ;
2.16.
;
2.16. 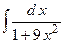 ;
2.17.
;
2.17. 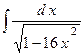 ;
;
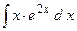 ;
2.19.
;
2.19. 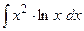 ;
;
 ;
2.21.
;
2.21. 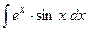 ;
;
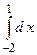 ;
2.23.
;
2.23. 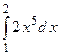 ;
2.24.
;
2.24. 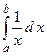 ;
2.25.
;
2.25. 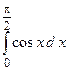 ;
2.26.
;
2.26. 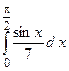 ;
2.27.
;
2.27. 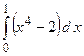 ;
;
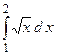 ;
2.29.
;
2.29. 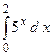 ;
2.30.
;
2.30. 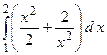 ;
2.31.
;
2.31. 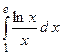 ;
2.32.
;
2.32. 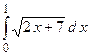 ;
2.33.
;
2.33. 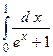 .
.
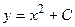 является общим решением дифференциального уравнения
является общим решением дифференциального уравнения 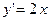 .
.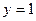 при
при 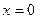 .
.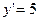 ;
3.5.
;
3.5. 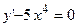 ;
3.6.
;
3.6. 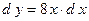 ;
3.7.
;
3.7. 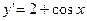 ;
3.8.
;
3.8. 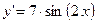 ;
3.9.
;
3.9. 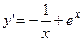 ;
3.10.
;
3.10. 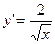 ;
3.11.
;
3.11. 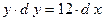 ;
;
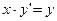 ;
3.13.
;
3.13. 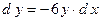 ;
3.14.
;
3.14. 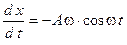 ;
3.15.
;
3.15. 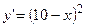 ;
3.16.
;
3.16. 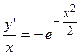 ;
3.17.
;
3.17. 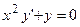 ;
3.18.
;
3.18. 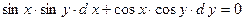 ;
;
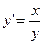 ,
, 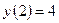 ;
;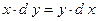 ,
, 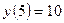 ;
;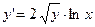 ,
, 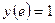 (интеграл
(интеграл 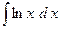 следует вычислять по частям);
следует вычислять по частям);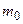 . Изобразите график уменьшения массы препарата в крови со временем.
. Изобразите график уменьшения массы препарата в крови со временем.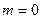 при
при 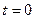 .
.


