
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Секция «нефтегазовое Дело, нефтепереработка, нефтехимия»Содержание книги
Поиск на нашем сайте
ОПТИМИЗАЦИЯ СИСТЕМЫ СБОРА И ПОДГОТОВКИ НЕФТИ Сазонов Н.А., научный руководитель доц. Алекина Е.В. (Самарский государственный технический университет)
Работа посвящена оптимизации системы сбора и подготовки скважинной продукции на месторождениях, путем подбора оптимального давления первой ступени сепарации и исследования влияния остаточного попутного нефтяного газа на реологические характеристики транспортируемой жидкости. В программно-вычислительном комплексе AspenHYSYS была смоделирована первая ступень сепарации, с последующей транспортировкой жидкой фазы в газонасыщенном состоянии под собственным давлением. В качестве объектов исследования были взяты исходные физико-химические характеристики нефти существенно отличающих по вязкостным характеристикам и близким по газовому фактору. Результаты расчета показали, что повышение давления на первой ступени сепарации приводит к увеличению количества растворенного попутного нефтяного газа в нефти, уменьшению вязкости, а значит улучшение транспортных характеристик нефти. В работе приведены экономические расчеты целесообразности транспорта нефти в газонасыщенном состоянии.
ОЦЕНКА ВЛИЯНИЯ ФАКТИЧЕСКОГО ЗАБОЙНОГО ДАВЛЕНИЯ Свиридова И.А., научный руководитель доц. Баландин Л.Н. (Самарский государственный технический университет)
Максимальная критическая депрессия ∆Ркр:
где Рзаб.кр – критическое забойное давление, дебит является максимальным. Дальнейшее снижение забойного давления ниже Рзаб.кр приводит к интенсивному выделению газа из нефти. Для вычисления критического забойного давления мы применили следующую зависимость:
где G'0 – газовый фактор продукции скважины, м3/т; Рпл – пластовое давление, МПа.
ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ФИНАНСОВЫХ ПОТОКОВ НЕФТЕДОБЫВАЮЩЕГО ПРЕДПРИЯТИЯ В МОДУЛЕ SIMULINK Трифонов А.Д., научный руководитель доц. Пономарев В.П. (Самарский государственный технический университет)
Создана интегрированная динамическая модель финансовых потоков нефтедобывающей компании. В модели выделены компьютерные подсистемы подготовки и эксплуатации месторождений, транспортировки и сбыта нефти нефтеперерабатывающим заводам, нефтепроводу за рубеж, речным и железнодорожным перевозкам, уплаты общегосударственных и региональных налогов, управления компанией, которые раскрываются и детально наполняются необходимыми блоками модуля SIMULINK. В подсистему управления компанией входит блок анализа мировых цен на нефть, таможенных пошлин, внешних указаний, которые во многом определяют выделение инвестиций ираспределение нефти между поставками на НПЗ и за рубеж. После ввода начальных условий включается процесс дискретного моделирования во времени (по месяцам) и выдаются графики изменения основных параметров.
Отличительной особенностью компьютерной модели является: – наглядность работы; – функциональная связь подсистем и блоков; – быстрота расчета различных вариантов; – визуализация результатов моделирования (в виде различных графиков по времени). Компьютерная модель позволяет дополнять её математическими блоками пакета MATLAB для выбора оптимальных вариантов управления компанией.
СЕКЦИЯ «ПРИКЛАДНАЯ МАТЕМАТИКА
ОПРЕДЕЛЕНИЕ ГАРМОНИЧЕСКОЙ ФУНКЦИИ СКОРОСТИ ЖИДКОСТИ ВНУТРИ КРУГОВОГО ЦИЛИНДРА, НАХОДЯЩЕГОСЯ Гусенкова Д.В., Лаинский К.С., научный руководитель доц. Гумеров В.Г. (Самарский государственный технический университет)
Представлено применение импульсного способа для определения гармонической функции скорости жидкости внутри кругового цилиндра, находящегося в плоскопараллельном потоке путем решения задачи Дирихле для круга. Для этого было проведено: краткое повторение известного решения задачи Дирихле для круга, получение краевых условий на поверхности цилиндра и определение гармонических функций скорости жидкости внутри и вне кругового цилиндра. В результате получено, что гармонические функции скорости, полученные с применением решения задачи Дирихле, совпадают с соответствующими скоростями, полученными с применением теории функции комплексного переменного и скорости жидкости от поступательного потока внутри и вне кругового цилиндра в точках, симметричных относительно окружности, равны между собой.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОЛЗУЧЕСТИ Деревянка Е.Е., научный руководитель проф. Радченко В.П. (Самарский государственный технический университет)
Разработан и реализован в виде программного комплекса метод расчёта ползучести и релаксации остаточных напряжений в упрочнённых несимметричных стержневых системах. Стержни системы моделируются в виде сплошных цилиндрических образцов. Приводятся результаты расчётовостаточных напряжений в упрочнённыхстержнях трёхэлементной несимметричной статически неопределимой системы из материала Д16Т при T = 125°C под действием растягивающей нагрузки за расчётное время 500 часов. Полученные расчётные значения кинетики напряжений с течением времени согласуются с предельными асимптотическими значениями, соответствующими стадии установившейся ползучести, что свидетельствует об адекватности разработанной математической модели.
АНАЛИЗ ИДЕНТИФИЦИРУЕМОСТИ СИСТЕМ ЛИНЕЙНЫХ РЕГРЕССИОННЫХ УРАВНЕНИЙ Котенко А.А., научный руководитель инж. Докучаев А.В. (Самарский государственный технический университет)
Дана классификация систем линейных регрессионных уравнений в приложениях с многокритериальным управлением технологическими процессами. В случае взаимодействующих целевых показателей возникает система взаимозависимых регрессионных уравнений. Косвенным МНК дадим корректную постановку задачи идентификации параметров системы, приводящую к состоятельным оценкам параметров управляющих регрессоров. Тогда каждое уравнение системы будет либо точно идентифицируемым (имеется единственная оценка его параметров), либо неидентифицируемым (получено бесконечное множество равноценных оценок, то есть идентифицировать параметры не удалось), либо сверхидентифицируемым (множество алгебраических решений пусто, но двухшаговым МНК однозначно идентифицируются искомые состоятельные оценки). Так выделены случаи, позволяющие определить доверительные интервалы управляющих факторов и в случае взаимосвязанных целевых показателей. ОПРЕДЕЛЕНИЕ КОНТЕКСТА В ЗАДАЧАХ ОБРАБОТКИ ЕСТЕСТВЕННОГО ЯЗЫКА Саксонов Д.С., научный руководитель доц. Шляпкин А.В. (Тольяттинский государственный университет)
Предлагается подход к созданию векторных репрезентаций словпутем применения принципа смысловых сумм слов [1]. Этот принцип предполагается использовать для пар слово-документ. Это позволит смоделировать отношения слов к документам, добавляя вектор документа Используя данный принцип, целевая функция в частном случае с моделью SkipgramNegative-Sampling (SGNS) [1] примет следующий вид:
где БИБЛИОГРАФИЧЕСКИЙСПИСОК: 1. Distributed representations of words and phrases and their compositionality / TomasMikolov, Ilya Sutskever, Kai Chen, Gregory S. Corrado, Jeffrey Dean. // NIPS. – 2013. – P. 3111-3119. 2. Improving neural networks by preventing coadaptation of feature detectors [Электронныйресурс] / Geoffrey E. Hinton, Nitish Srivastava, Alex Krizhevsky, Ilya Sutskever, RuslanSalakhutdinov // arXiv.org. URL: https://arxiv.org/pdf/1207.0580.pdf (дата обращения: 15.04.2018).
3. Tomas Mikolov. Distributed representations of sentences and documents / Tomas Mikolov, Quoc Le // ICML'14. – 2014. – Vol. 32. – P. II-1188-II-1196. ПОЛЬЗОВАТЕЛЬСКИЕ ПРОЦЕДУРЫ МНОГОФУНКЦИОНАЛЬНОГО КОМПЛЕКСА SIMULIAABAQUS ДЛЯ ОПИСАНИЯ Сёмина А.А., научный руководитель доц. Степанова Л.В. (Самарский университет)
Одной из актуальных задач современной механики разрушения является нахождение распределений поврежденности в твердых телах, поскольку реальные элементы конструкций, которые нас окружают, с течением времени обладают свойствами деградирования. Целью данной работы является инкорпорирование тензорной меры поврежденности в расчетную схему конечно-элементного пакета SIMULIAAbaqus, что позволит учесть процесс накопления рассеянных повреждений в твердых телах под нагрузкой. В настоящей работе получены конечно-элементные решения задач для нового материала, описанного с применением процедуры UMAT. Рассмотрены задачи: распределение тензора напряжения в полудиске с вертикальной трещиной под действием сосредоточенной силы без учета накопления повреждений; распределение компонент тензоров напряжения и поврежденностив пластине под действием одноосного растяжения с горизонтальной и наклонной трещиной.
|
|||||||||||||
|
Последнее изменение этой страницы: 2021-05-26; просмотров: 64; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.4 (0.013 с.) |

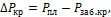
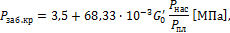
 для всех пар слово-контекст в документе, в то же время сохраняя глобальные отношения между словами, вытекающие из взаимодействия опорных слов
для всех пар слово-контекст в документе, в то же время сохраняя глобальные отношения между словами, вытекающие из взаимодействия опорных слов  и целевых
и целевых  .
.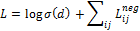
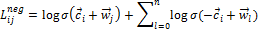
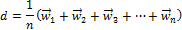
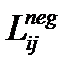 – функция потерь SGNS (2),
– функция потерь SGNS (2), 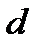 – вектор документов (3) [3].
– вектор документов (3) [3]. – контекстный вектор,
– контекстный вектор, 


