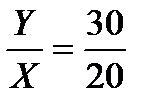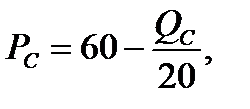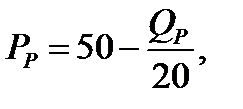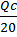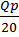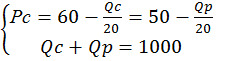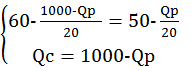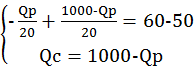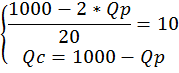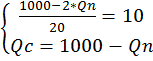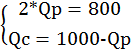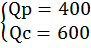Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поведение потребителей в рыночной экономикеСодержание книги
Поиск на нашем сайте
Первый уровень Задача 1. Потребитель тратит весь доход на два товара и потребляет 6 ед. первого товар и 20 ед. второго товара. Цена первого товара в два раза выше цены второго товара. Доход потребителя и цена второго товара удвоились, цена первого товара при этом осталась неизменной. Если потребитель по-прежнему будет потреблять 20 ед. второго товара, то, какое максимальное количество первого товара он сможет себе позволить? Решение. Пусть цена первого товара – х, тогда цена второго – 0,5х. 6х+20×0,5х=6х+10х=16х – первоначальный доход. Цена второго товара увеличилась в 2 раза => 0,5х×2=х. доход также удвоился = 16х×2=32х. Чтобы найти максимальное количество первого товара, который потребитель себе может позволить, нужно: 32х - 20х = 12х. Ответ: 12 единиц.
Второй уровень Задача 2. Функция полезности домохозяйства описывается формулой U(С1,С2) = C1 × С2, где C1 —потребление в текущем году, С2 — потребление в будущем году. Доход домохозяйства в текущем году составляет 20 тыс. долл., а в будущем году он составит 10 тыс. долл. Ставка процента равна 5%. Найдите объем потребительских расходов и сбережений домохозяйства в текущем и будущем году. Как изменится поведение домохозяйства, если ставка процента возрастет до 25%? Решение. Данная задача иллюстрирует проблему межвременных предпочтений (intertemporal choice). В общем виде межвременное бюджетное ограничение запишется: C1 + С2/(1 + i) = I1 + I2/(1 + i), где С1 —потребление в текущем году; С2—потребление в будущем году; I, —доход в текущем году; I2—доход в будущем году; i —ставка процента. Если принять цену текущего потребления за 1, то цена потребления в будущем году (по принципу альтернативной ценности) составит 1/(1 + i). Запишем условие оптимального выбора потребителя (Pc1/Pc2 = MRS — отношение цены текущего потребления к цене потребления будущего года равно предельной норме замены текущего потребления потреблением будущего года) и решим систему из двух уравнений; C1 + C2 /1,05 =20 000 + 10 000/1,05; C2:Ct = 1 + 0,05. Потребление в текущем году составляет приблизительно 14,76 тыс. долл., сбережения 5,24 тыс. долл. В будущем году потребление составит приблизительно 15,5 тыс. долл. Если ставка процента возрастет до 25%, мы увидим, что потребление; в текущем году снижается до 14 тыс. долл., сбережения возрастают до 6 тыс. долл. В будущем году объем потребления составит 17,5 тыс. долл
Третий уровень Задача 3. Потребитель тратит 2000 руб. в день на апельсины и яблоки. Предельная полезность яблок для него равна 2000 — Зх, где х — количество яблок, шт. Предельная полезность апельсина равна 4000 — 5у, где у — количество апельсинов, шт. Цена одного яблока —100 руб., цена одного апельсина-—500 руб. Какое количество яблок и апельсинов купит рациональный потребитель? Решение. 1) В состоянии равновесия отношение предельных полезностей равно отношению цен товаров:
2) Выбор потребителя предопределен бюджетным ограничением: PxX+PyY=l. 3) Поэтому
100х + 500у = 2000. Решая систему уравнений, получаем
100-15(20-5у)=40-5у 100-300+75у=40-5у 100-300+75y-40+5y=0 -200+80y-40=0 80y-240=0 80y=240 y=3 x+15=20 x=5 Ответ: х = 5, у = 3.
Задача 4. Эластичность спроса по цене на концерты для Маши равна 1. Эластичность ее спроса по доходу составляет 3. Перекрестная эластичность по цене между концертами и бассейном равна — 2. В предыдущем году. Маша посетила 100 концертов. В текущем году цена билета на концерт возросла на 15%, цена одного посещения бассейна упала на 5%, а доход Маши возрос на 10%. Какое количество концертов посетит Маша в текущем году? Решение. Эластичность спроса относительно цены рассчитывается как отношениеизменения спроса к изменению цены. EP Δ = где ΔQ- изменение спроса ΔP – изменение цены 1) Δ Qконцертов % = -1 × 15 = -15% 2) Δ Qбассейн % = -2 × 5 = -10% 3) ΔQ% доходов = 3 × 10 = +30% Всего ΔQ%= -15 -10 +30=+5% Qтек.г.= 105 концертов Задача 5. Функция полезности потребителя описывается формулой U = XY/2, где X — объем потребления бананов;Y — объем потребления пепси-колы. Цена 1 кг бананов — 30 руб., 1 л пепси-колы стоит 20 руб. Летом потребитель тратил на эти товары 200 руб. в неделю. Зимой цена бананов поднялась до 50 руб. за 1 кг, цена пепси-колы не изменилась. Определите: а) объем оптимального потребления бананов и пепси-колы летом; б) величину расходов, необходимую зимой для достижения того же уровня полезности, что и летом; в) количественное значение эффекта дохода и эффекта замещения. Решение. а) Поскольку 30X + 20Y = 200, а
то оптимальное потребление составит 3,3 кг бананов и 5 л пепси-колы.
б) Зимой оптимальный потребительский набор составит 2,6 кг бананов и 6,5 л пепси-колы, на его покупку будет затрачено 260 руб. в) Эффект замещения составит 0,7 кг бананов и 1,5 л пепси-колы. Если бы покупатель тратил зимой на покупки 200 руб., то его оптимальный набор составил бы 2 кг бананов и 5 л пепси-колы. Следовательно, эффект дохода составляет 0,6 кг бананов и 1,5 л пепси-колы.
Задача 6. Местный кинотеатр в городе X посещают студенты и пенсионеры. Спрос студентов на услуги кинотеатра описывается уравнением
где Рс — цена билета; Qc — количество билетов, покупаемых студентами. Спрос пенсионеров составляет
Общее число посадочных мест в кинотеатре равно 1000. Какую цену билетов для студентов и для пенсионеров следует назначить кинотеатру, чтобы заполнить зал, если кинотеатр стремится максимизировать прибыль? Решение.
Спрос студентов: Pc=60 - Cпрос пенсионеров: Рр=50 - Q общее = 1000 мест
Решение: если Q=1000, то …
P =50-20=30 P =60-30=30
____________________________Т Е М А 6_____________________________
|
||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 2153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.79.212 (0.009 с.) |

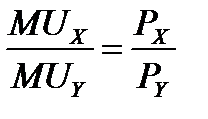
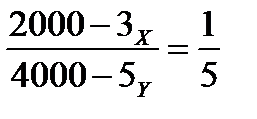
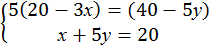
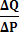 ,
,