Тема 2. 4. Геометрические характеристики плоских сечений(4. 4. – авто)

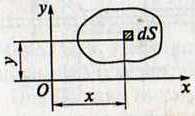
(эзс – 2 час, арх – 1 час, авто – 1)

Моменты инерции сечений

1. Статический момент инерции - алгебраическая сумма произведений элементарных площадей на координаты их центров тяжести – мм³ , см³, м³

(сумма d S ∙ х илиd S ∙ у)

 

 

а) в интегральной форме

 

S_х = ∫ уdS - статический момент инерции относительно оси х

 S_у = ∫ хdS- статический момент инерции относительно оси у

 

б) по формулам статики  S_х = Sy_с       S_у = Sх_с

S – площадь сечения 

y_с и х_с – координаты центра тяжести сечения

 

в) если ось х проходит через центр тяжести сечения → y_с = 0→ S_х = Sy_с = S∙0 = 0

г) статические моменты сечения относительно центральных осей равны нулю (центральные оси – проходят через центр тяжести сечения – так как y_с = 0 и х_с = 0)

 

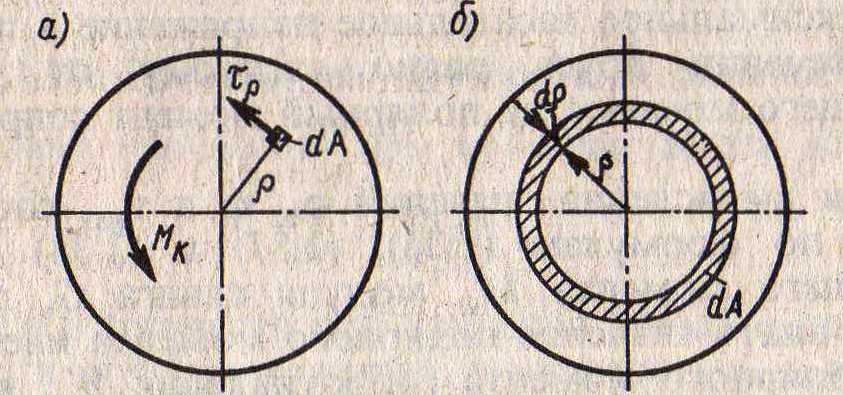
2. Полярный момент инерции - сумма произведений площадей элементарных площадок поперечного сечения на квадраты их расстояний от центра (для круглого сечения – мм⁴ , см⁴, м⁴)

 

J_р = ∫p²dS

S

 

 

р – расстояние от центра до центра тяжести элементарной площадки.

 

 

3. Осевые моменты инерции относительно координатных осей х и у.

а) представим, что сечение разделено на множество элементарных площадок dS

 

 

б) координаты элементарной площадки х и у.

в) тогда интегралы

 

J_х = ∫у²dS   и                  J_у = ∫х²dS

                                                            S                                                               S

называются моментами инерции сечения относительно осей х или у

 

4. Центробежные моменты инерции относительно координатных осей х и у.

 

J_ху = ∫хуdS

                                                                                               S

5. Связь между осевыми моментами инерции относительно парал­лельных осей

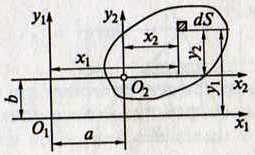
а) введём две системы координат О₁х₁у₁ и О₂х₂у₂ – оси которых попарно параллельны и находятся на расстоянии а и b

б) система О₂х₂у₂ – связана с телом

в) х₂ = х₁ – а           у₂ = у₁ – b           

г) определение статического момента сечения относительно оси х₂

 

S_х2 = ∫(у₁ – b)dS = ∫у₁dS - ∫bdS 

                                                                                               _{S                                         S                S}

 

S_х2 = S_х1 - bS

 

 

д) определение статического момента сечения относительно оси у₂

 

S_у2 = ∫(х₁ – а)dS = ∫х₁dS - ∫аdS 

                                                                                               _{S                                         S                S}

 

S_у2 = S_у1 - аS

 

Вывод: при параллельном переносе осей статический момент меняется на величину, равную произведению площади S на расстояние между ними (осями)

 

6. Всегда можно (единственный вариант) подобрать оси так, чтобы

А) S_х1 – bS = 0- (центр тяжести лежит на оси х₁→ у₁ = 0, b = 0→ S_х1= ∫у₁dS = 0→ bS = 0

                                                                                       s

 

Б). S_у1 - аS= 0

 (центр тяжести лежит на оси у₁→ х₁ = 0, а = 0→ S_у1= ∫х₁dS = 0→ аS = 0

 

 

7. Вывод:

А) центральная ось - ось, относительно которой статический момент равен нулю.

Б) центр тяжести сечения – точка пересечения центральных осей

В) статический момент относительно всякой оси, проходящей через центр тяжести, равен нулю.

 

8. Расстояние до центральных осей от произвольно взятых определяется зависимостями

Из   S_х = Sy_с       S_у = Sх_с     → Ус = S_х1\S            Xс = S_у1\S

 

 

10. Понятие о главных центральных моментах инерции

 

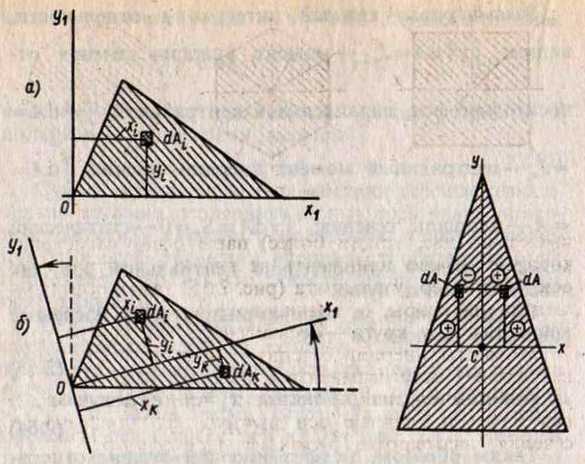
А) главные оси – оси, относительно которых осевые моменты инерции принимают экстремальные значения, а центробежный момент равен нулю.

Б) практическое значение имеют не любые главные оси, а только главные центральные оси (через центр тяжести)

В) сечение с двумя осями сим метрии (например, прямоугольник) имеет две главные центральные оси симметрии (центральные → проходят через центр тяжести, главные →

- по одну сторону от оси площадка dS (dA) с элементарным моментом инерции + хуdA (так же, как у треугольника)

- по другую сторону от - хуdA

- при суммировании их по всему сечению Jху = 0

- осевые моменты сечения экстремальные: относительно оси у  - произведение площади на координату х)

Г) у квадрата две пары две пары центральных главных осей

Д) у правильного шестиугольника три пары центральных главных осей

Е) у круга – бесчисленное множество пар

 

 

 

Ж) главные центральные моменты инерции – моменты инерции сечения относительно главных центральных осей.

З) главные плоскости – плоскости, проведённые через ось бруса и главные оси инерции его поперечного сечения.

 

 

 

Самостоятельная работа обучающихся (эзс – 2 час, арх – 4 час, авто – 2)

1. Заполнить таблицу основных геометрических характеристик для наиболее

распространенных форм сечений и вложить их в «Приложения».

2. Решить задачи по определению центра тяжести и геометрических характеристик сложных фигур

1. Решение задач на определение главных центральных момен­тов инерции составных сечений, имеющих ось симметрии - авто