
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. 2. Растяжение и сжатие (4. 2. – авто)Содержание книги
Поиск на нашем сайте
(эзс – 4 час, арх – 2 час, авто – 2) Понятие о сжатии и растяжении 1. Растяжение – вид нагружения, при котором в поперечном сечении бруса (стержня) возникают только нормальные силы, а прочие внутренние силовые факторы равны нулю: нормальная сила 2. Сжатие отличается от растяжения только знаком силы и нормальная сила 3. С жатие, сопровождаемое изгибом – для длинных тонких стержней.
Закон Гука 1. Закон Гука определяет линейную зависимость между напряжением σ и деформацией ε (какова сила, такова и деформация) σ = Е ε
2. Е – модуль упругости 1 рода, определяется экспериментально (в таблицах)
3. Для однородного тонкого стержня длиной l деформация ε ε = ∆ l\ l
∆ l – удлинение стержня под действием приложенной силы ε – деформация (относительное удлинение)
Удлинение стержня 1. Деформация – сумма силовой и температурной деформации ε = σ\Е + αt
α – коэффициент температурного расширения материала t - температура 2. Деформация для однородного стержня, нагруженного по концам и равномерно нагретого
∆l = Nl\ЕS + αlt
Построение эпюр (графиков)
1. Эпюра нормальных сил – график изменения нормальной силы стержня вдоль его оси 2. Эпюра напряжений – график изменения напряжений стержня вдоль его оси 3. Эпюра перемещений – график перемещений стержня вдоль его оси Вывод: эпюры нужны для наглядности представления о законах изменения исследуемых величин
Диаграмма растяжения
1. Образец из низкоуглеродистой стали – диаграмма для образца 2. Диаграмма – в координатах F, l∆ 3. Четыре зоны на диаграмме: А) зона упругости – материал работает по закону Гука (для наглядности – отступление от масштаба) – удлинения малы и ОА почти совпадала бы с осью F
Б) зона общей текучести (площадка текучести) – существенное изменение длины образца без заметного увеличения нагрузки (не у всех металлов – у Al, легированных сталей нет)
В) зона упрочнения – удлинение сопровождается возрастанием нагрузки. - Здесь намечается место будущего разрыва шейка – местное сужен ие образца.
Г) зона местной текучести - от точки С сила уменьшается, но образец удлиняется - шейка прогрессирует - удлинение носит местный характер
Д) точка Д - разрушение образца Относительная поперечная деформация. Коэффициент Пуассона.
1. Рассматриваем растяжение (сжатие) прямого бруса 2. Брус испытывает как продольные, так и поперечные деформации 3. Удлинение - ∆l, уменьшение ширины бруса на ∆b 4. Относительная продольная деформация ε = ∆ l\ l 5. Относительная поперечная деформация ε1 = ∆ b\ b 6. Коэффициент Пуассона – отношение относительной поперечной деформации к относительной продольной деформации (характеризует физические свойства материала: для сталей от 0,25 до 0,35 – таблица)
µ = ε1\ ε
Основные механические характеристики материалов
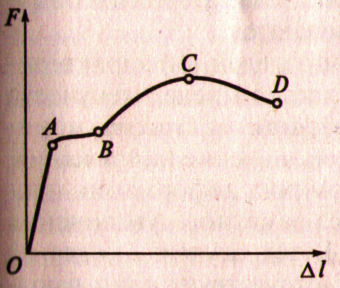
1. Перестроим диаграмму растяжения в координатах – диаграмма для материала: А) вместо F – σ. Сила F приложена к образцу, напряжение зависит от размера образца σ = N\S Б) вместо ∆l – ε. ∆l – просто удлинение, а ∆l – зависит от длины образца ε = ∆ l\ l
2. Характерные точки: А) Предел пропорциональности σп – наибольшее значение напряжения, до которого материал следует закону Гука. Б) Предел упругости σу – наибольшее значение напряжения, до которого материал не получает остаточных деформаций (восстанавливается)
3. Предел текучести σт.р. – значение напряжения, при котором рост деформации происходит без заметного увеличения нагрузки. (σт.р – т екучести на р астяжение σт.с – т екучести на с жатие,) Прим. При отсутствии явной площадки текучести принимают напряжение, при котором ос таточная деформация 0,2 % - σ0,2 – условный предел текучести)
4. Предел прочности (Временное сопротивление разрыву σв.р., σв.сж – временное сопротивление сжатию). σв.р., σв.сж являются сравнительными характеристиками прочностных свойств материала и часто используется при расчётах. Прим. При этом значении материал не разрушается. Фактическое напряжение будет больше, так как площадь поперечного сечения за счёт шейки меньше (σ = N\S 5. Относительное удлинение при разрыве (при испытаниях на растяжение) – средняя остаточная деформация к моменту разрыва на определённой стандартной длине образца l0 = 10d, l0 = 5d, d – диаметр образца. Расчёты на прочность при растяжении и сжатии 1. Размеры конструкций должны обеспечивать их прочность при наименьших затратах материала.
2. Выявляется точка конструкции с наибольшим напряжением – σнаиб
3. σнаиб должно быть меньше допустимого значения напряжения [σ]
4. Коэффициент запаса n задают при проектировании А) n Т = 1,5…2 для пластичного материала - от предела текучести Б) nв = 2,5…4 для хрупкого материала - от предела прочности В) nв = 2…5 для проектирования строительных сооружений на долгий срок эксплуатации.
5. Допускаемое напряжение А) для пластичных материалов [σ] = σт.\nТ Б) для хрупких материалов [σ] = σв.\nв
6. Условие, из которого определяют размеры проектируемого элемента
σнаиб
σнаиб = N\S
Самостоятельная работа обучающихся (эзс – 4 час, арх – 6 час, авто – 2) 1. Построить эпюры продольных сил, нормальных напряжений и перемещений для ступенчатого бруса по вариантам 2. Решить задачи на проверку прочности и подбор сечения по вариантам 3. Составить глоссарий основных понятий по теме «Растяжение и сжатие» 1. Расчётно-графическая работа на построение эпюр продольных сил, напряжений, перемещений сечений бруса, определение коэффициента запаса прочности - авто
|
||||
|
Последнее изменение этой страницы: 2021-04-13; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.129.8 (0.009 с.) |

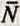 направлена от сечения
направлена от сечения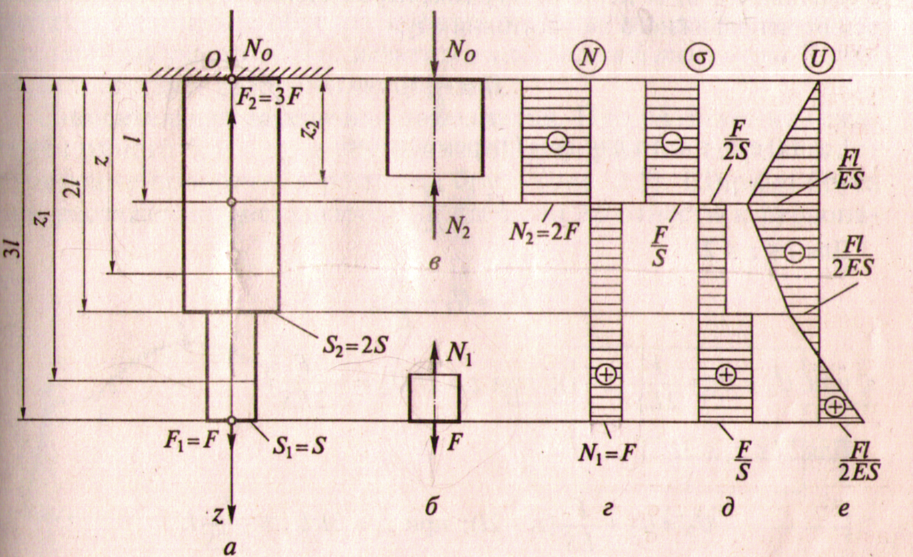

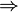 S меньше – σ будет больше)
S меньше – σ будет больше)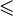 [σ]
[σ]


