С использованием векторных операций

n=input('введите n=');

i=1:n;

s=sum(1./i.^2);

disp(strcat('s=', num2str(s)))

 

Задача 12. Нахождение суммы

Условие задачи. Дано положительное число х. Вычислить значение суммы.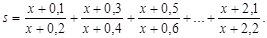

Проанализируем задачу вычисления суммы и выведем закономерность изменения слагаемого, то есть получим общую формулу для его вычисления. В формуле числителя есть величина, которая принимает значения 0.1; 0.3; 0.5; … 2.1, назовем ее у. Так как слагаемое в знаменателе больше, чем в числителе на 0.1, то общая формула слагаемого получится следующей: 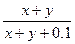. Каждое новое слагаемое будет получаться по этой формуле при увеличении значения у на 0.2, начиная с у= 0.1.

Как и в предыдущей задаче, для получения суммы каких либо слагаемых используется следующий метод. Сначала задаем переменной s, хранящей значение суммы, значение, равное нулю. Далее последовательно прибавляем к сумме по одному слагаемому, и результат сложения присваиваем той же самой переменной s.

Исходным данным в этой задаче является вещественное число х. Результатом будет сумма слагаемых s. При вводе х надо контролировать его значение, чтобы оно соответствовало заданному условию x >0. Для этого ввод надо выполнять в цикле до тех пор, пока х не станет больше нуля. Если значение х сразу будет введено положительным, то цикл выполнится один раз, если же будет введено неположительное значение, то ввод будет повторяться. Для нахождения суммы надо повторять действие суммирования s = s +<слагаемое> и действие, изменяющее значение у для следующего слагаемого. Для повторения этих действий можно использовать арифметический цикл, предварительно вычислив число повторений, так как число слагаемых явно не задано, но может быть определено, а можно воспользоваться циклом с заранее неизвестным числом повторений (итерационным). Воспользуемся вторым способом. Суммирование слагаемых должно начинаться для у =0.1 и продолжаться до у = 2.1 с шагом 0.2. Но так как вещественные числа в памяти компьютера представляются приближенно, то при сложении таких чисел накапливается ошибка, поэтому результат вычисления у = у +0.2 будет не точным, и проверку вещественного числа y на строгое равенство конечному значению выполнять нельзя. Для того, чтобы не потерять последнюю итерацию цикла, возьмем граничное значение для величины у не 2.1, а 2.15.

До цикла необходимо задать начальное значение у =0.1 и начальное значение суммы s =0. В теле цикла к сумме прибавляется слагаемое 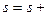 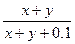и изменяется величина у: у = у +0.2. По окончании суммирования результат (значение суммы) выводится на экран.